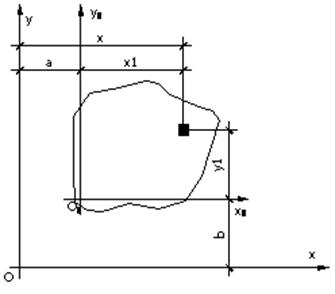
Пусть известны и Ix, Iy, Ixy. Параллельно осям хy проведем новую ось x1, y1.
И определим момент инерции того же сечения относительно новых осей.
X1= x-a; y1=y-b
I x1= ∫ y1 dA = ∫ (y-b)2 dA = ∫ (y2- 2by + b3)dA = ∫ y2 dA – 2b ∫ ydA + b2 ∫dA=
=Ix – 2b Sx + b2A.
Если ось x проходит через центр тяжести сечения, то статический момент Sx =0.
I x1= Ix + b2A
Аналогично новой оси y1 будем иметь формулу I y1= Iy + a2A
Центробежный момент инерции относительно новых осей
Ix1y1= Ixy – b Sx –a Sy + abA.
Если оси xy проходят через центр тяжести сечения, то Ix1y1= Ixy + abA
Если сечение симметрично, хотя бы одна из центральных осей совпадает с осью симметрии, то Ixy =0 , а значит Ix1y1= abA
Изменение моментов инерции при повороте осей.
Пусть известны осевые моменты инерции относительно осей xy.
Новую систему координат xy получим путем поворота старой системы на угол (a >0), если поворот против часовой стрелки.

Установим зависимость между старыми и новыми координатами площадки
y1 =ab = ac – bc = ab- de
из треугольника acd:
ac/ad =cos α ac= ad*cos α
из треугольника oed:
de/od =sin α dc = od*sin α
Подставим эти значения в выражение для y
y1 = ad cos α - od sin α = y cos α - x sin α.
Аналогично
x1 = x cos α + y sin α.
Вычислим осевой момент инерции относительно новой оси x1
Ix1 = ∫y12 dA = ∫ (y cos α - x sin α)2dA= ∫ (y2 cos2 α - 2xy sin α cos α + x2 sin2 α)dA= =cos2 α ∫ y2 dA – sin2 α ∫xy dA + sin2 α ∫x2 dA = Ix cos2 α - Ixy sin2 α + Iy sin2 α.
Аналогично Iy1 = Ix sin2 α - Ixy sin2 α + Iy cos2 α .
Сложим левые и правые части полученных выражений:
Ix1 + Iy1 = Ix (sin2 α + cos2 α) + Iy (sin2 α + cos2 α) + Ixy (sin2 α - cos2 α).
Вывод:
Ix1 + Iy1 = Ix + Iy
Сумма осевых моментов инерции при повороте не меняется.
Определим центробежный момент инерции относительно новых осей. Представим значения x1 ,y1 .
Ix1y1 = ∫x1 y1 dA = (Ix – Iy)/2*sin 2 α + Ixy cos 2 α.
Главные моменты и главные оси инерции.
Главными моментами инерции называют их экстремальные значения.
Оси, относительно которых получены экстремальные значения называются главными осями инерции. Они всегда взаимно перпендикулярны.
Центробежный момент инерции относительно главных осей всегда равен 0. Так как известно, что в сечении есть ось симметрии, то центробежный момент равен 0, значит ось симметрии является главной осью. Если взять первую производную от выражения I x1 , затем приравнять её к “0”, то получим значение угла = соответствующего положению главных осей инерции.
tg2 α0 = - 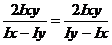
Если α0 >0,то для определенного положения главных осей старую ось нужно повернуть против хода часовой стрелки. Одна из главных осей является max, а другая – min. При этом ось max всегда соответствует меньший угол с той случайной, осью относительно которой имеет больший осевой момент инерции. Экстремальные значения осевого момента инерции определяется по формуле:
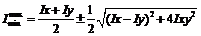
Глава 2. Основные понятия сопротивления материалов. Задачи и методы.
При проектировании различных сооружений нужно решать различные вопросы прочности, жесткости, устойчивости.
Прочность – способность данного тела выдерживать различные нагрузки без разрушения.
Жесткость – способность конструкции воспринимать нагрузки без больших деформаций (перемещений). Предварительно допустимые значения деформации регламентируют строительные нормы и правила (СНИП).
Устойчивость
Рассмотрим сжатие гибкого стержня

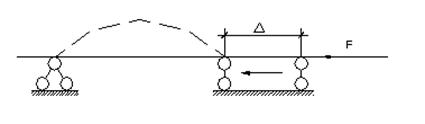
Если нагрузку постепенно увеличивать, то сначала будет происходить укорочение стержня. При достижении силой F некоторой критической величины произойдет выпучивание стержня. - абсолютное укорочение.
При этом стержень не разрушается, но резко изменяет свою форму. Такое явление называется потерей устойчивости и приводит к разрушению.
Сопромат – это основы наук о прочности, жесткости, устойчивости инженерных конструкций. В сопромате используются методы теоретической механики, физики, математики. В отличии от теоретической механики сопромат учитывает изменение размеров и формы тел под действием нагрузки и температуры.






