1. Постановка задачи
2. Выбрать рациональное условие равновесия сумма m =0
3. На основании рационального условия составить и решить уравнения равновесия.
- Va -?
- Сумма m =0
- Va *5 – 10 *3 =0
4. Нанести величину реакции на расчетную схему.
V -? Σ ma =0 - VB * 5 + 10 * 2 =0 VB = 4 кН
Если результат меньше 0, то нужно:
| 1. Изменить на расчетной схеме предположенное направление реакции на противоположное. 2. Указать величину со знаком “+”. После определения всех реакций опор делают проверку, для которой при – меняют условия равновесия и исп-ая при вычислении реакции опор. | 
|
| y = 6 –10 + 4 = 10 – 10 = 0 Допустимая погрешность < 0,1 % Пример №3 Va -?; Σ mB=0 Va * 6 – 4 * 6 * 3 = 0; Va = 12 кН VB -? Σ ma=0 - VB * 6 + 4 * 6 * 3 = 0 VB = 12 кН Проверка: ΣY=12-4*6+12=24-24=0 | 
|
Определение реакции опоры консоли
| В общем случае в заделке консоли возникает три реакции: Va, Ha, Ma. Определим эти реакции. Va -?; Σ y =0 Va – F sin α =0 Va = F sin α Ha -?; Σ x =0 Ha – F cos α =0 Ha = F cos α Ma -?; Σ ma=0 - Ma + F sin α * a = 0 Ma = a F sin α* a | 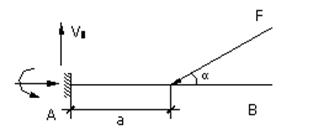
|

| Va -?; Σy = 0 Va – 10 = 0, Va = -10кН Ma -?; Σma=0 - Ma – 4 + 10 *5 = 0 Ma= 54 кН |
Часть 2. Сопротивление материалов.
Лекция 3.
Основные понятия сопротивления материалов.
Глава 1. Геометрические характеристики сечений.
Мысленно рассечём твердое тело плоскостью перпендикулярно его продольной оси. Такое сечение называется поперечным. Поперечное сечение можно рассматривать как плоское тело (например, пластина) имеющая
| бесконечно малую толщину. Точка О – пересечение продольной оси с секущей плоскостью совпадает с цент- ром тяжести сечения. Характеристики поперечного сечения: площадь –“А”, статический момент –“S”, момент инерции “I”, момент сопротивле- ния “W”. Эти характеристики необходи- мы для расчета конструкции на проч- ность, жесткость и устойчивость. Статические моменты сечений. | 
|

| Дано плоское сечение произвольной формы, площадь которой “А”. Поместим его в прямоугольную систему координат. Выделим бесконечно малую площадку А равную dA. Полагаем, что все сечение состоит из бесчислен- ного множества элементарных площадок dA, тогда А всего сече- ние будет А = dA. Пусть центр тяжести элементарной площадки имеет координаты х и y, тогда статическим моментом всего сечения относительно оси х – будет выражение Sx = ∫ y dA, Sy = ∫ x dA. |
Размерность статического момента [ м3] [см3].
Статический момент сложного сечения (т. е. сечения состоящего из нескольких простых фигур), относительно какой – либо оси равно сумме статических моментов составляющих сечения частей (фигур) относительно той же оси. Статический момент может быть числом положительным, отрицательным или нулевым. Параллельно оси х проведем ось х1. положение новых (х1 y1) осей относительно старых (х y) известно, т. е. известны расстояния между осями. Координаты площадки dA в новых осях х1 ; y1 . Составим выражение статических моментов отонсительно новых осей
Sx = ∫ y1 dA = ∫ (y –b) dA= ∫ y dA – b
Sx1 = Sx – bA
Аналогично относительно оси y1: Sy1 = Sy – aA.
Найдём такое положение осей х1; y1 когда статические моменты относительно этих осей обратятся в нуль. При этом координаты новых осей обозначим xc и yc.
Sx1 = Sx – bA = 0 b=yc
Sx – yc A = 0 yc = Sx / А.
Аналогично xc = Sy / А. (1)
Точка С – центр тяжести всего сечения. Если через эту точку провести произвольную ось, то она будет называться центральной. Если центр тяжести заранее известен, то можно вычислить статические моменты.
Sx = yc A
Sy = xc A (2)
Определение центра тяжести поперечного сечения является важной задачей любых прочностных расчетов.
Алгоритм определение центра тяжести сложного сечения:
1. Разбить сложное сечение на простые фигуры и пронумеровать их.
2. Выбрать случайные координатные оси x, y. (лучше, если все сечение будет в одной четверти).
3. Определим площади и положения центра тяжести каждой фигуры.
4. Найти площадь всего сечения.
5. По формуле (2) вычислить статические моменты каждой фигуры.
6. Определить суммарные статические моменты.
7. По формуле (1) вычислить координаты центра тяжести всего сечения.
Пример: Определить центр тяжести сложного сечения.
| Размеры в мм. А1 = 20 * 20 = 400 А1 = 20 * 40 = 800 А = А1+ А2 = 400 + 800 = 1200 Статические моменты каждой фигуры относительно оси х, y относительно оси х первой (1) фигуры Sx(1)= А1 yc1 = 400 * 30 = 12 * 103 Sx(1)= А2 yc2 = 800 * 10 = 8 * 103 Sy(1)= А1 xc1 = 400 * 10 = 4 * 103 Sy(2)= А2 xc2 = 800 * 20 = 16 * 103 | 
|
| Суммарные статические моменты Sx(1)= Sx(1) + Sx(2) = (12 +8) * 103 = 20 * 103 Sy(1)= Sy(1) + Sy(2) = (4 +16) * 103 = 20 * 103 Вычисление координат центра тяжести всего сечения xc = Sy / А = 20 * 103 / 1200 = 16,7 xc = Sy / А = 20 * 103 / 1200 = 16,7 | 
|
Моменты инерции сечений.
Осевые моменты инерции относительно х, y
соответственно Ix = ∫ y2 dA
Iy = ∫ x2 dA
Полярный момент инерции относительно
точки О Ip = ∫ p2 dA
Центробежный момент инерции относительно х, y
Ixy = ∫ xy dA
Зависимость между осевыми и полярными моментами инерции
Ix + Iy = Ip [м4], [см4]
p всегда положительны, x и y может быть любыми числами.
Ixy относительно осей, хотя бы одна из которых, совпадает с осью симметрии сечения равна нулю. Осевой момент инерции сложного сечения относительно произвольной оси равна сумме осевых моментов состоящих сечения частей относительно той же оси.
Пример: определить осевые моменты инерции прямоугольника со сторонами b и h, относительно его центральных осей.
Отделим прямыми линиями параллельными оси х элементарную площадку dA равную b dy. В соответствии с формулой:
| Ix = ∫ y2 dA = ∫ y2 b dy = b ∫ y2 dy = b y3/3 = = b ((h3/ 23 3) + (h3/ 23 3)) => Ix= bh3 / 12. Iy = b3 h / 12 Вывод: в куб возводят ту сторону прямоугольника, которая перпендикулярна рассмотренной оси. Осевой момент треугольника относительно центральной оси параллельной основанию Ix = bh3 / 36 Осевые и полярные моменты инерции для круга Ix = Iy = п d4 / 64 = 0,05 d4 Полярный момент инерции Ip = п d4 / 32 = 0,1 d4 | 

|






