Так как пластина имеет вертикальную ось симметрии, то центр тяжести находится на этой оси.

Xc =0; Yc --?Yc = 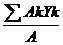, где

Yk – ординаты центра тяжести отдельных частей пластины.

Разобьём пластину на две части (два прямоугольника), тогда y₁ =15 мм,    y =31см.

А₁ =1 * 30 = 30 см²           А₂ = 10 * 2 = 20 см²   А = А₁ + А₂ = 20+ 30= 50

 

y₁ =                           y_C = = 21.4 см

 

Центр тяжести треугольника лежит в точке пересечения медиан. Медианы делятся центром тяжести в отношении 2:1. Нетрудно доказать, что центр тяжести прямоугольного треугольника расположен на расстоянии две трети катета от острого угла и одной трети катета от прямоугольного угла.

 

         Определение реакций опор простой балки.

 

Условие равновесия исполняется при определённой реакции опор в различных конструкциях и сооружениях.

Простая балка – брус, опирающийся на две опоры, одна из которых шарнирно неподвижная, а другая шарнирно подвижная.

 

нагрузка Р [кН/м² ]

 

Расстояние между опорами балки называется пролёт.

При расчете пользуются не реальной схемой сооружения, а расчётной схемой. Расчётная схема – упрощенное, идеализированное изображение сооружения и опор. На расчетной схеме балка показывается одной линией, проходящей через центр тяжести поперечных сечений.

Шарнирно неподвижная опора обозначается                  , а подвижная                 .

Если к балке приложена нагрузка в виде, например, равномерно насыпанного песка, слоем определенной толщины, то мы получим равномерно распределённую по площади (=А=а*в) нагрузку. Мерой её воздействия является интенсивность “р”, имеющая размерность силы на единицу площади.

Так как в расчётной схеме вместо реальной балки использована линия, то распределённую по площади нагрузку нужно привести к линии. Для этого интенсивность умножают на ширину распределённой нагрузки q = p в. Размерность [кН/Пм ]. Равнодействующая нагрузки q расположена посередине участка длиной ”a” и R = q a [кН]. Если длина участка ”a” достаточно мала, то можно равномерно распределённую нагрузку заменить сосредоточенной силой. Это упрощает расчет, но делает его менее точным.

Кроме распределённой и сосредоточенной нагрузок может быть нагрузка в виде сосредоточенного момента, который является результатом действия пары сил, момент которой m [кН/м ].

При определении реакции опор приходится вычислять момент распределённой нагрузки.

Правило определения момента распределённой нагрузки.

 

Найти равнодействующую R= q a. Она приложена посередине участка a”.

 

1. Найти её плечо h, которое равно перпендикуляру, опущенного из точки на линию действия R.
2. Определить по направлению вращения силой R знак момента ‘+’ по ходу часовой стрелки.
3.  Вычислить произведение + q ah

 

Пример:

Определить момент распределённой нагрузки на точку О

                                         m₀ =?

                                                       m₀ = 10 * 4 * 8

                     m₀ = 320 кН м

 

Определить реакции опор балки

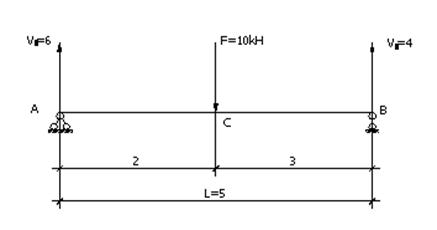
После изображения заданной нагрузки на расчётную схему наносят реакции опор.

Направление реакции зависит от реакции опоры и направления нагрузок. Так шарнирно неподвижной опоре в общем случае направление реакции произвольно и она может быть разложена по двум направлениям – горизонтальном и вертикальном. Тогда эту реакцию заменяют двумя: горизонтальной На и вертикальной Va.

       Частный случай.

Если заданные нагрузки вертикальные, то На =0.

В шарнирно подвижной опоре реакция всегда совпадает с направлением опорного стержня.