Доверительная область простой линейной регрессии

Для линейной регрессии у = а +bх доверительная область (с доверительной вероятностью α) на заданном отрезке будет ограничена гиперболами [12]:

(4.87)

где

(4.88)

(4.89)

(4.90)

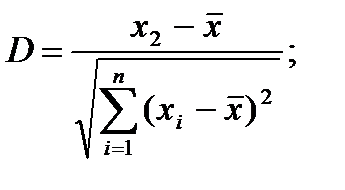(4.91)

(4.92)

Значения коэффициента u(ν, α, λ) приведены в таблице 4.18, 4.19. Доверительная зона, рассчитанная по приведенным выше соотношениям, является геометрическим местом доверительных интервалов для различных значений х.

Таблица 4.18

Коэффициенты u (ν, α, λ) для построения доверительной области линейной регрессии [12] при λ=0-0,45

ν	λ
ν	0	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,45
α = 0,95
1	12,700	13,320	13,920	14,480	15,010	15,520	16,000	16,460	16,890	17,290
2	4,303	4,445	4,582	4,715	4,844	4,968	5,087	5,202	5,312	5,417
3	3,182	3,271	3,356	3,438	3,518	3,594	3,668	3,740	3,809	3,875
4	2,776	2,847	2,915	2,978	3,040	3,101	3,159	3,215	3,270	3,332
5	2,571	2,633	2,692	2,748	2,802	2,854	2,904	2,953	3,000	3,045
6	2,447	2,504	2,558	2,609	2,659	2,706	2,751	2,795	2,838	2,879
7	2,365	2,418	2,469	2,517	2,563	2,607	2,650	2,691	2,730	2,769
8	2,306	2,357	2,406	2,452	2,496	2,538	2,578	2,616	2,654	2,690
9	2,262	2,312	2,358	2,403	2,445	2,485	2,524	2,561	2,597	2,632
10	2,228	2,277	2,322	2,365	2,406	2,445	2,482	2,518	2,552	2,586
11	2,201	2,249	2,293	2,335	2,375	2,413	2,449	2,484	2,517	2,500
12	2,179	2,226	2,269	2,311	2,350	2,387	2,422	2,456	2,489	2,521
13	2,160	2,207	2,250	2,290	2,329	2,365	2,400	2,433	2,466	2,497
14	2,145	2,191	2,233	2,273	2,331	2,347	2,381	2,414	2,446	2,476
15	2,132	2,177	2,219	2,258	2,295	2,331	2,365	2,397	2,429	2,459
16	2,120	2,165	2,200	2,245	2,282	2,317	2,351	2,383	2,414	2,444
17	2,110	2,154	2,195	2,234	2,271	2,305	2,338	2,370	2,401	2,431
18	2,101	2,145	2,186	2,224	2,260	2,295	2,328	2,359	2,389	2,419
19	2,093	2,137	2,177	2,215	2,251	2,285	2,318	2,349	2,379	2,408

Окончание таблицы 4.18

ν	λ
ν	0	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,45
α = 0,95
20	2,086	2,129	2,170	2,207	2,243	2,277	2,309	2,340	2,370	2,399
25	2,060	2,102	2,141	2,178	2,213	2,246	2,277	2,307	2,336	2,364
50	2,009	2,049	2,086	2,121	2,154	2,186	2,215	2,244	2,271	2,297
100	1,984	2,023	2,060	2,094	2,126	2,157	2,186	2,213	2,240	0,265
∞	1,960	1,998	2,034	2,068	2,099	2,128	2,156	2,183	2,209	2,234

Таблица 4.19

Коэффициенты u (ν, α, λ) для построения доверительной области линейной регрессии [12] при λ=0,5-0,95

ν	λ
ν	0,5	0,55	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95
α = 0,95
1	17,670	10,025	18,355	18,661	18,941	19,195	19,422	19,619	19,782	19,907
2	5,517	5,612	5,701	5,785	5,864	5,935	6,000	6,058	6,107	6,144
3	3,939	4,000	4,059	4,114	4,166	4,214	4,258	4,297	4,330	4,356
4	3,373	3,422	3,469	3,514	3,556	3,596	3,632	3,664	3,692	3,714
5	3,089	3,132	3,173	3,212	3,249	3,284	3,316	3,345	3,371	3,390
6	2,919	2,958	2,995	3,031	3,065	3,097	3,127	3,154	3,178	3,197
7	2,806	2,842	2,877	2,911	2,943	2,974	3,002	3,028	3,051	3,068
8	2,726	2,760	2,793	2,826	2,856	2,886	2,913	2,938	2,959	2,976
9	2,666	2,699	2,731	2,762	2,792	2,820	2,846	2,870	2,891	2,908
10	2,618	2,650	2,681	2712	2,741	2,768	2,794	2,818	2,838	2,855
11	2,582	2,613	2,643	2,673	2,701	2,728	2,753	2,777	2,797	2,813
12	2,552	2,582	2,612	2,641	2,669	2,695	2,720	2,743	2,763	2,779
13	2,527	2,557	2,586	2,614	2,642	2,668	2,692	2,715	2,734	2,750
14	2,506	2,536	2,564	2,592	2,619	2,645	2,669	2,691	2,710	2,726
15	2,488	2,517	2,545	2,573	2,599	2,625	2,649	2,671	2,690	2,706
16	2,473	2,501	2,529	2,556	2,583	2,608	2,631	2,653	2,672	2,688
17	2,459	2,487	2,515	2,542	2,568	2,593	2,616	2,638	2,657	2,672
18	2,447	2,475	2,502	2,529	2,555	2,579	2,603	2,624	2,643	2,658
19	2,437	2,464	2,491	2,518	2,543	2,568	2,591	2,612	2,631	2,646
20	2,427	2,455	2,481	2,508	2,533	2,577	2,580	2,601	2,620	2,635
25	2,392	2,418	2,444	2,470	2,494	2,518	2,540	2,561	2,579	2,594
50	2,323	2,348	2,372	2,396	2,419	2,442	2,463	2,483	2,501	2,515
100	2,290	2,314	2,338	2,361	2,384	2,405	2,426	2,446	2,463	2,248
∞	2,258	2,281	2,304	2,327	2,349	2,370	2,390	2,409	2,426	2,440

Пример [12]: по данным представленным ниже построить 95%-ю доверительную зону для регрессии на интервале от х₁=3 до х₂=10 и доверительный интервал для при x_i=5,1 ().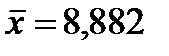

x_i1,2 2,7 3,9 5,1 7,2 9,4 11,1 12,4 16,1 19,1

y_i 3,1 6,1 12,1 21,3 27,4 31,2 41,1 51,2 71,1 91,2

4,1 8,4 16,1 19,4 21,5 36,4 38,2 48,1 59,2 81,2

5,6 9,2 9,3 18,1 19,8 27,3 31,4 31,4 63,5 79,4

4,27 7,9 12,5 19,6 22,9 31,36 36,9 43,56 64,6 83,93

Уравнение регрессии имеет вид (расчетные формулы см. раздел 4.3):

Далее имеем:

Из таблицы 4.18 для v=8, α=0,95 и λ=0,566 находим (интерполяцией) u(8;0,95;0,566)=2,78.

Доверительная зона для регрессии имеет вид:

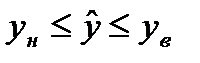, где

Для значений границы доверительной зоны будут равны (подставляем x=5,1 в уравнение гиперболы):

ДВУХФАКТОРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Ранее рассматривались методы оценки и анализа линейной регрессии y=f(x). Если случайная величина у может зависеть одновременно от двух и более переменных, возникает задача оценки и анализа множественной регрессии:

y=f(x₁,x₂,…,x_k), (4.93)

где x_j (j-1,2,…,k) –независимые переменные.

Рассмотрим в качестве примера [12] регрессию y=α+β₁x₁+ β₂x₂для случая двух независимых переменных x₁ и x₂. Для большего числа переменных оценки могут быть получены по аналогии. Для данного случая коэффициенты в уравнении регрессии определяются следующим образом:

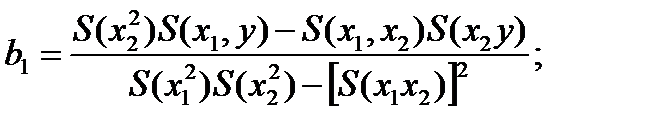(4.94)

(4.95)

(4.96)

где 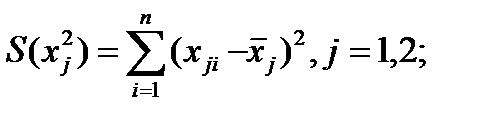(4.97)

(4.98)

(4.99)

(4.100)

Дисперсия, характеризующая разброс значений y_i вокруг линии регрессии, равна:

(4.101)

Проверка значимости коэффициентов в уравнении регрессии (4.93) осуществляется по следующему алгоритму:

(4.102)

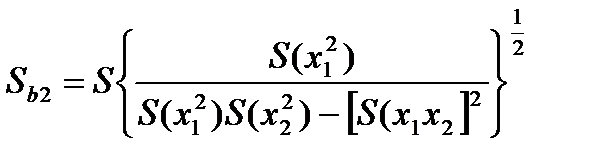(4.103)

Статистика t имеет распределение Стьюдента с f=n-3 степенями свободы.

Если:

, (4.104)

то коэффициенты b₁и b₂ признаются значимыми.

Сама регрессия признается значимой, если:

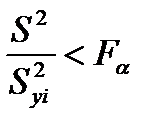, (4.105)

где 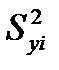- дисперсия значений y_i, оцениваемая по дублируемым наблюдениям.

Для F_α используются степени свободы f₁=n-3 и f₂=m-1, где m – объем выборки, по которой производилась оценка . Табличные значения F_α определяются из соответствующей литературы, например [8].

Для большего числа независимых переменных расчеты и анализ множественной регрессии существенно усложняются. Однако, в настоящее время разработаны специальные методы планирования регрессионных экспериментов, позволяющие упростить расчет коэффициентов регрессии и сократить число необходимых экспериментов.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Холян, А.М. Введение в инженерное исследование / А.М. Холян, М.П. Рудницкий. – Свердловск: УПИ, 1984. – 96 с.

2. Рогов В.А. Методика и практика технических экспериментов: Учеб. пособие для студ. высш. учеб. заведений / В.А. Рогов, Г.Г. Позняк. – М.: Издательский центр «Академия», 2005. – 288 с.

3. Крутов В.И. Основы научных исследований: Учеб. для техн. вузов / В.И. Крутов, И.М. Грушко, В.В. Попов и д.р.; Под ред. В.И. Крутова, В.В. Попова. – М.: Высш. шк., 1989. – 400 с.

4. Спирин Н.А. Методы планирования и обработки результатов инженерного эксперимента: Уч. пос. для вузов / Н.А. Спирин, В.В. Лавров, В.И. Лобанов и др.; Под ред. Н.А. Спирина. – Екатеренбург, 2006. – 306 с.

5. Вентцель Е.С. Овчаров Л.А. Теория вероятностей и ее инженерные приложения. Учеб. пособие для втузов. – 2-е изд., стер. – М.: Высш. шк., 2000. – 480 с.

6. Горяинов В.Б. Математическая статистика: учеб. для втузов / В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова и др.; Под ред. В.С. Зарубина, А.П. Крищенко. – М.: МГТУ им. Н.Э. Баумана, 2001. – 423 с

7. Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. – СПб.: Лань, 1999. – 224 с.

8. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

9. Зажигаев Л.С. Методы планирования и обработки результатов физического эксперимента / Л.С. Зажигаев, А.А. Кишьян, Ю.И. Романиков. – М.: Атомиздат, 1978. – 232 с.

10. Гришин А.С. Математическое моделирование в экологии: Учеб. пособие для вузов / А.С. Гришин, Н.А. Орехов, В.Н. Новиков. – М.: ЮНИТИ-ДАНА, 2003. – 269 с.

11. Ящерицын П.И. Планирование эксперимента в машиностроении: [Справ. пособие] / П.И. Ящерицын, Е.И. Махаринский. – Мн.: Высш. шк., 1985. – 286 с.

12. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006. – 816 с.

13. Пустыльник Е.И. Статистические методы анализа и обработки результатов наблюдений. – М.: Наука, 1968.

14. Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1988. – 239 с.

15. Браверман Э.М. Структурные методы обработки эмпирических данных / Э.М. Браверман, И.Б. Мучник. – М.: Наука, 1983. – 464 с.

Приложения