Оценка адекватности регрессии

Количественной мерой адекватности является отношение дисперсии S², определяемой рассеянием значений y_i вокруг линии регрессии, к дисперсии S_y², определяемой рассеянием значений y_i вокруг своих средних .

Если:

                                    ,                                    (4.79)

где  - α – квантиль распределения Фишера с f₁=n-2 и f₂=m-1 степенями свободы.

 Тогда ошибка в определении регрессии с доверительной вероятностью α признается статистически значимой (m – объем выборки, по которой выполнена оценка дисперсии S_y², т.е. число дублируемых наблюдений для каждой серии y_i).

Если дисперсия S_y² определяется по дублируемым значениям y_i, то оценкой является средневзвешенная дисперсия:

                                                                      (4.80)

                           где                             (4.81)

                                                                             (4.82)

Пример: проверить адекватность регрессии для данных:

xi	1,2	2,4	2,8	4,2	5,9	6,8	8,1	9,2	10,1	11,0
yi	7	12	17	24	29	38	46	45	54	68

 Доверительная вероятность α=0,95.  Для оценки S_y² предварительно проводилась серия наблюдений над случайной величиной у при неизменной величине x (m=10):

yij

12

14

11

10

8

6

7

15

13

Получаем: S²=13,4755. По отдельной серии наблюдений находим оценку:

Далее имеем:

 Из таблиц F–распределения [8] имеем: .

Так как F=1,148 < F_0,95(8,8)=3,438, то с вероятностью α=0,95 следует сделать вывод о статистической неразличимости сравниваемых дисперсий, а следовательно, об адекватности уравнения регрессии.

 

4.3.2.2.2. АНАЛИЗ РЕГРЕССИОННЫХ ОСТАТКОВ [12]

Определенную информацию об адекватности уравнения регрессии дает исследование остатков вида 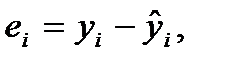. Если выборочная регрессия  удовлетворительно описывает истинную зависимость между у и х, то остатки  должны быть независимыми (см. ниже) нормально распределенными случайными (см. раздел 4) величинами, с нулевым средним и в значениях e_i должен отсутствовать тренд.

Независимость в последовательности значений е_i (i=1,…,n) может быть проверена с помощью сериального коэффициента корреляции Дарбина-Ватсона [41]. Статистика сериального коэффициента корреляции Дарбина-Ватсона имеет вид:

                                                                    (4.83)

где е – разница между наблюдаемым и предсказанным в модели значением зависимой переменной.

Автокорреляция остатков обычно свидетельствует об ошибках в спецификации модели, например, о неправильно выбранной форме связи между переменными, о не включении в модель существенного фактора. Модель с автокорреляцией в остатках нельзя использовать для дальнейшего анализа, так как полученные результаты будут недостоверными.

Выводы о наличии, либо отсутствии автокорреляции делаются на основе специальных статистических таблиц, в которых для заданного числа наблюдений n, уровня a (доверительная вероятность) иk (число независимых переменных) указаны критические значения d₁ и d₂ (таблица 4.16).

 

Положительной автокорреляция.	Зона неопределенности	Отсутствие автокорреляции.	Зона неопределенности	Отрицательной автокорреляция.
0                 d1                   d2                4 - d2               4 – d1                 d Рис. 4.6 Шкала статистики Дарбина - Уотсона     В результате сравнения рассчитанной статистики d с табличными значениями возможны следующие ситуации:

1. d<d₁. Данная ситуация свидетельствует о положительной автокорреляции остатков. Полученную модель использовать нельзя.

2. D₁≤d≤d₂. Рассчитанная статистика попала в зону неопределенности. Нельзя ни подтвердить, ни отвергнуть гипотезу об отсутствии автокорреляции остатков. Дальнейшие выводы по такой модели должны быть очень осторожными.

3. D₂<d<4-d_2. Гипотеза об отсутствии автокорреляции подтверждается. Модель можно использовать для анализа.

4. 4-d₂≤d≤4-d_{1 .} Рассчитанная статистика попала в зону неопределенности. Нельзя ни подтвердить, ни отвергнуть гипотезу об отсутствии автокорреляции остатков. Дальнейшие выводы по такой модели должны быть очень осторожными.

5. d>4-d_1. Данная ситуация свидетельствует об отрицательной автокорреляции остатков. Полученную модель использовать нельзя.

 

Таблица 4.16

Критические значения статистики Дарбина-Ватсона [12]

n	α	k
		1		2		3		4		5
		D1	D2	D1	D2	D1	D2	D1	D2	D1	D2
15   20   25	0,95 0,99 0,95 0,99 0,95 0,99	1,08 0,81 1,20 0,95 1,29 1,05	1,36 1,07 1,41 1,15 1,45 1,21	0,95 0,70 1,10 0,86 1,21 0,98	1,54 1,25 1,54 1,27 1,55 1,30	0,82 0,59 1,00 0,77 1,12 0,90	1,75 1,46 1,68 1,41 1,66 1,41	0,69 0,49 0,90 0,68 1,04 0,83	1,97 1,70 1,83 1,57 1,77 1,52	0,56 0,39 0,79 0,60 0,95 0,75	2,21 1,96 1,99 1,74 1,89 1,65

Окончание таблицы 4.16

 

n	α	k
		1		2		3		4		5
		D1	D2	D1	D2	D1	D2	D1	D2	D1	D2
30   40   50   60   80   100	0,95 0,99 0,95 0,99 0,95 0,99 0,95 0,99 0,95 0,99 0,95 0,99	1,35 1,13 1,44 1,25 1,50 1,32 1,55 1,38 1,61 1,47 1,65 1,52	1,49 1,26 1,54 1,34 1,59 1,40 1,62 1,45 1,66 1,52 1,69 1,56	1,28 1,07 1,39 1,20 1,46 1,28 1,51 1,35 1,59 1,44 1,63 1,50	1,57 1,34 1,60 1,40 163 1,45 1,65 1,48 1,69 1,54 1,72 1,58	1,21 1,01 1,34 1,15 1,42 1,24 1,48 1,32 1,56 1,42 1,61 1,48	1,65 1,42 1,66 1,46 1,67 1,49 1,69 1,52 1,72 1,57 1,74 1,60	1,14 0,94 1,29 1,10 1,38 1,20 1,44 1,28 1,53 1,39 1,59 1,46	1,74 1,51 1,72 1,54 1,73 1,56 1,74 1,60 1,76 1,63 1,76 1,63	1,07 0,88 1,23 1,05 1,34 1,16 1,41 1,25 1,51 1,36 1,57 1,44	1,83 1,61 1,79 1,58 1,77 1,59 1,77 1,60 1,77 1,62 1,78 1,65

 

Пример: для полученных в результате эксперимента данных (n=15) проверить наличие корреляции регрессионных остатков критерием Дарбина-Ватсона при доверительной вероятности α=0,95:

xi	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15;
yi	7	8	6	9	11	10	14	13	18	19	11	14	18	16	16

Вычислим оценки регрессии методом наименьших квадратов:

Тогда:

Находим регрессионные остатки по уравнению:

Получаем следующие значения:

0,3417; 0,1024; 2,8631; 0,6238; -0,6155; 1,1452; -2,0941; -0,3334; -4,5727; -4,8120; 3,848; 1,7094; -1,5299; 1,2308; 1,9915.

Вычисляем статистику Дарбина-Ватсона:

Из таблицы 4.16 для α=0,95, k=1 (так как регрессия y=a+b·x, имеем одну независимую переменную) и n=15 имеем D₁(0,95)=1,08 и D₂(0,95)=1,36.

Строим шкалу статистики Дарбина - Ватсона (см. рисунок 4.6) и попадаем в зону отсутствия автокорреляции остатков. Следовательно, наличие корреляции остатков регрессионной модели y=6,581+0,7606·x с достоверностью α=0,95 отклоняется.