Рассмотренный ранее однофакторный дисперсионный анализ обладает информативностью, не большей, чем методы множественного сравнения. Информативность дисперсионного анализа возрастает при одновременном изучении влияния нескольких факторов.
Рассмотрим случай, когда анализируется влияние одновременно двух факторов А и В на уровнях А1, А2,… Аk, и В1, В2,…, Вm соответственно (таблица 4.7)
Таблица 4.7
Результаты исследования
| В | А |
| |||||
| А1 | А2 | … | Аi | … | Аk | ||
| В1 В2 . . . Вj . . . Вm | x11 x12 … … … x1j … … … x1m | x21 x22 … … … x2j … … … x2m | … … … … … … … … … … | xi1 xi2 … … … xij … … … xim | … … … … … … … … … … | xk1 xk2 … … … xkj … … … xkm | X1’ X2’ … … … Xj’ … … … Xm’ |
| X1 | X2 | … | Xi | … | Xk | |
Дисперсионный анализ для двухфакторных таблиц проводится в следующей последовательности:
- Вычисляются суммы:
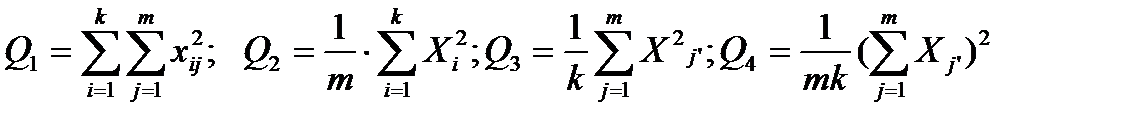(4.29)
- Далее находятся оценки дисперсий:
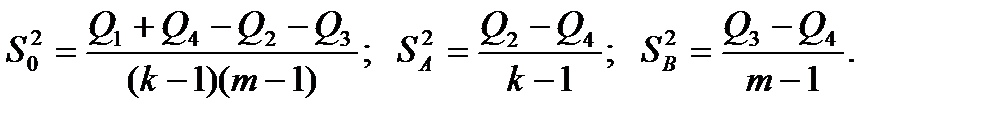(4.30)
Если:
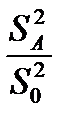> Fα(f1;f2), (4.31)
где f1=k-1 и f2=(k-1)*(m-1), то влияние фактора А с достоверностью α признается значимым.
Аналогично значимым признается влияние факторов В (f1=m-1 и f2=(k-1)*(m-1)).
Приведенный анализ предполагает независимость факторов А и В. Если они зависимы, то взаимодействие факторов С=А*В также является фактором, которому соответствует своя дисперсия. Для того, чтобы выделить такое взаимодействие, необходимы параллельные наблюдения в каждой клетке таблицы, т.е. при каждом сочетании факторов А и В на уровнях Ai и Bi соответственно необходимо не одно наблюдение, а серия наблюдений xij1, xij2,…, xijn. Пусть xij теперь является средним из n наблюдений, т.е.:
. (4.32)
Для оценки влияния взаимодействия факторов А*В вычисляем дополнительную сумму:
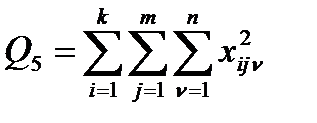. (4.33)
Далее анализ производится, как и ранее, с той лишь разницей, что в клетках таблицы вместо отдельных значений 
, используются их средние значения (4.32) 
.
- Вычисляется дисперсия:
(4.34)
- Проверяется значимость взаимодействия факторов А*В критерием:
, (4.35)
где f1=(k-1)*(m-1) и f2=m*k*(n-1).
С добавлением каждого нового фактора принципиальная основа дисперсионного анализа не изменяется, но существенно усложняются формулы и таблицы для расчетов. Подробное изложение прикладных методов дисперсионного анализа для случая трех, четырех и более факторов с анализом различных практических ситуаций содержится в [13].
Пример [12]: Провести двухфакторный дисперсионный анализ данных, представленных в таблице 4.8, при доверительной вероятности α=0,95.
Таблица 4.8
Результаты исследования
| В | А | ||
| А1 | А2 | А3 | |
| В1 В2 В3 В4 | 3,6 3,8 4,1 4,2 4,0 4,1 3,8 3,5 3,6 3,4 3,2 3,2 | 2,9 3,1 3,0 3,3 2,9 3,2 3,6 3,7 3,5 3,4 3,6 3,5 | 2,6 2,5 2,9 3,7 3,5 3,6 3,2 3,0 3,4 3,6 3,8 3,7 |
Заменяя серии значений их средними, получаем следующую таблицу 4.9.
Таблица 4.9
