В качестве факторов можно выбирать только контролируемые и управляемые переменные, т.е. такие, которые исследователь может поддерживать постоянными в течение каждого опыта на заданном уровне. В число факторов должны быть включены параметры процесса, оказывающие наиболее сильное влияние на функцию отклика. Необходимо заметить, что, несмотря на всю заманчивость и очевидное преимущество активного спланированного эксперимента перед пассивным, в его применении имеется целый ряд трудностей, связанных с определенными ограничениями на его реализацию. Важнейшим условием применимости этого подхода является управляемость процессов по каждому из выбранных факторов, т.е. возможность независимого изменения каждого из этих факторов и поддержания его на заданном уровне в период проведения опытов.
Для каждого фактора необходимо указать интервал изменения параметров, в пределах которого ставится исследование. Для этого на основе априорной информации устанавливаются ориентировочные значения факторов х10, х20,…, хi0,…, хk0. Этой комбинации значений факторов соответствует точка в многомерном факторном пространстве, которая принимается за исходную точку. Координаты этой точки принимаются за основной (нулевой) уровень.
Интервалом варьирования факторов называется некоторое число (каждое для соответствующего фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний пределы [2, 11]. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так чтобы верхний уровень составлял +1, нижний -1, а основной – 0.
Для факторов с непрерывной областью определения это достигается с помощью преобразования (кодирования) факторов.
В теории планирования экспериментов показано, что минимально необходимое число уровней факторов на единицу больше порядка уравнения.
Для простоты изложения примем, что y=f(x1,x2).
Пусть каждому фактору соответствует координатная ось (это можно сделать, так как факторы независимы). Образованное таким образом пространство называется факторным (рис.3.1) [2, 11].
Рис. 3.1 Переход от реальных факторов к кодированным
Отметим диапазоны изменения факторов: xi min – нижний уровень; xi max – верхний уровень; i=1,2. Найдем середины этих диапазонов - основные уровни [2, 11]:
(3.7)
и шаг варьирования фактора:
(3.8)
Перенесем начало координат в точку 0 (х10,х20) и перейдем к новым координатам по формуле:
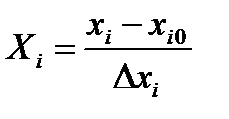. (3.9)
Назовем Xi – кодированными координатами. В кодированном виде верхний уровень любого фактора имеет значение «+1», нижний – «-1», основной – «0». Кодирование уровней факторов проводится для удобства записи условий эксперимента и обработки экспериментальных данных.
3.2.2. МЕТОД ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА [2, 9, 10]
Рассмотрим случай, когда функция отклика линейно зависит от трех независимых факторов. План эксперимента представлен в табл. 3.1.
Таблица 3.1
План эксперимента для трех факторов
| Номер опыта | план | Результат yi | |||||||
| X0 | X1 | X2 | X3 | X1*X2 | X1*X3 | X2 *X3 | X1* X2 *X3 | ||
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | y1 |
| 2 | +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | y2 |
| 3 | +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | y3 |
| 4 | +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | y4 |
| 5 | +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | y5 |
| 6 | +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | y6 |
| 7 | +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | y7 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | y8 |
Здесь добавлен столбец фиктивной переменной X0, нужный для оценки свободного члена b0. После реализации получают 8 уравнений с 8 неизвестными, их решение и даст оценку всех восьми коэффициентов регрессии b0,b1,…, b3,b12,…, b123.
План, в котором число опытов равно числу определяемых коэффициентов, называется насыщенным.
В данном плане были использованы все точки с «крайними» координатами, т.е. 
(все возможные комбинации выбранных уровней: 2k=8 (k – число факторов)). Если эксперименты проводятся только на двух уровнях (при двух значениях факторов) и при этом в процессе эксперимента осуществляются все возможные неповторяющиеся комбинации из k факторов, то постановка опытов по такому плану носит название полного факторного эксперимента (ПФЭ) или 2k
Таким образом, полный факторный эксперимент (ПФЭ) – это эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов.
Кодированный план геометрически может быть интерпретирован в виде куба, восемь вершин которого представляют собой восемь экспериментальных данных (рис. 3.2).
При числе факторов k=2 построение матрицы ПФЭ не вызывает затруднений, при увеличении же числа факторов возникает необходимость в некоторых специальных приемах построения матрицы.
Например, прием основанный на чередовании знаков: в первом столбце (для X1) знаки чередуются поочередно. Во втором (для X2) – через 2 знака, в третьем (для X3) – через 4 знака и т.д. по степеням 2k.
Рис. 3.2. Геометрическое изображение ПФЭ
Матрица ПФЭ обладает следующими свойствами:
- Свойство симметричности: алгебраическая сумма элементов вектор – столбца каждого фактора равна нулю (за исключением столбца, соответствующего свободному члену):
, (3.10)
где i- номер фактора; j–номер опыта.
- Свойство нормирования: сумма квадратов элементов каждого столбца равна числу опытов:
; (3.11)
- Свойство ортогональности: скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых двух вектор-столбцов матрицы) равно нулю:
(3.12)
Планы, для которых выполняется свойство 3, называется ортогональными. Благодаря этому свойство резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии.
Поскольку результаты наблюдений отклика носят случайный характер, приходится в каждой точке плана проводить не один, а m* параллельных опытов (обычно m*=2 
4).
В каждой серии экспериментов их последовательность рандомизируется, т.е. с помощью таблиц случайных чисел определяется случайная последовательность реализации экспериментов. Рандомизация дает возможность свести эффект некоторого случайного фактора к случайной погрешности. Это позволяет в определенной степени исключить предвзятость и субъективизм исследователя. Пусть, например, требуется рандомизировать 8 опытов, обозначенных цифрами I,II,…,VIII. Поставим им в соответствие любые 8 последовательных чисел, взятых в любой строке или в любом столбце таблицы случайных чисел. Если при этом встретятся повторяющиеся числа, то их следует отбросить. Например, могут быть получены следующие пары: I – 60; II – 12; III – 05; IV – 15; V – 34; VI – 30, VII – 18, VIII - 70.Расположив случайные числа в порядке возрастания (или убывания), получим искомую последовательность реализации опытов: III, II, IV, VII, VI, V, I, VIII (или VIII, I, V, VI, VII, IV, II, III).
