Дисперсионный анализ является статистическим методом анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, с целью выбора наиболее значимых факторов и оценки их влияния на исследуемый процесс.
Влияние различных факторов на изучаемые случайные величины (например, влияние режима нагрузки на долговечность технического изделия) приводит к изменению значений параметров распределения вероятностей этих величин – среднего, дисперсии или моментов более высокого порядка.
С помощью дисперсионного анализа устанавливаются изменения дисперсии результатов эксперимента при изменении уровней изучаемого фактора. Если дисперсии будут отличаться значимо, то следует вывод о значимом влиянии фактора на среднее значение наблюдаемой случайной величины.
Классические методы дисперсионного анализа основываются на следующих предпосылках: распределение исходных случайных величин нормально; дисперсии экспериментальных данных одинаковы для всех условий эксперимента (т.е. для экспериментов, выполненных на различных уровнях изучаемого фактора).
Поэтому, при проведении дисперсионного анализа следует предварительно проверить нормальность распределения изучаемой случайной величины и неразличимость дисперсий изучаемых совокупностей.
ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ПРИ ПОМОЩИ МОДИФИЦИРОВАННОГО КРИТЕРИЯ Χ2 [9, 12]
С помощью данного критерия оцениваются параметры распределения по негруппированной выборке. После оценки параметров распределения совокупность выборочных данных разбивается на k равновероятных интервалов ( ) и статистика критерия подсчитывается по формуле:
) и статистика критерия подсчитывается по формуле:
 (4.1)
(4.1)
где n – объем выборки; mi – количество членов выборки, попавшее в i-й интервал.
Границы интервалов определяются следующим образом:
 (4.2)
(4.2)
где 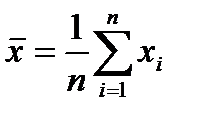 (4.3)
(4.3)
и  . (4.4)
. (4.4)
Значение коэффициентов ci приведены в таблице 4.1 [4]. Следует помнить, что с0=-∞ и сk=∞.
Таблица 4.1
Значения коэффициентов ci модифицированного χ2- критерия нормальности для k =3  15
15
| k | c1 | c2 | c3 | c4 | c5 | c6 | c7 |
| 3 4 5 6 7 8 9 10 11 12 13 14 15 | -0,4307 -0,6745 -0,8416 -0,9674 -1,0676 -1,1503 -1,2206 -1,2816 -1,3352 -1,3830 -1,4261 -1,4652 -1,5011 | 0 -0,2533 -0,4307 -0,5659 -0,6745 -0,7647 -0,8416 -0,9085 -0,9674 -1,0201 -1,0676 -1,1108 | 0 -0,1800 -0,3186 -0,4307 -0,5244 -0,6046 -0,6745 -0,7363 -0,7916 -0,8416 | 0 -0,1397 -0,2533 -0,3488 -0,4307 -0,5024 -0,5660 -0,6229 | 0 -0,1142 -0,2194 -0,2934 -0,3661 -0,4307 | 0 -0,0966 -0,1800 -0,2533 | 0 -0,0837 |
Так как ci симметричны относительно нуля, то недостающие знаки ci можно найти из соотношений:
 для нечетных
для нечетных  ; (4.5)
; (4.5)
 для четных
для четных  . (4.6)
. (4.6)
Если χ2 > dk(α), где dk(α) – критическое значение статистики критерия на уровне значимости α, то гипотеза нормальности отклоняется. Критические значения dk(α) приведены в таблице 4.2 [12].
Таблица4.2






