| Границы интервалов | 
| 
|
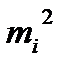
| 1 2 3 4 5 6 7 8 9 10 | -∞  72,79
72,79 82,40
82,40 89,32
89,32 95,24
95,24 100,77
100,77 106,30
106,30 112,22
112,22 119,14
119,14 128,40
128,40 ∞
| 7 12 11 11 8 13 6 12 10 10 | 49 144 121 121 64 169 36 144 100 100 |
|
| 100 | 1048 | |
Статистика критерия равна:
χ2= 
Из таблицы 4.2 находим критическое значение статистики для k=10 и α=0,1: d10(0,1)=12,384. Так как χ2=4,8<d10(0,1)=12,384, гипотеза нормальности исходного распределения вероятностей не отклоняется.
ПРОВЕРКА ГИПОТЕЗЫ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ ПРИ ПОМОЩИ КРИТЕРИЯ ФИШЕРА [9, 12]
Если выборочными оценками максимального правдоподобия дисперсий являются:
и 
, (4.7)
то статистика критерия Фишера записывается как:
F= 
(4.8)
В числителе всегда должна стоять большая по величине из двух сравниваемых дисперсий. При справедливости гипотезы: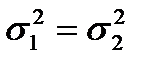 
статистика критерия имеет распределения Фишера с 
и 
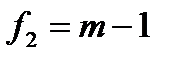степенями свободы, где n и m–объемы сравниваемых выборок.
Если:
F >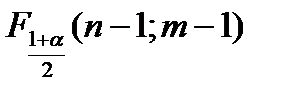 
и F > 
, (4.9)
то гипотеза отклоняется в пользу альтернативы: 
.
Если:
F > 
, (4.10)
то нулевая гипотеза отклоняется в пользу альтернативы: 
(α-доверительная вероятность).
Критерий Фишера очень чувствителен к отклонениям от нормальности распределения 
. Его устойчивость к отклонениям от нормальности может быть повышена соответствующей корректировкой степеней свободы. Вместо f1 и f2 в этом случае используются степени свободы 
и 
, где
, (4.11)
. (4.12)
В дальнейшем процедура проверки гипотезы не отличается от обычного F–критерия. Критические значения F – статистики приведены в соответствующих таблицах [12].
Пример: Имеются две выборки нормально распределенных случайных величин (n=m=10):
xi: 2,1; 3,1; 4,8; 6,1; 7,4; 8,5; 10,1; 12,1; 14,0; 15,6;
yi: 4,6; 6,1; 8,2; 9,8; 9,9; 10,4 13,1; 14,5; 16,1; 19,1.
Необходимо проверить гипотезу равенства дисперсий: 
против альтернативы: 
при доверительной вероятности α=0,95.
Имеем:
Так как F =1,016 < F0,975 (9;9)=4,03, нулевая гипотеза не отклоняется.
Рассмотрим теперь критерий со скорректированными степенями свободы. Имеем
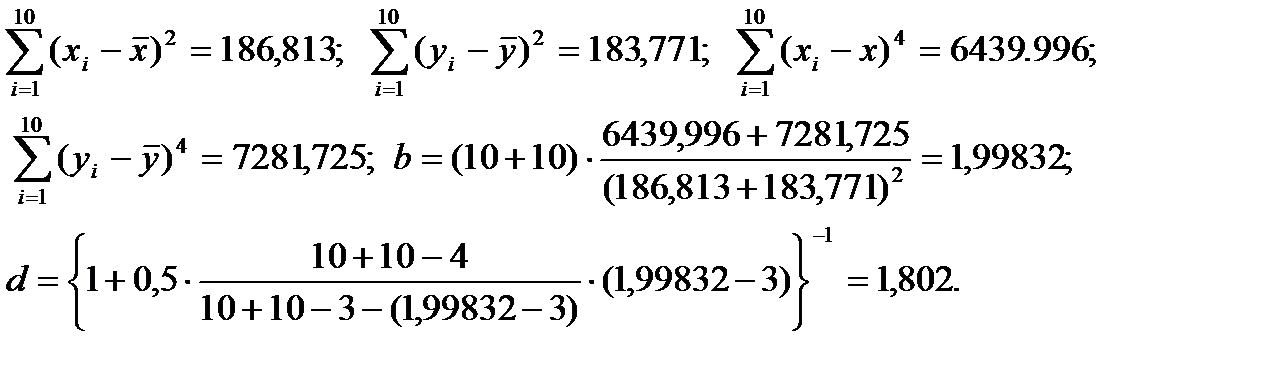
Окончательно имеем 
и 
Из таблиц [8, 12] для дробных степеней свободы и 
имеем 
Так как F=1,016 < 
нулевая гипотеза не отклоняется и в этом случае.
ПРОВЕРКА ГИПОТЕЗЫ РАВЕНСТВА НЕСКОЛЬКИХ ДИСПЕРСИЙ (K > 2) ПРИ ПОМОЩИ КРИТЕРИЯ Кохрана [9, 12]
В литературе [9, 12] рассмотрены различные критерии сравнения нескольких дисперсий, остановимся подробно на критерии Кохрана для случая выборок равных объемов (ni = n при i=1,2,…,k):
. (4.13)
Если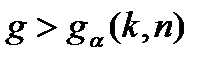 
, то нулевая гипотеза отклоняется. Значения приведены в таблице 4.4 [12]. Критические отношения можно найти также, используясь таблицами F – распределения.
Приме: имеются четыре выборки (к = 4) объема n = 5 каждая:
Хi1: 3, 4, 5, 6, 7; Xi2: 2, 8, 9, 11, 15;
Xi3: 9, 11, 15, 20, 28; Xi4: 4, 6, 8, 10, 16.
Проверить гипотезу равенства дисперсий критерием Кохрана при доверительной вероятности α=0,95.
Имеем: 
Тогда: 
Из таблицы 4.4 для n=5, k=4 и α=0,95 имеем 
Так как g=0,558<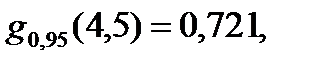 
нулевая гипотеза не отклоняется.
Таблица 4.4
Критические значения 
статистики Кохрана для доверительной вероятности α=0,95
| k | n | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 17 | 37 | |
| 2 3 4 5 6 7 8 9 10 15 20 30 | 0,999 0,993 0,967 0,928 0,883 0,838 0,794 0,754 0,707 0,548 0,480 0,363 | 0,995 0,942 0,864 0,788 0,722 0,664 0,615 0,573 0,536 0,407 0,330 0,241 | 0,979 0,883 0,781 0,696 0,626 0,568 0,521 0,481 0,447 0,332 0,265 0,191 | 0,959 0,833 0,721 0,633 0,563 0,508 0,463 0,425 0,393 0,288 0,229 0,163 | 0,937 0,793 0,676 0,587 0,519 0,466 0,423 0,387 0,357 0,259 0,205 0,145 | 0,917 0,761 0,641 0,553 0,487 0,435 0,393 0,359 0,331 0,239 0,188 0,133 | 0,899 0,733 0,613 0,526 0,461 0,410 0,370 0,338 0,311 0,223 0,175 0,123 | 0,822 0,711 0,590 0,504 0,440 0,391 0,352 0,321 0,294 0,210 0,165 0,116 | 0,867 0,691 0,570 0,485 0,423 0,375 0,337 0,307 0,281 0,200 0,157 0,110 | 0,854 0,673 0,554 0,470 0,408 0,362 0,325 0,295 0,270 0,192 0,150 0,105 | 0,795 0,606 0,488 0,409 0,353 0,310 0,278 0,251 0,230 0,161 0,125 0,087 | 0,707 0,515 0,406 0,335 0,286 0,249 0,221 0,199 0,181 0,125 0,096 0,066 |
4.1.1. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ [12, 13]
Предположим что анализируется влияние фактора А, изучаемого на k уровнях (А1,А2,…,Аk). На каждом уровне Ai проведены n наблюдений (xi1, xi2,… xin). Следовательно, на всех k уровнях фактора А произведены k*n наблюдений.
Рассмотрим последовательность проведения дисперсионного анализа. Расположим экспериментальные данные в виде таблицы:
Таблица 4.5
Экспериментальные данные
| Номер наблюдения | Уровни фактора А |
| А1 А2 … Аi … Аk | |
| 1 2 . j . n | x11 x21 … xi1 … xk1 x12 x22 … xi2 … xk2 ... .… ... … …. … x1j x2j… … x i j … x k j . . … ... … … … x1n x2n … … xi n …. x k n |
| X1 X2 … Xi … Xk |
Рассмотрим оценки различных дисперсий, возникающие при анализе таблицы результатов наблюдений. Для дисперсии, характеризующей изменение данных на уровне Ai (по строкам таблицы), имеем:
. (4.14)
Из предпосылок дисперсионного анализа следует, что должно иметь место равенство 
, что проверяется соответствующим критерием сравнения.
При выполнении условия 
(при i=1,2,…k) находим оценку дисперсии, характеризующей рассеяние значений xij вне влияния фактора А, по формуле:
. (4.15)
Оценка 
имеет k*(n-1) степеней свободы.
Общая выборочная дисперсия всех наблюдений равна:
(4.16)
(4.17)
(4.18)
Следовательно:
. (4.19)
Введем теперь оценку дисперсии 
, характеризующей изменение средних 
, связанное с влиянием фактора А:
(4.20)
Очевидно, что при оценке 
используется (k-1) степеней свободы. Теперь проверка влияния фактора А на изменение средних может быть сведена к сравнению дисперсий и . Влияние фактора А признается значимым, если значимо отношение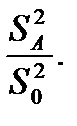 
Отношение 
признается значимым с вероятностью α, если:
, (4.21)
где 
- α- квантиль F- распределения с 
степенями свободы.
Для нахождения могут быть использованы специальные таблицы, например, из [2].
Для упрощения вычислений приведем алгоритм их выполнения [12]:
- Вычисляем последовательно суммы:
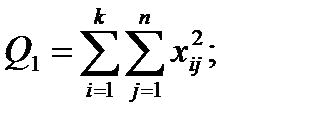(4.22)
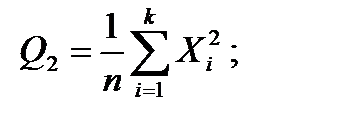(4.23)
(4.24)
- Далее находим:
(4.25)
(4.26)
Сравнением и , устанавливаем наличие влияние фактора А.
Если:
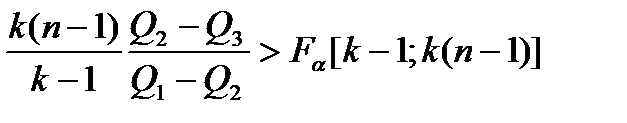, (4.27)
то влияние фактора А признается значимым. В ином случае всю выборку наблюдений можно считать однородной с общей дисперсией:
. (4.28)
Пример: Провести дисперсионный анализ данных, представленных в таблице 4.6, при доверительной вероятности α=0,95.
Таблица 4.6
Результаты исследования
| j | Уровни фактора Аi | ||||
| A1 | A2 | A3 | A4 | A5 | |
| 1 2 3 4 5 6 | 3,2 3,1 3,1 2,8 3,3 3,0 | 2,6 3,1 2,7 2,9 2,7 2,8 | 2,9 2,6 3,0 3,0 3,0 2,8 | 3,6 3,4 3,2 3,3 3,5 3,3 | 3,0 3,4 3,0 3,5 2,9 3,1 |
| 18,5 | 16,8 | 17,4 | 20,3 | 19,1 |
Вычисляем:
Далее вычисляем дисперсии:
Из таблиц для f1=k-1=4 и f2=k(n-1)=25 находим F0,95(4;25)=2,8. Так как 
>F0,95(4;25)=2,8, влияние фактора А на поведение наблюдаемых случайных величин следует признать значимым.
