| месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Число остановок (Xi) | 1 | 2 | 3 | 2 | 1 | 2 | 3 | 1 | 2 | 2 |
В данном примере число остановок компрессорной установки в течение года – это дискретная случайная величина. В первом из n = 10 измеренной этой величины было получено значение x 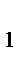 =1, во втором - x
=1, во втором - x 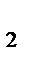 = 2 и т.д., до x
= 2 и т.д., до x 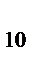 =2.
=2.
Каждому значению дискретной величины Х (любому из событий А, когда случайная величина Х принимает какое – либо строго определенное значение х), можно поставить в соответствии следующее отношение:
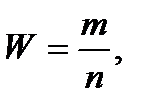 (2.2)
(2.2)
где m – число наблюдений, в которых дискретная величина Х оказалась равна х; n – общее количество наблюдений. Величину W называют частой реализации события А.
В примере 2.1 в пяти наблюдениях: X = 2; 4; 6; 9; 10 количество остановок в течении года x оказалось равным четырем (x=2), следовательно, частота реализации такого события, как две остановки, равна 5/10 = 0,5.
Если продолжить наблюдение за работой компрессорной установки в течение еще двух лет, то, конечно же, совершенно не обязательно, что на протяжении следующих двух лет частота реализации этого события окажется равной 0,5. Однако при возрастании числа повторений одного и того же комплекса условий частота реализации такого события, как, например, две остановки компрессорной установки в течение года, будет принимать все более и более устойчивое значение. Предел, к которому стремится отношение m/n при неограниченном возрастании числа опытов n, называется вероятностью случайного события.
5. Вероятность P (A) события А – число от нуля до единицы, которое представляет собой предел частоты реализации события А при неограниченном числе одного и того же комплекса опытов.
Для дискретной случайной величины можно указать вероятность с которой она принимает каждое из своих возможных значений конечного или счетного множества действительных чисел. Для непрерывной случайной величины задают вероятность ее попадания в один из заданных интервалов области ее определения (поскольку вероятность того, что она примет какое – либо конкретное значение, стремится к нулю).
Полностью свойства случайной величины описываются законом ее распределения, под которым понимают связь между возможными значениями случайной величины и соответствующими им вероятностями.
6. Распределение случайной величины – функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
В математике используют два способа описания распределений случайных величин: интегральный (функция распределения) и дифференциальный (плотность распределения).
7. Функция распределения F (x) – функция, определяющая для всех действительных х вероятность того, что случайная величина Х принимает значение не больше, чем х.
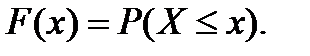 (2.3)
(2.3)
Функция распределения F (x) имеет следующие свойства (рис. 2.1) [5, 6, 7]:
1. Ее ордината, соответствующая произвольной точке x 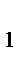 , представляет собой вероятность того, что случайная величина Х будет меньше, чем x
, представляет собой вероятность того, что случайная величина Х будет меньше, чем x 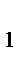 , т.е
, т.е
F(x 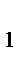 )=
)= 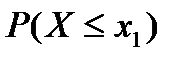 (2.4)
(2.4)
2. Функция распределения принимает значение, заключенное между нулем и единицей:
 (2.5)
(2.5)
3. Функция распределения стремится к нулю при неограниченном уменьшении х и стремится к единице при неограниченном возрастании х, т.е.:


 (2.6)
(2.6)
4. Функция распределения представляет собой монотонно возрастающую кривую, т.е.:
F(x 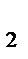 )>F(x
)>F(x 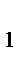 ), (2.7)
), (2.7)
если x 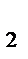 >x
>x 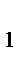 .
.
5. Ее приращение на произвольном отрезке (x 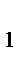 ; x
; x 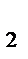 ) равно вероятности того, что случайная величина Х попадает в данный интервал:
) равно вероятности того, что случайная величина Х попадает в данный интервал:
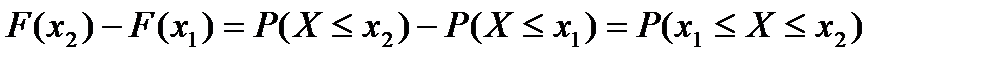 (2.8)
(2.8)

а б
Рис. 2.1 Функции распределения случайной величины: а – дискретной; б – непрерывной
Рассмотрим, какие особенности имеют функции распределения дискретных случайных величин. Пусть Х – дискретная величина, принимающая возможные значения x 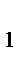 , x
, x 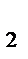 ,…, x
,…, x 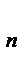 с вероятностями p
с вероятностями p 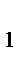 , p
, p 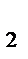 ,…,p
,…,p 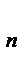 . Функция распределения вероятностей этой случайной величины Х равна:
. Функция распределения вероятностей этой случайной величины Х равна:
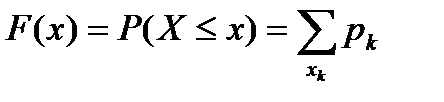 , (2.9)
, (2.9)
где производится суммирование вероятностей всех возможных значений случайной величины Х, меньше чем х.
Такая функция всегда разрывная, ступенчатая (рис. 2.1 а): от - ∞ до x 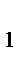 включительно функция равна нулю, в точке x
включительно функция равна нулю, в точке x 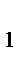 происходит скачок на величину p
происходит скачок на величину p 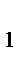 , и функция остается постоянной до x
, и функция остается постоянной до x 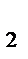 включительно и т.д., то есть возможным значением случайной величины соответствуют скачки функции, равные вероятностям этих значений. Последний скачок на p
включительно и т.д., то есть возможным значением случайной величины соответствуют скачки функции, равные вероятностям этих значений. Последний скачок на p 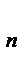 происходит в точке x
происходит в точке x 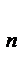 , и функция равна единице от x
, и функция равна единице от x 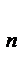 до +∞. Таким образом, сумма всех скачков равна единице.
до +∞. Таким образом, сумма всех скачков равна единице.
8. Плотность распределения f (x) – первая производная (если она существует) функции распределения.
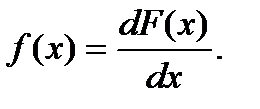 (2.10)
(2.10)
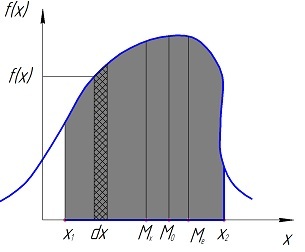
Рис. 2.2 Плотность распределения вероятностей f(x)
Плотность функции распределения f(x) имеет следующие свойства (рис. 2.2):
1. Плотность распределения вероятностей является неотрицательной функцией, т.е. f(x)≥0. Это свойство справедливо, так как F(x) есть неубывающая функция.
2. Функция распределения случайной величины Х равна определенному интегралу от плотности распределения вероятностей в пределах (-∞; х):
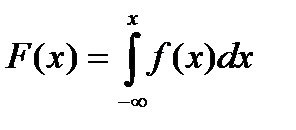 (2.11)
(2.11)
3. Вероятность события, состоящего в том, что случайная величина Х примет значение, заключенное в полуинтервале [x 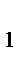 , x
, x 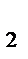 ], равна определенному интегралу от плотности распределения вероятностей на этом полуинтервале:
], равна определенному интегралу от плотности распределения вероятностей на этом полуинтервале:
 (2.12)
(2.12)
4. Интеграл плотности распределения в бесконечно большом интервале (-∞; +∞) равен единице (достоверное событие):
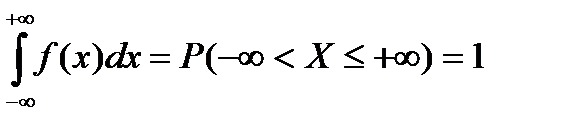 (2.13)
(2.13)
В большинстве случаев при обработке экспериментальных данных, основываясь на тех или иных предложениях (гипотезах) относительно свойств исследуемой величины, удается записать функцию ее распределения, а, следовательно, и плотность распределения как первую производную от функции распределения с точностью до некоторых неизвестных параметров.
Например, для случайной величины, которая удовлетворяет так называемому нормальному закону распределения, функцию распределения можно записать в виде:
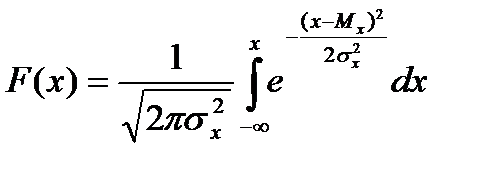 (2.14)
(2.14)
В данной функции константы Mx и σx2 являются параметрами распределений, причем выражение относится к двухпараметрическому виду закона распределения.
9. Параметр распределения – постоянная, от которой зависит функция распределения.
Следовательно, если известен вид функции распределения (каким-либо образом установлено, что случайная величина не противоречит тому или иному закону распределения), то для того, чтобы однозначно охарактеризовать случайную величину, достаточно задать, только лишь параметры ее распределения. Важнейшими параметрами распределения, задающими случайную величину Х, являются ее математическое ожидание Mx (характеризует центр рассеивания) и дисперсия σх2 (характеризует степень рассеивания).
10. Математическое ожидание Mx – среднее взвешенное по вероятностям значение случайной величины.
Для дискретной случайной величины математическое ожидание определяется выражением:
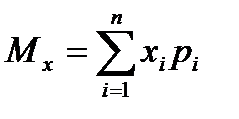 , (2.15)
, (2.15)
где xi – значения дискретной случайной величины, а рi=P(X=xi).
Для непрерывной случайной величины математическое ожидание определяется интегралом:
 , (2.16)
, (2.16)
где f(x) – плотность распределения непрерывной случайной величины.
Можно отметить, что геометрический смысл математического ожидания непрерывной случайной величины – это абсцисса центра тяжести фигуры под кривой плотности распределения f(x). Сказанное проиллюстрируем на рис. 2.2, где видно, что произведение f(x)dx есть площадь элементарного участка под кривой f(x), а х – абсцисса этого участка, т.е. расстояние от начала координат. Следовательно, интеграл дает абсциссу центра тяжести всей площади фигуры под кривой f(x). Кроме математического ожидания центр рассеивания случайной величины можно охарактеризовать такими параметрами ее распределения, как мода и медиана.
11. Мода Мо – значение случайной величины, соответствующее локальному максимуму плотности вероятностей для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
12. Медиана Ме – значение случайной величины, для которого функция распределения принимает значение ½, или имеет место «скачок» со значения, меньшего, чем ½ до значения, большего чем ½.
Таким образом, для дифференциального закона распределения медиана есть такое значение непрерывной случайной величины Х, которое делит пополам площадь под кривой плотности распределения f(x).
13. Дисперсия случайной величины σх2 – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.:
D[X]=M[(Х-Мх)2] (2.17)
Для дискретной случайной величины дисперсия определяется следующим математическим выражением:
 (2.18)
(2.18)
Для непрерывной случайной величины дисперсия определяется выражением:
 , (2.19)
, (2.19)
где х – значение непрерывной случайной величины Х; f(x) – плотность распределения; Мх- математическое ожидание.
Дисперсия имеет размерность квадрата единицы измерения случайной величины, а положительное значение квадратного корня из дисперсии называется средним квадратичным отклонением.
14. Среднее квадратичное отклонение σх - неотрицательный квадратичный корень из дисперсии.
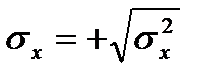 (2.20)
(2.20)
15. Квантиль порядка Р,хр – значение случайной величины, для которого функция распределения принимает значение Р или имеет место “скачок” со значения, меньшего чем Р, до значения большего чем Р:
F(xp)=P (2.21)
Из этого определения квантиля следует, что медиана Ме – это квантиль порядка ½, т.е.:
Ме=X0,5 (2.22)
Вероятность попадания случайной величины Х в интервал [Xp1,Xp2] равна:
Р(Xр1<X≤Xp2)=P(X≤Xp2)-P(X≤Xp1)=F(Xp2)-F (Xp1)=P2-P1 (2.23)
2.2. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ОСНОВНЫЕ ПАРАМЕТРЫ [5, 6, 7]
Функция распределения F(x) и соответствующая ей плотность распределения f(x) представляет собой некоторую математическую модель свойств исследуемой случайной величины (отклика), значения которой регистрируется в ходу эксперимента. Поэтому одной из основных задач статистической обработки опытных данных является нахождение таких функций распределения, которые, с одной стороны, достаточно хорошо описывали бы наблюдаемые значения случайной величины, а с другой – были бы удобны для дальнейшего статистического анализа. При этом вид функции распределения предпочтительно выбирать на основе представлений о физической природе рассматриваемого явления, т.к. в этом случае исключаются возможные погрешности при распространении найденных закономерностей за пределы изучаемого в эксперименте интервала варьирования (изменения) случайной величины (отклика).
Из всех изученных к настоящему времени случайных величин при обработке экспериментальных данных исследователи чаще всего оперируют со случайными величинами, которые имеют так называемое нормальное (Гауссово) распределение (рис. 2.3). Cогласно центральной предельной теореме математической статистики “при определенных условиях распределение нормированной суммы n независимых случайных величин, распределенных по произвольному закону, стремится к нормальному, когда n стремится к бесконечности”. Необходимые условия, при которых эта теорема оказывается справедливой, состоят в том, что различные случайные величины должны иметь конечные дисперсии и дисперсия любой случайной величины не должна быть слишком большой по сравнению с дисперсиями других.
При обработке экспериментальных данных эта теорема имеет очень большое значение, поскольку отклик становится случайной величиной в результате влияния неконтролируемых факторов, число которых, скорее всего, стремится к бесконечности. Кроме того, если при проведении опытов все наиболее существенные факторы контролируются, то воздействие на отклик каждого из неконтролируемых факторов не должно быть слишком большим по сравнению с остальными неконтролируемыми факторами. Другими словами, та дисперсия (рассеивание) отклика, которую вызывает какой – либо из неконтролируемых факторов, не должна сильно отличаться от дисперсий, связанных с влиянием остальных неконтролируемых факторов. В противном случае фактор, дисперсия которого существенно отличается от других, обязательно должен быть переведен в разряд контролируемых.
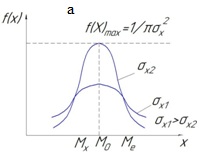
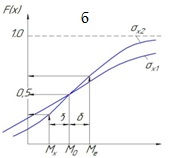

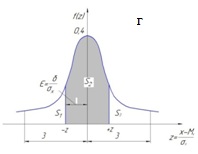
Рис. 2.3. Плотность распределения (а,г) и функция распределения (б,в) при нормальном законе распределения случайных величин
Следовательно, если при планировании эксперимента учтены все наиболее существенные факторы и затем, при проведении опытов, они контролируются, то при обработке экспериментальных данных можно предполагать, что отклик не должен противоречить нормальному распределению. Как правило, нормальному закону подчиняются результаты испытаний стали на прочность, производительность многих металлургических агрегатов, составы сырья, топлива, сплавов, массы слитков, отлитых в однотипные изложницы, случайные ошибки измерения и т.п., поэтому при обработке результатов наблюдений исследователи, прежде всего, предполагают именно нормальное распределение отклика.
Большинство других распределений, которые используются в математической статистики (Стьюдента, Фишера, Пирсона, Кохрена и т.д.), получены на основе нормально распределения. Нельзя, однако, абсолютизировать значение нормального распределения. Не все случайные величины распределены по нормальному закону. Тем не менее, на практике, если явление подвержено действию многих случайных факторов, их суммарное воздействие вполне оправдано можно описать с помощью нормального закона. Как уже было отмечено, для случайной величины, которая не противоречит нормальному закону, функция распределения и соответствующая ей плотность распределения:
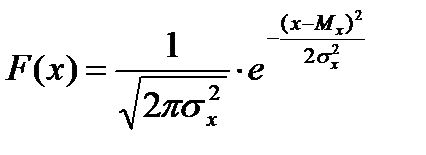 (2.24)
(2.24)
Отметим некоторые свойства нормального закона распределения:
1. Кривая плотности распределения симметрична относительно значения Мx, называемого иногда центром распределения.
2. При больших значениях σх2 кривая f(x) более пологая, т.е σх2 являются мерой величины рассеивания значения случайной величины около значений Мх. При уменьшении параметра σх2 кривая нормального распределения сжимается вдоль оси ОХ и вытягивается вдоль f(x).
3. Максимум ординаты кривой плотности распределения определяются выражением:
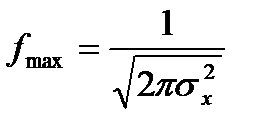 , (2.25)
, (2.25)
что при σх2=1 соответствует значению примерно 0,4.
4. Для нормального распределения математическое ожидание, мода и медиана совпадают:
Мх=М0=Ме (2.25)
В ряде случаев рассматривается не сама случайная величина Х, а ее отклонение от математического ожидания:
Y=X-M (2.26)
Такая случайная величина Y называется центрированной.
Отношение случайной величины Х к ее среднему квадратичному отклонению называется нормированной случайной величиной:
 (2.27)
(2.27)
Таким образом, центрированная случайная величина – разность между данной случайной величиной и ее математическим ожиданием, а нормированная случайная величина – отношение данной случайной величины к ее среднему квадратному отклонению.
Очевидно, что математическое ожидание центрированной случайной величины равно нулю, Му=0, а дисперсия нормированной случайной величины равна единице, σv2=1.
Приведенная случайная величина – центрированная и нормированная случайная величина:
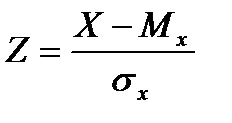 (2.28)
(2.28)
Математическое ожидание и дисперсия приведенной случайной величины Z равна соответственно нулю, Мz=0, и единице, σz2=1.
Нормальное распределение с параметрами Мz=0 и σz2=1 называется стандартным (нормированным).
Для приведенной случайной величины нормальное стандартное распределение принимает вид:
 , (2.29)
, (2.29)
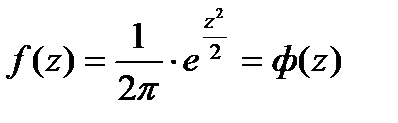 (2.30)
(2.30)
Графики этих функций показаны на рис. 2.3 (в, г), причем:
Ф(-z)=1-Ф(z), (2.31)
ф(-z)=ф(z) (2.32)
Покажем справедливость соотношения (2.31). Рассмотрим график плотности стандартного нормального распределения (см. рис. 2.3,г). Обозначим площадь под ним левее точки “– z” через S1;площадь между “–z” и “z” –через S2 оставшуюся площадь (правее “z”) – через S3. Тогда, во-первых, из симметричности графика плотности следует, что S1= S3. Во-вторых, S1+S2+S3=1 или S1+(S1+ S2)=1 (вся площадь под графиком плотности рана единице). По смыслу функции распределения S1=Ф(-z), S1+S2=Ф(z). Следовательно, Ф(-z)+Ф(z)=1, откуда и следует равенство (2.31).
Значения нормированной функции (2.29) нормального распределения и значения плотности нормированного распределения (2.30) табулированы и приведены в различных учебниках и справочниках по математической статистике (наиболее подробные таблицы см. [8]).
Геометрически функция Лапласа представляют площадь под кривой f(z) в интервале от -∞ до некоторой конкретной величины z.
Заметим что иногда вместо функции Ф(z) табулируется функция Ф0(z):
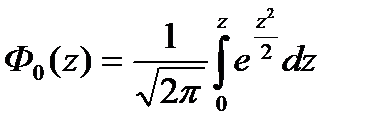 , (2.33)
, (2.33)
равная площади под графиком стандартного нормально распределения от 0 до z (см. рис. 2.3, г).
В силу симметрии:
 (2.34)
(2.34)
Поэтому между функциями существует простая зависимость:
Ф(z) = ½+Ф0(z) (2.35)
Функция Ф0(z) нечетна:
Ф0(-z).=- Ф0(z) (2.36)
В соответствии с (2.21) квантиль zp порядка р, нормированного нормального закона распределения – это такое значение приведенной случайной величины Z, для которого функция распределения принимает значение Р:
Ф(zp)=Р (2.37)
При определении квантили zp необходимо решать задачу, обратную задаче распределения значения функции Лапласа, т.е. по известному значению Р этой функции находить соответствующее ему значение аргумента zp. Для этого можно воспользоваться таблицами для функции, обратной функции Лапласа, т.е. табулированными значениями квантилей нормированного нормального закона распределения.
Для квантили стандартного нормального распределения справедливо следующее равенство:
z1-p=-zp (2.38)
Рассмотрим график плотности стандартного нормального распределения (рис. 2.4). Площадь под графиком левее квантили zp по определению равна р. Значит, площадь правее этой точки равна 1-р. Такая же площадь расположена левее точки z1-p. Итак, площади левее z1-p и правее zр равны. Поскольку график симметричен относительно оси ординат, из этого следует, что эти точки расположены на одинаковом расстоянии от нуля.
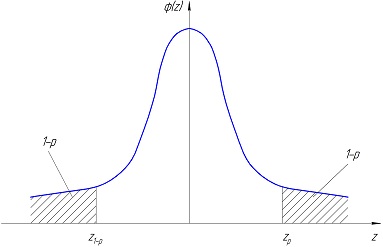
Рис. 2.4.Квантиль стандартного нормального распределения
Зная zp порядка р нормированного нормального закона распределения (Мz=0 и σz2=1), всегда можно найти квантиль хp соответствующего порядка р для нормального распределения с произвольными параметрами Мх и σх2:
xp=Mx+zpσx (2.39)
В ряде случаев важно знать вероятность того, что случайная величина Х, подчиняющаяся нормальному закону распределения, не будет отличаться от своего математического ожидания Mx больше чем на величину 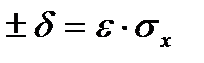 (см. рис.2.3 г):
(см. рис.2.3 г):
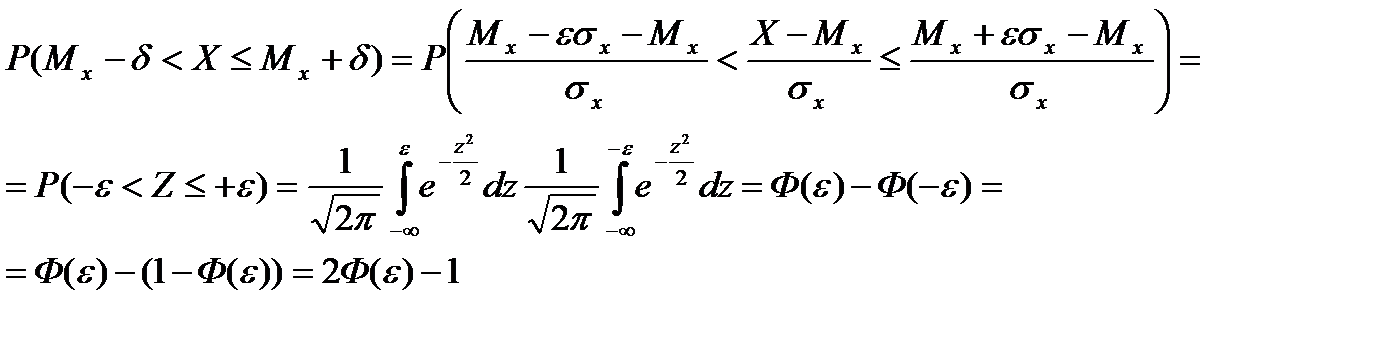
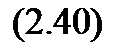
Так, при δ=σx(ε=1) получаем, что Р(Mx+σx<X≤Mx-σx) = 2Ф(1)-1, а поскольку по таблицам (например, см. табл. [8]) Ф(1) = 0,84135, то для случайной величины с нормальным законом распределения вероятность того, что она примет такое значение, которое не будет отличаться от ее математического ожидания более чем на одно среднее квадратическое отклонение, равна 2·0,84135-1 = 0,68. Иными словами, при нормальном распределении примерно 2/3 всех значений случайной величины (отклика) лежит в интервале Mx±σx.
Аналогично можно подсчитать, что интервалу Mx±1,96σx≈Mx±2σx соответствует вероятность 0,95 (Ф(1,96)=0,975002), а интервалу Mx±3σx-0,997 (Ф(3) = 0,99865).
Следовательно, отличие, какого – либо из значений случайной величины с нормальным законом распределения от ее математического ожидания не превосходит утроенного среднего квадратичного отклонения с вероятностью 0,997. Это свойство в математической статистике носит название «правило трех сигм». Чем больше величина интервала Mx±δ, тем с большей вероятностью случайная величина Х попадает в этот интервал.
ОСНОВЫ ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ






