o Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно.
o Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.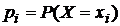 
, причем 
.
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Такая таблица называется рядом распределения дискретной случайной величины.
Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывают значения xi, а по оси ординат—вероятности pi. Полученные точки соединяют отрезками и получают ломаную, которая является одной из форм задания закона распределения дискретной величины.
Пример. Рассмотрим следующую дискретную случайную величину
| X | 1 | 2 | 3 | 4 |
| P | 0,1 | 0,3 | 0,2 | 0,4 |
o Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения 
с вероятностями 
.
| X | 0 | 1 | … | K | … | n |
| P | 
| 
| … | 
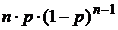
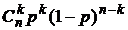
| … | pn |
Пример. µ—число успехов в n испытаниях. µ имеет биномиальное распределение с параметрами (n,p). Обозначают X~B (n,p), т.е. случайная величина Х имеет биномиальное распределение с параметрами (n,p).
o Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения 
с вероятностями 
.
| X | 0 | 1 | … | k | … |
| P | 
| 
| … | 
| … |
Обозначают 
, т.е. случайная величина Х имеет распределение Пуассона с параметром λ. 
Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0<p<1) и, следовательно, вероятность его не появления q=1-p. Испытания заканчиваются как только появится событие А. Таким образом, если событие А появилось в k-ом испытании, то в предшествующих k-1 испытаниях оно не появлялось.
Обозначим через X дискретную случайную величину—число испытаний, которое нужно провести до первого появления события А. Очевидно, возможными значениями случайной величины Х являются натуральные числа.
Пусть в первых k-1 испытаниях событие А не наступало, а в k-ом испытании появилось. Вероятность этого события 
.
o Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 
с вероятностями 
, где q=1-p.
o
| X | 1 | 2 | 3 | … | k | … |
| P | p | qp | q2p | … | qk-1p | … |
Очевидно, что вероятности появления значений 1,2,3… образуют геометрическую прогрессию с первым членом р и знаменателем q (0<q<1).
.
Пример 1. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р=0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.
p=0,6; q=0,4; k=3. 
.
Пример 2. Монета брошена два раза. Написать ряд распределения случайной величины X—числа выпадений «герба».
Решение. Вероятность выпадения «герба» в каждом бросании монеты 
, вероятность того, что «герб» не появится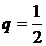 
.
При бросании монеты «герб» может появится либо 2, либо 1, либо 0 раз. Т.е. возможные значения Х таковы: х1=0,х2=1, х3=2.
Найдем вероятности этих возможных значений по формуле Бернулли:
;
;
.
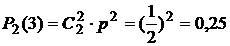Ряд распределения:
| X | 0 | 1 | 2 |
| P | 0,25 | 0,5 | 0,25 |
Пример 3. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут три негодных изделия(n-велико,p-мало).
По условию n=5000, p=0,0002, k=3. По формуле Пуассона 
, искомая вероятность 
.
Простейший поток событий.
Рассмотрим события, которые наступают в случайные моменты времени.
o Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.
Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие.
Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последствия и ординарности.
o Поток событий называется стационарным, если вероятность появления k событий за промежуток времени длительности t зависит только от k и t.
Таким образом, свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени (1, 7), (10, 16), (Т, Т+6) одинаковой длительности t=6 единиц времени равны между собой.
o Поток событий называется ординарным,если за бесконечно малый промежуток времени может появиться не более одного события.
Таким образом, свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события в один и тот же момент времени практически равна нулю.
o Говорят, что поток событий обладает свойством отсутствия последствия, если имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени. Таким образом, свойство отсутствия последствия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, условная вероятность появления k событий на любом промежутке времени, вычисленная при произвольном предположении о том, что происходило до начала рассматриваемого промежутка (т.е. сколько событий появилось, в какой последовательности), равна безусловной вероятности. Следовательно, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.
o Поток событий называется простейшим или пуассоновским, если он стационарный, ординарный, без последствия.
o Интенсивностью потока λ называют среднее число событий, которые появляются в единицу времени.
Если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за промежуток времени длительности t определяется по формуле:
, . Формула Пуассона.
Эта формула отражает все свойства простейшего потока, поэтому ее можно считать математической моделью простейшего потока.
Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 5 минут поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.
По условию λ=2, t=5, k=2. По формуле Пуассона
А) 
—это событие практически невозможно.
Б)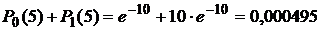 
—событие практически невозможно, т.к. события «не поступило ни одного вызова» и «поступил один вызов»—несовместимы.
В) 
—это событие практически достоверно.
Числовые характеристики дискретных случайных величин.
Как известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание, которое приближенно равно среднему значению случайной величины.
o Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 
.
Если случайная величина Х принимает счетное число значений, то 
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
Пример 1. Найти математическое ожидание случайной величины Х, зная ее ряд распределения.
| X | 3 | 5 | 2 |
| P | 0,1 | 0,6 | 0,3 |
.
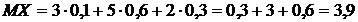Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Случайная величина Х—число появлений события А в одном испытании, может принимать значения х1=1 (событие А наступило) с вероятностью р и х2=0 (А не наступило) с вероятностью q=1-p.
.
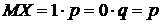Таким образом, математическое ожидание числа появлений события в одном испытании равно вероятности это события.
Свойства математического ожидания:
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:
M(C) = C.
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно,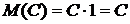 
.
Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
M(CX)= CM(X).
Если случайная величин Х имеет ряд распределения
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Ряд распределения случайной величины СХ
| СХ | Сx1 | Сx2 | … | Сxn | … |
| Р | p1 | p2 | … | pn | … |
Математическое ожидание случайной величины СХ 
.
o Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn 
.
Если взять B1=]-∞, x1[; B2=]-∞, x2[; …; Bn=]-∞,xn[, то 
.
—совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,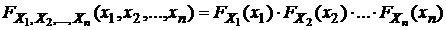 
. Данное равенство также можно взять в качестве определения независимости случайных величин.
Свойство 1. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
.
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Свойство 2. Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:
.
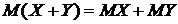Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
Обозначим случайную величину Х—число очков, выпавших на первой кости, через Y обозначим число очков, выпавших на второй кости. Возможные значения этих величин одинаковы и равны 1,2,3,4,5,6, причем вероятность каждого из этих значений равна 
. Найдем математическое ожидание числа очков, которые могут выпасть на первой кости.
. Очевидно, что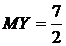 
.
.
Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: 
.
Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события 
. По свойству 4:
.
Согласно примеру 2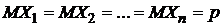 
. Таким образом, получим .
o Дисперсией случайной величины называется число 
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
o Средним квадратическим отклонением случайной величины Х называется число 
.
Пример 4. Найти дисперсию случайной величины Х, которая задана рядом распределения.
| X | 2 | 3 | 5 |
| P | 0,1 | 0,6 | 0,3 |
.
Ряд распределения случайной величины Х2
| Х2 | 4 | 9 | 25 |
| Р | 0,1 | 0,6 | 0,3 |
.
Свойства дисперсии.
Свойство 1. Дисперсия постоянной величины С равна 0.DC=0.
.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
.
.
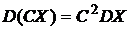Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
.
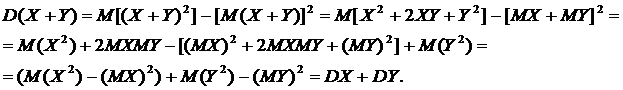
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и не появления события в одном испытании: 
.
Случайная величина Х—число появлений события А в n независимых испытаниях. , где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
.
. Т.к. MX1=p. 
, то 
. Очевидно, что дисперсия остальных случайных величин также равна pq, откуда .
Пример. Проводятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X—числа появлений события в этих испытаниях.
n=10; p=0,6; q=0,4.
.
o Начальным моментом порядка к случайным величинам Х называют математическое ожидание случайной величины Хk:
. В частности, 
, 
.
Пользуясь этими моментами, формулу для вычисления дисперсии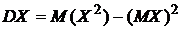 
можно записать так: 
.
Кроме моментов случайной величины Х целесообразно рассматривать моменты отклонения Х- МХ.
o Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ)k.
. В частности
, 
. Следовательно,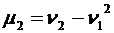 
.
Исходя из определения центрального момента и пользуясь свойствами математического ожидания, можно получить формулы:
.
.
Моменты более высоких порядков применяются редко.
Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
