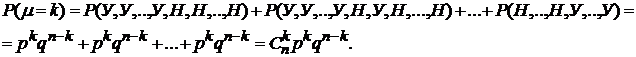Формулы полной вероятности и Байеса.
Теорема 1. Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:
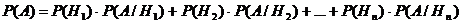, или 
.
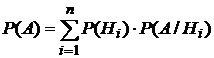Так как события образуют полную группу, то можно записать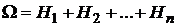 
.
Событие А может произойти только с одним из событий Hi, i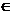 
{1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей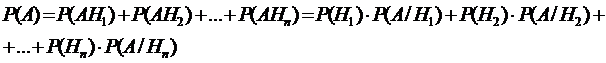 
Пример. Имеются 2 урны. В первой—3 белых и 5 черных шаров, во второй—4 белых и три черных. Из первой наудачу взят один шар и переложен во вторую урну. После этого из второй урны был извлечен наудачу шар. Какова вероятность, что он белый?
Событие А—из второй урны извлечен шар;
Н1—из первой урны во вторую переложен белый шар
Н2—из первой урны во вторую переложен черный шар.
.
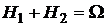
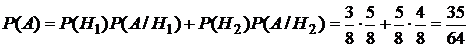Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn, образующие полную группу, называются гипотезами.
Теорема 2. Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:
, 
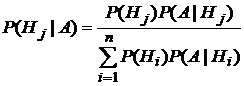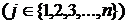
Доказательство: По теореме умножения вероятностей
.
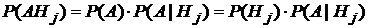Отсюда находим вероятность
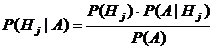. Остается в знаменателе подставить вместо 
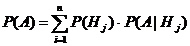—формула полной вероятности.
Пример. Рассмотрим предыдущий пример с учетом того, что из второй урны вынули белый шар. Найти вероятность того, что из первой урны вынули белый шар. Нужно найти P(H1|A).
.
.
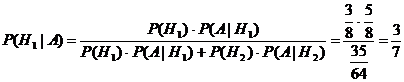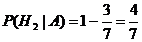Замечание. При применении формулы Байеса вероятности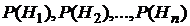 
называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез.
Тема 1.4 Последовательность независимых испытаний
1.4.1 Схема независимых испытаний Бернулли.
1.4.2 Вероятность появления определенного числа успехов.
1.4.3 Наиболее вероятное число успехов.
Схема независимых испытаний Бернулли
Схема независимых испытаний Бернулли
Полиноминальное распределение.
Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей.
, 
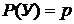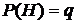, p+q=1.
Предположим, что мы производим независимо друг от друга n таких испытаний.
o Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
Элементарным исходом будет являться:
(w1,w2,…,wn),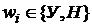 
.
Всего таких исходов 2n.
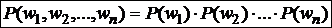. (1)
Формула (1) показывает, что события независимы.
Обозначим через µ число успехов в n испытаниях Бернулли.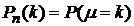 
— вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие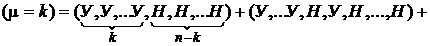 
.
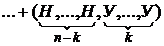По теореме сложения получим
