Пусть имеется множество из n элементов a1, a2,an. Будем рассматривать выборку объема k 
из n элементов. Все выборки можно классифицировать по 2 признакам:
1. упорядоченные и неупорядоченные.
2. с возвращением и без возращения.
Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными.
Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов отождествляются.
Пример. Возьмем множество из трех элементов {1,2,3}. Выбираем k=2.
| (1,1);(1,2);(1,3); (2,1);(2,2);(2,3); (3,1);(3,2);(3,3); | (1,1);(1,2);(1,3); (2,2);(2,3); (3,3); | С возвращением |
| (1,2);(1,3); (2,1);(2,3); (3,1);(3,2); | (1,2);(1,3); (2,3); | Без возвращения |
| упорядоченная | Неупорядоченная | выборка |
Составим общую таблицу числа выборок:
| 
| С возвращением |
| 
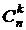
| Без возвращения |
| упорядоченная | Неупорядоченная | Выборка |
Упорядоченная выборка с возвращением 
). Каждый элемент выборки может принимать n значений, т.е. число выборок 
. Упорядоченная выборка без возвращения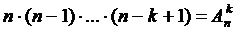 
.
o Упорядоченная выборка без возвращения называется размещением. Число размещений 
.
Пример. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах.
n=113.
, 
.
o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке.
Pk -число перестановок из k элементов. 
, поскольку 0!=1.
o Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через 
.
. 
, где 
.
.
Свойства сочетаний:
1. 
.
2. 
.
3. 
.
4. 
.
Геометрические вероятности.
Предположим, что на числовой оси имеется некоторый отрезок [a,b] и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на 
.
—геометрическая вероятность на прямой.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
— геометрическая вероятность на плоскости.
Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством:
—геометрическая вероятность в пространстве.
Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности.
Произведение событий
Свойства вероятности.
Свойство 1. Вероятность невозможного события равна 0, т.е. 
. 
.
Свойство 2. Вероятность достоверного события равна 1, т.е. 
, 
.
Для любого события 
. 
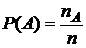, т.к. 
, то 
и следовательно 
.
Сумма событий
Свойство 3.
Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
.
.
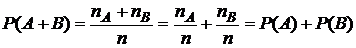