Свойство 1. Относительная частота произвольного события А. 
.
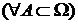Свойство 2. Относительная частота достоверного события равна 1. 
.
Свойство 3. (Аддитивность) Относительная частота суммы несовместимых событий 
ТЕМА1.2 Аксиоматическое определение вероятности
1.2.1 Вероятностная модель эксперимента
1.2.2 Произведение событий
1.2.3 Сумма событий
1.2.4 Алгебра событий
1.2.1 Вероятностная модель эксперимента
Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.
o Событие—это подмножество Ω, принадлежащее классу F. Любому 
ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы:
Аксиома 1.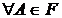 
Аксиома 2. 
,т.е. вероятность достоверного события равна 1.
Аксиома 3. (счетной аддитивности) Если 
и 
, то 
(для несовместимых событий).
Дискретные пространства элементарных исходов.
Классическое определение вероятности.
o Бесконечное множество называется счетным, если элементы этого множества можно занумеровать числами натурального ряда (натуральными числами).
Все другие бесконечные множества называются несчетными. Примером несчетного множества может служить [а,b], счетного N.
o Пространство элементарных исходов называется дискретным, если оно конечно или счетно, т.е. 
или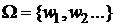 
.
Любому элементарному исходу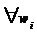 
ставится в соответствие число 
, так что при этом 
. Т.е. 
o Вероятностью события А называется число 
.
Пример. Бросаем игральную кость 
—дискретное пространство элементарных исходов. 
. Р (выпадает нечетное количество очков)= 
Сделаем следующие предположения:
1. Пространство элементарных исходов 
—конечно.
2. Все элементарные исходы равновозможны (равновероятны), т.е.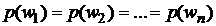 
. Тогда получим 
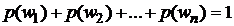, т.к. слагаемые равны, то имеем 
, т.е. 
, где 
. Рассмотрим некоторые события 
, где k≤n. Вероятность события. 
o Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятностью события А называется отношение числа элементарных исходов, благоприятствующих событию А к общему числу элементарных исходов: 
.
Это классическое определение вероятности.
Примеры:
1. Бросается игральная кость. Какова вероятность выпадения нечетного числа очков?
, n=6; 
, k=3; 
.
2. Бросаются две монеты. Какова вероятность того, что хотя бы на одной выпадет герб?
, 
, 
.
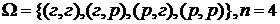3. Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна семи?
, n=36;
, k=6;
.
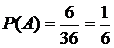Элементы комбинаторики.
Лемма 1. Из m элементов а1,…,аm первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (аi, bj), содержащих по одному элементу из каждой группы.
Доказательство:
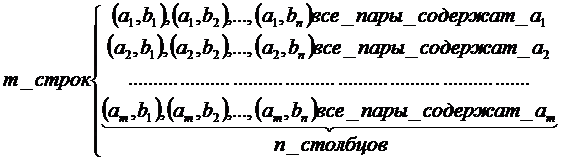
Всего имеем m∙n пар.
Пример. В колоде 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт. Итого n=4∙9=36.
Лемма 2. Из n1 элементов первой группы a1, а2,…, аn1,
n2 элементов второй группы b1, b2,…, bn2,
n3 элементов k-ой группы x1, x2,…, xnk
можно составить ровно n1∙ n2∙…∙nk различных упорядоченных комбинаций вида 
, содержащих по одному элементу из каждой группы.
1. При k=2 утверждение выполняется (Лемма 1).
2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов 
. Рассмотрим комбинацию 
как 
и 
. Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1.
Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216.
