Признаки сходимости числовых рядов c положительными членами

 

Числовой ряд называется рядом с положительными членами или просто положительным рядом, если все члены ряда

 

u ₁ + u ₂ + u ₃ +... + u_n  +...

 

больше нуля 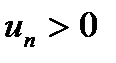. Рассмотрим признаки сходимости для положительных рядов.

Первый признак сравнения. Пусть даны три ряда:

 ряд, сходимость которого надо определить    

 

u ₁ + u ₂ + u ₃ +... + u_n  +... (7.4)

 

сходящийся ряд v ₁ + v ₂ + v ₃ +... + v_n  +...                                           (7.5)

 

расходящийся ряд w ₁ + w ₂  + w ₃ +... + w_n +...                          (7.6)                                       

 Тогда:

а) если начиная с некоторого номера n, выполняется условие    

u_n £ v_n (7.7)

 

то из сходимости ряда (7.5) следует сходимость ряда (7.4);

б) если, начиная с некоторого номера n, выполняется условие

 u_n ³ w_n     (7.8)

то из расходимости ряда (7.6) следует расходимость ряда (7.4).

Доказательство.

 а) Обозначим частичные суммы рядов

 

S_n = u ₁ + u ₂  + u ₃ +... + u_n

Ф _n = v ₁ + v ₂ + v ₃ +... + v_n

 

в силу условия (7.7) имеем S_n £Ф _n.

По условию ряд (7.5) сходится, т.е. 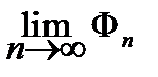 = Ф, следовательно

Ф³Ф _n ³ S_n.

Это означает, что последовательность частичных сумм S_n возрастает (в силу положительности ряда (7.4)) и ограниченна сверху величиной Ф. Поэтому 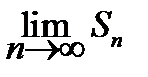 существует и конечен, а ряд (7.4) сходится.

б) Обозначив частичную сумму ряда (7.6) за W_n

W_n = w ₁ + w ₂ + w ₃ +... + w_n,

в силу (7.8) имеем S_n ³ W_n.

По условию ряд (15.6) расходится, т.е. 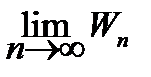= ¥, следовательно

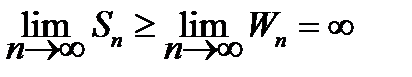
и ряд (15.4) расходится.

 

Второй признак сравнения. Пусть даны два ряда

 

u ₁ + u ₂ + u ₃ +... + u_n +...                                                                          (7.9)

v ₁ + v ₂ + v ₃ +... + v_n  +...                                                            (7.10)

 

и можно указать такие постоянные числа k₁ > 0 и k₂ > 0, что, начиная с некоторого достаточно большого n,

 

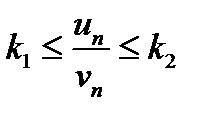                                                                                           (7.11)

Тогда ряды (7.9) и (7.10) одновременно сходятся или одновременно расходятся.

Доказательство. Из (7.11) следует, что

 

k ₁ v_n £ u_n £ k ₂ v_n.                                                    (7.12)

 

Если ряд (7.9) сходится, то из левого неравенства (7.12) по первому признаку сравнения вытекает сходимость ряда

 

k ₁ v ₁ + k ₁ v ₂  + k ₁ v ₃ +... + k ₁ v_n +...

Из сходимости этого ряда, по свойству 2, вытекает и сходимость ряда (7.10).

Предположим теперь, что ряд (7.9) расходится. В этом случае расходится и ряд

 

 

Из правой части (7.11) следует, что

Следовательно, по первому признаку сравнения, ряд (7.10) также расходится.

Следствие (предельный признак сравнения). Если для рядов (7.9) и (7.10) выполняется условие

 = r <¥, где r ¹ 0,                                                         (7.13)

 

то эти ряды сходятся или расходятся одновременно.

 

Для сравнения обычно используются следующие эталонные ряды.

Геометрический ряд (ряд геометрической прогрессии)

 

a + aq + aq ² +... + aq^{n -1} +....

 

Геометрический ряд сходится при условии q < 1. В противоположном случае (q ³ 1) ряд расходится. Например, ряд

,

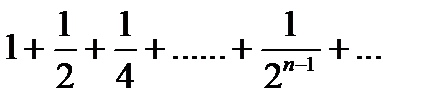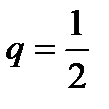
сходится, а ряд

 

1 + 2 + 4 +... + 2 ^{n -1} +..., q = 2

 

расходится. Можно также сказать, что этот ряд расходится потому, что не выполнено необходимое условие сходимости ряда.

Обобщенным гармоническим рядом называется ряд

 

 

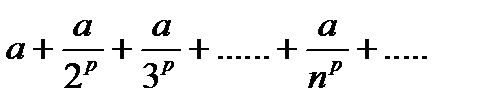
Этот ряд сходится при p > 1 и расходится при p £ 1.

Например, ряд

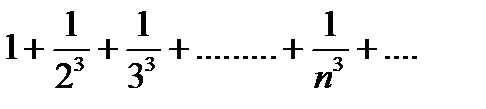- сходится, а ряд

- расходится.

Обобщенный гармонический ряд при p = 1 называют просто гармоническим рядом:

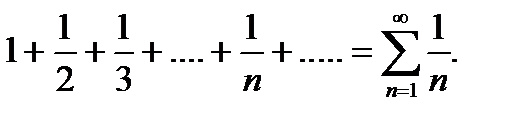
Гармонический ряд расходится!

Действительно, сгруппируем члены ряда по степеням 2

 

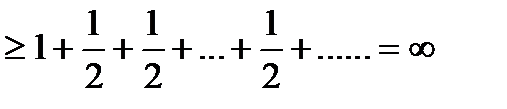
Так как сумма слагаемых в каждой скобке больше .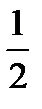

Пример. Исследовать сходимость ряда

 

Решение. Сравним общий член этого ряда с геометрическим рядом 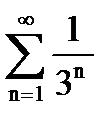, который сходится. Так как

 

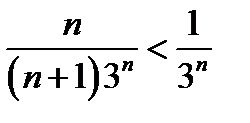
то, по первому признаку сравнения исследуемый ряд сходится.

Пример. Исследовать сходимость ряда

 

 

Решение. Сравнивая общий член этого ряда с общим членом гармонического ряда

 

 

заключаем, что этот ряд также расходится (по первому признаку сравнения).

Пример. Исследовать сходимость ряда

 

 

Решение. Воспользуемся следствием из второго признака сравнения, сравним с расходящимся гармоническим рядом

При вычислении предела мы использовали правило Лопиталя: предел отношения двух функций с неопределенностью или  равен пределу

отношения производных 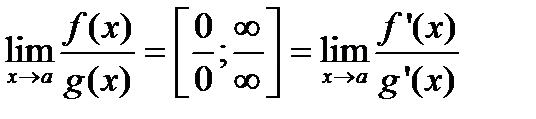. Поэтому

.

 

Сравниваемые ряды ведут себя одинаково, поэтому заключаем, что исследуемый ряд расходится (т.к. гармонический ряд расходится).

Пример. Исследовать сходимость ряда

 

 

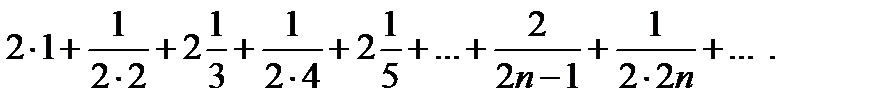
Решение. Рассмотрим отношение членов этого ряда к соответствующим членам гармонического ряда:

- при нечетном n имеем ,

- при четном n имеем     .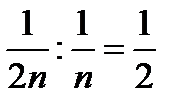

Следовательно, отношение u_n / v_n ни к какому пределу не стремится. Однако при всех n оно заключено между 1/2 и 2. Поэтому согласно второму признаку сравнения исследуемый ряд ведет себя так же, как и гармонический, т.е. расходится.

Признак Даламбера сходимости рядов с положительными членами. Пусть дан положительный ряд

 

u ₁ + u ₂ + u ₃ +... + u_n  +... (7.14)

 

Если отношения последующего члена ряда u_n к предыдущему u_{n -1}, начиная с некоторого значения n = N, удовлетворяет неравенству

 

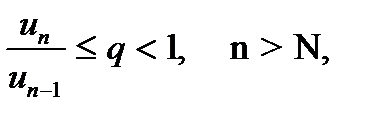                                                                                 (7.15)

то ряд (7.14) сходится.

Если же, начиная с некоторого N, имеем

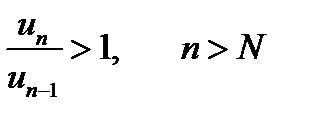                                                                                       (7.16)

то ряд (7.14) расходится.

Доказательство. Пусть имеет место соотношение (7.15), которое выполняется для всех n. Тогда

 

u_n £ u_{n -1} q, u_{n -1} £ u_{n -2} q,..., u ₂ £ u ₁ q.

 

Отсюда, подводя почленную подстановку, получаем

 

u_n £ u ₁ q^{n -1}        

^.

Это неравенство означает, что общий член ряда (7.14) не превосходит соответствующего члена сходящегося (q < 1) геометрического ряда. В силу первого признака сравнения ряд (7.14) сходится.

Пусть имеет место соотношение (7.16). Тогда

 

u ₁ < u ₂ < u ₃ <...< u_{n -1} < u_n <...,

 

т.е. члены ряда не убывают по мере возрастания n. Следовательно, не выполнено необходимое условие сходимости ряда и ряд (7.14) расходится. Если условие выполняется начиная с некоторого номера n, то это означает, что сходится остаток ряда, а по первому свойству сходится и сам ряд.На практике удобнее пользоваться предельным признаком Даламбера, формулировку которого дадим в виде следствия.

Следствие. (Предельный признак Даламбера). Если

 

,

 

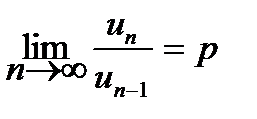то при p< 1 ряд (7.14) сходится, при p> 1 этот ряд расходится.

Пример. Исследовать сходимость ряда

 

 

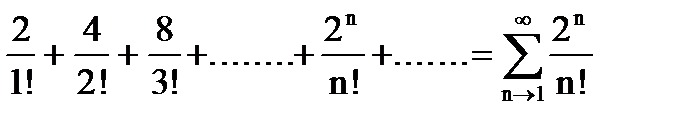
Решение. Рассмотрим предел отношения

 

 

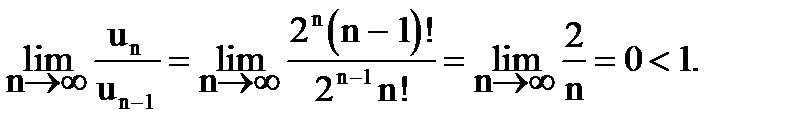
Следовательно, исследуемый ряд сходится.

Замечание. Если 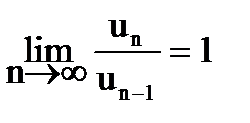 , то признак Даnамбера не дает ответа на вопрос о сходимости ряда. В этих случаях надо привлекать другие признаки сходимости ряда.

 

Знакочередующиеся ряды

 

Знакочередующимися рядами называются ряды вида

 

u ₁- u ₂ + u ₃ - ... + (-1) ^{n +1} u_n  +...                                                     (7.17)

 

где все u_n > 0.

 

Сходимость таких рядов исследуется по теореме Лейбница: если в знакочередующемся ряде (7.17) все члены таковы, что u ₁ > u ₂ >…> u _n >.... и 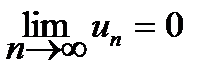, то ряд (7.17) сходится, его сумма положительна и не превосходит первого члена ряда u ₁.

Доказательство. Возьмем сумму четного числа первых членов S _{2 m ,} которая положительна.

 

S _{2 m} = (u ₁ - u ₂ ) + (u ₃ - u ₄ ) +......+ (u _{2 m -1} – u _{2 m} ) > 0,  

 

так как выражение в каждой скобке больше нуля. S _{2 m} возрастает при росте m, т.к. S _{2 m} = S _{2(m -1)} + (u _{2 m -1} – u _{2 m} ) > S _{2(m -1)}.

С другой стороны

 

S _{2 m} = u ₁ - (u ₂  - u ₃ ) - (u ₄ – u ₅)......- (u _{2 m -2} - u _{2 m -1}) – u _{2 m} < u ₁.

 

т. е. при росте mS _{2 m} возрастает и ограничена сверху. Следовательно, имеет предел S = 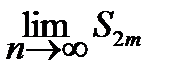 .Нечетные суммы будут иметь тот же предел. Действительно

S _{2 m +1} = S _{2 m} + u _{2 m +1}

 

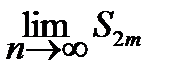 +  = S + 0 = S.

 

Четные и нечетные суммы ряда имеют тот же предел, следовательно, ряд сходится. Теорема доказана.

По знакочередующемуся ряду можно построить соответствующий ему положительный ряд u ₁ + u ₂  + u ₃ + u ₄ + …+ u_n +.... Если такой положительный ряд сходится, то знакочередующийся ряд называют абсолютно сходящимся, в противном случае ряд называют условно сходящимся. В абсолютно сходящемся ряде члены ряда можно переставлять без потери сходимости, в условно сходящемся ряде перестановка членов ряда запрещена, т.к. она может привести к потере сходимости. 

 

Степенные ряды

 

Степенным рядом  по степеням x называется функциональный ряд вида

 

C ₀ + C ₁ x + C ₂ x ² +... C_nxⁿ +... = 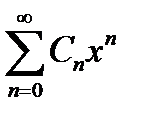,                                         (7.18)

где C ₀, C ₁,... C_n,... не зависят от переменной x и называются коэффициентами этого ряда.

Если при x = x ₀ числовой ряд 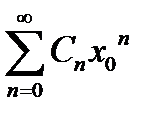сходится, то x ₀ называется точкой сходимости ряда (7.18). Областью сходимости  ряда называется множество всех точек сходимости этого ряда.

Степенной ряд (7.18) всегда сходится, по крайней мере, в точке x =0.

 

Степенной ряд (7.18) сходится в точке x ₀ абсолютно, если сходится ряд образованный из модулей членов числового ряда

 

½ C ₀½+ ½ C ₁x₀½ + ½ C ₂ x ₀²½+... ½ C_nx ₀ ⁿ ½+....                            (7.19)

 

Найдем область сходимости ряда (7.18), используя признак Даламбера

для положительных числовых рядов. По этому признаку ряд (7.19) сходится, если

 

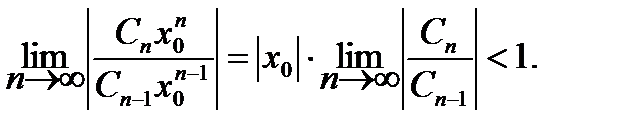
Следовательно, по признаку Даламбера ряд (4.54) заведомо сходится при

 

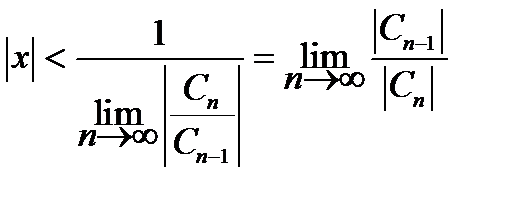и расходится при .

 

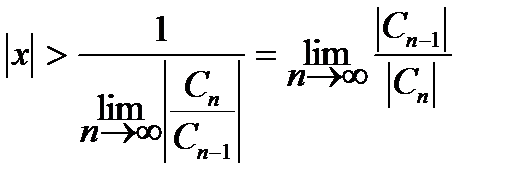Величина  

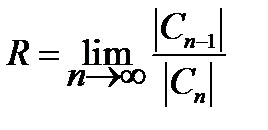 (7.20)

называется радиусом сходимости  ряда степенного ряда. Ряд заведомо сходится в интервале ½ x ½< R или - R < x < R, который называется интервалом сходимости.

Признак Даламбера ничего не говорит о сходимости ряда в точках х = В этих точках сходимость ряда исследовать отдельно.

Исследовать степенной ряд на сходимость означает найти его интервал сходимости и установить сходимость или расходимость ряда в граничных точках интервала, т.е. при x = R и x = - R.

Пример. Исследовать на сходимость степенной ряд

Решение. Используя формулу (7.20), имеем

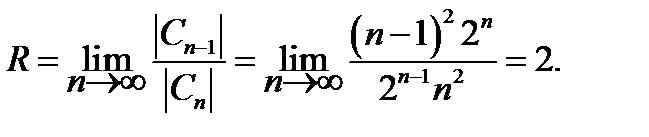
Интервал сходимости данного ряда характеризуется неравенством ½ x ½< 2. Исследуем сходимость ряда в граничных точках x =±2. Очевидно, что

.

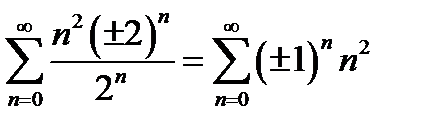Оба эти ряда расходятся, так как не выполняется необходимое условие сходимости численных рядов. Следовательно, область сходимости данного степенного ряда совпадает с интервалом сходимости.

Пример. Найти область сходимости следующего ряда

1 + x + 2² x ²  + 3³ x ³ +... + nⁿxⁿ +... = 1 + .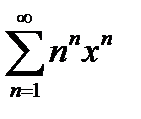

Решение. По формуле (7.20) найдем

.

 

Следовательно, ряд сходится только в одной точке x =0.

Пример. Найти область сходимости следующего ряда:

 

.

 

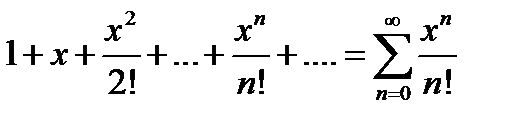Решение. Так как

 

 

то ряд сходится при всех конечных значениях x, т.е. -¥< x <¥.