Закон распределения случайной величины представляет собой некоторую функцию, которая полностью описывает случайную величину с вероятностной точки зрения. Однако при решении многих практических задач нет необходимости характеризовать случайную величину полностью, исчерпывающим образом. Во многих случаях достаточно бывает указать отдельные числовые параметры, в определенной степени характеризующие наиболее существенные особенности распределения случайной величины: например, какое-то среднее значение, около которого группируются возможные значения случайной величины; какое-либо число, характеризующее степень разбросанности этих значений относительно среднего и т.д.
Такие характеристики, которые в сжатой форме выражают наиболее существенные особенности распределения, называют числовыми характеристиками случайной величины. К их числу относятся математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание
Математическое ожидание случайной величины указывает на некоторое ориентировочное значение, вокруг которого группируются все значения случайные величины.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайные величины:

Для непрерывных случайных величин

где:  – непрерывно изменяющаяся случайная величина,
– непрерывно изменяющаяся случайная величина,
 – элемент вероятности.
– элемент вероятности.
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно этой постоянной:

2. Постоянный множитель можно выносить за знак математического ожидания:

3. Математическое ожидание алгебраической суммы случайных величин:

4. Математическое ожидание произведения независимых случайных величин:

5. Математическое ожидание отклонения случайной величины от её математического ожидания равно нулю:

Математическое ожидание характеризуетположение случайной величины на числовой оси, т.е. указывает некоторое среднее ориентировочное значение, около которого группируются все возможные значения случайной величины.
Кроме математического ожидания на практике иногда применяют и другие характеристики положения – моду и медиану случайной величины.
Дисперсия
С помощью этой характеристики судят о рассеянии случайной величины относительно математического ожидания.
Из свойства №5 математического ожидания очевидно, что выбор в качестве меры рассеяния математического ожидания отклонения случайной величины от её математические ожидания не дает никакого результата. Поэтому в качестве меры рассеяния случайной величины берут математическое ожидание квадрата отклонения случайной величины от её математического ожидания, которое называют дисперсией случайной величины:

Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от её математические ожидания на соответствующие вероятности:

Для непрерывной случайной величины:

Свойства дисперсии
1. Дисперсия постоянной величины равна 0:

2. Постоянный множитель можно вынести за знак дисперсии, предварительно возведя его в квадрат:
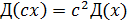
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
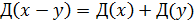
5. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайные величины и квадратом её математические ожидания.







