| ПЛАН: | 4.1. Основные понятия дифференциальных уравнений. |
| 4.2. Дифференциальные уравнения первого порядка с разделяющимися переменными и метод их решения. | |
| 4.3. Составление и решение дифференциальных уравнений на примерах задач физического, химического и медико-биологического содержания. |
Дифференциальные уравнения используются при изучении явлений и процессов во всех областях знаний, в том числе и в медицине. Сформулировав задачу на языке дифференциальных уравнений, специалист–медик получает готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения. Кроме того, дифференциальные уравнения являются одним из средств математического моделирования. Пользуясь ими, устанавливается связь между переменными величинами, характеризующими данный процесс или явление.
4.1. ОСНОВНЫЕ ПОНЯТИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дифференциальным уравнением называется уравнение, связывающее независимую переменную 
, искомую функцию 
и её производные 
. Общий вид дифференциального уравнения:
или
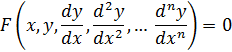
Порядок дифференциального уравнения определяется порядком наивысшей производной, входящей в данное уравнение:
- дифференциальное уравнение первого порядка.
- дифференциальное уравнение второго порядка.
Дифференциальное уравнение называется полным, если оно содержит в себе свободный член, производные, начиная с производной нулевого порядка, затем производных первого, второго и т.д. порядков. Если же один из этих членов отсутствует, то уравнение называется неполным.
Дифференциальное уравнение называется приведённым, если в его правой части стоит ноль.
Дифференциальное уравнение называется обыкновенным, если искомая функция 
есть функция одного аргумента.
Решением или интегралом дифференциального уравнения называется всякая функция , которая будучи подставлена в дифференциальное уравнение (вместе со своими производными) превращает его в тождество.
Всякое решение, которое содержит столько произвольных постоянных, каков порядок уравнения называется общим решением. Решение, полученное из общего решения, путём задания произвольным постоянным определённых численных значений называется частным решением. На практике частное решение получается из общего решенияне прямым заданием значений произвольных постоянных, а исходя из тех условий, которым должно удовлетворять искомое частное решение.
