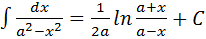Пусть дана функция 
-переменных:
В этом случае вводится понятие частной производной:
Частной производной функции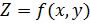 
по аргументу 
называется предел отношения приращения функции, когда изменяется , к приращению аргумента 
, когда приращение аргумента стремится к нулю 
Соответственно частная производная по 
обозначается 
.
Если частную производную от функции 
по умножить на ее дифференциал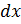 
, то получим частный дифференциал по аргументу :
Частный дифференциал по будет равен:
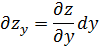
Полный дифференциал для функции двух переменных 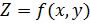определяется по формуле:
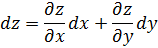
Например:
Найти полный дифференциал функции:
.
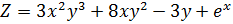Решение:
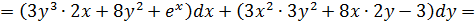
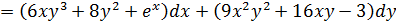
1.10. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА В ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЯХ
При достаточно малых 
выполняется условие: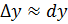 
.
Учитывая, что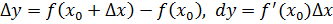 
, получаем
, откуда
(*)
Например:
1. Вычислить 
.
, тогда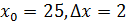 
. Применяя формулу (*), получаем: 
2. Вычислить 
.
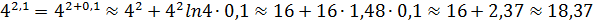
3. Вычислить 
.
4. Вычислить 
.
2.НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
| ПЛАН: | 2.1. Первообразная функция и неопределённый интеграл. |
| 2.2. Свойства неопределённого интеграла. | |
| 2.3. Таблица основных интегралов. | |
| 2.4. Простейшие методы интегрирования: а) непосредственное интегрирование б) метод постановки в) интегрирование по частям |
Интегральное исчисление является составной частью математического анализа и применяется при решении многих задач химии, биологии именно в тех случаях, когда по известной производной требуется найти вид самой функции.
2.1. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ
Процесс дифференцирования т.е. нахождение производной или дифференциала функции, с физической точки зрения, сводится к следующему: зная закон движения материальной системы можно определить мгновенное значение скорости в данной точке траектории её движения. 
геометрической точки зрения, этот процесс состоит в нахождении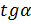 
угла наклона касательной, проведённой к графику функции в данной точке.
Но часто ставится и обратная задача, т. е. необходимо определить закон движения материальной системы, зная её скорость или по 
угла наклона касательной найти соответствующую функцию. Для решения этой задачи вводится понятие неопределённого интеграла, а сам процесс решения называется интегрированием.
Другими словами: если процесс дифференцирования состоит в нахождении производной данной функции, топроцесс интегрирования - это нахождение функции по её производной или дифференциалу.
Введём понятие первообразной функции:
Функция 
, имеющая функцию 
своей производной или 
своим дифференциалом, называется первообразной данной функции:
Пример 1. Основная задача механики состоит в нахождении положения, т.е. координат движущегося тела или материальной точки в любой момент времени. Для прямолинейного равноускоренного движения с начальной скоростью зависимость координаты от времени определяется следующей формулой:
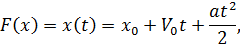
где: 
- начальная координата
- начальная скорость
- ускорение
Тогда мгновенная скорость будет: 
При любых значениях выражение для скорости, т.е. производной остаётся одним и тем же.
Пример 2. Найти производные следующих функций:
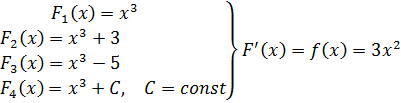
Таким образом, одной производной или одному дифференциалу соответствует не одно, а множество первообразных.
Совокупность всех первообразных функций для дифференциала 
называется неопределённым интегралом и обозначается:
где,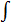 
–знак неопределённого интеграла
– подынтегральное выражение
– подынтегральная функция
– первообразная функция
– постоянная интегрирования
–решение неопределенного интеграла или совокупностьпервообразных.
2.2. СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Производная от неопределённого интеграла равна подынтегральной функции:
2. Дифференциал от неопределённого интеграла равен подынтегральному выражению:
3. Интеграл от дифференциала функции равен самой функции, сложенной с произвольной постоянной:
4. Постоянный множитель можно вынести за знак интеграла:
5. Интеграл алгебраической суммы функций равен алгебраической сумме интегралов этих функций:
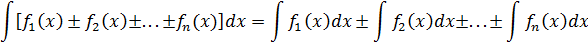
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
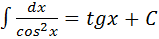
10. 
11. 
12. 
13. 
14. 
15. 
