Метод непосредственного интегрирования
Этот метод основан на использовании свойств неопределённого интеграла и приведении подынтегрального выражения к табличной форме.
Например:
1. 
2. 
3. 
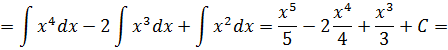
4. 
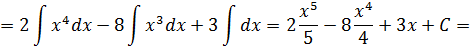
Каждое промежуточное интегрирование даёт свою произвольную 
. Алгебраическая сумма произвольных постоянных будет так же произвольной постоянной. Поэтому в окончательном результате принято ставить одну произвольную постоянную.
Метод подстановки (замены переменной)
Этот метод основан на введении новой переменной. В интеграле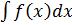 
сделаем подстановку:
;
;
тогда:
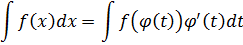
Например:
1. 
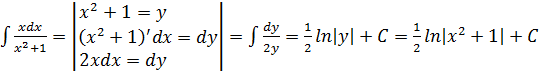
2. 
3. 
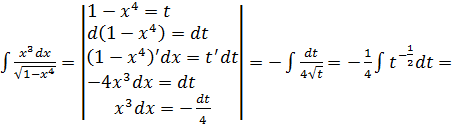
Интегрирование по частям
Пусть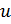 
и 
- дифференцируемые функции, то: 
, откуда
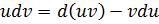
проинтегрируем это выражение
или
Например:
1) 
2) 
3) 
3.ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
| ПЛАН: | 3.1. Понятие определённого интеграла и его геометрический смысл. |
| 3.2. Связь между определённым и неопределённым интегралами. | |
| 3.3. Свойства определённого интеграла. | |
| 3.4. Основные методы нахождения определённого интеграла. | |
| 3.5. Приложения интегрального исчисления (вычисление площадей плоских фигур). |
При математических расчётах часто требуется найти приращение первообразной функции при изменении её аргумента в заданных пределах. Такую задачу приходится решать при вычислении площадей и объёмов различных фигур, при определении среднего значения функции, при вычислении работы переменной силы. Эти задачи могут быть решены вычислением соответствующих определённых интегралов.
3.1. ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Рассмотрим задачу о нахождении площади криволинейной трапеции.
Пусть дана некоторая функция 
, график которой изображён на рисунке.
На оси 
выберем точки 
и 
и восстановим из них перпендикуляры до пересечения с кривой. Фигура, ограниченная кривой, перпендикулярами и осью называется криволинейной трапецией. Разобьём интервал 
на ряд небольших отрезков. Выберем произвольный отрезок 
. Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:
.
Тогда площадь всех достоверных прямоугольников в интервале будет равна:
Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:
Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.
Интегральная сумма есть сумма произведения приращения аргумента на значение функции 
, взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.
Функция 
в некотором интервале от 
до 
интегрируема, если существует такое число 
, к которому стремится интегральная сумма при 
. В этом случае число называют определённым интегралом функции 
в интервале :
где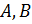 
– область интегрирования (
– нижний предел интегрирования, 
– верхний предел интегрирования).
Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале и осью абсцисс.
3.2. СВЯЗЬ МЕЖДУ ОПРЕДЕЛЁННЫМ И НЕОПРЕДЕЛЁННЫМ ИНТЕГРАЛАМИ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА.
Неопределённый интеграл - это совокупность первообразных функций.
Определённый интеграл - это число.
Связь между ними задаётся формулой Ньютона-Лейбница.
Теорема. Значение определённого интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределами интегрирования:
Например:
1. 
2. 
3.3. СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Определённый интеграл не зависит от обозначения переменной интегрирования:
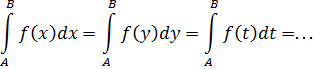
2. Определённый интеграл от суммы конечного числа непрерывных функций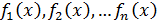 
, заданных на отрезке равен сумме определённых интегралов от слагаемых функций:
3. Постоянный множитель можно вынести за знак интеграла:
4. Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит свой знак на противоположный:
5. Если 
, то
6. Если отрезок интегрирования разбить на две части 
и 
, то:
7. Если подынтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, т.е. если 
, то
8. Значение определённого интеграла заключено между произведениями наибольшего и наименьшего значений подынтегральной функции на длину интервала интегрирования:
где 
– наибольшее и наименьшее значение функции на отрезке.
9. Определённый интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке 
отрезка интегрирования на длину отрезка 
:
где 
- среднее значение функции в интервале.
3.4. ОСНОВНЫЕ МЕТОДЫ НАХОЖДЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Непосредственное интегрирование
1) 
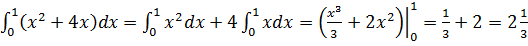
2) 
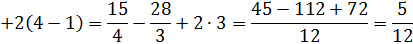
2. Метод подстановки
1) 
2) 
3. Интегрирование по частям
1) 
