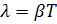Экспериментальное Определение коэффициента корреляции для линейной зависимости.

Для экспериментального изучения зависимости между двумя величинами и производят некоторое количество независимых испытаний:

Результат -того измерения дает пару значений .

Вычисления производят в следующем порядке:

1. Вычисляют выборочные средние:

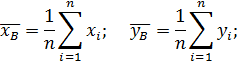
2. Вычисляют выборочные средние квадратические отклонения:

3. Вычисляют оценку ковариации.

4. Вычисляют коэффициент корреляции

Задача 1. Рассчитать коэффициент парной линейной корреляционной зависимости, сделать вывод по знаку коэффициента корреляции и о степени связи следующих величин.

Объем крови (л)	4,22	4,69	5,04	4,34	4,22	4,8	4,45	4,69	4,92	4,57
Вес , (кг)	52	73	86	54	50	74	61	69	80	66

Решение. Определим выборочные средние:

Составим таблицу:

											S
(л)	-0,37	0,1	0,45	-0,25	-0,37	0,21	-0,14	0,1	0,33	-0,0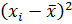2
(л²)	0,14	0,01	0,20	0,06	0,14	0,04	0,02	0,01	0,11	0,0004	0,73
(кг)	-14,5	6,5	19,5	-12,5	-16,5	7,5	-5,5	2,5	13,5	-0,5
(кг²)	210,2	42,2	380,25	156,25	272,25	56,25	30,25	6,25	182,2	0,25	1336,5
(лкг)	5,36	0,65	8,77	3,125	6,10	1,57	0,77	0,25	4,45	0,01	31,05

Вычислим выборочные среднеквадратические отклонения:

Вычислим оценку ковариации:

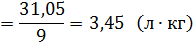
Вычислим коэффициент корреляции:

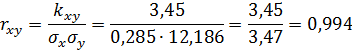
Вывод: С увеличением веса человека объем циркулирующей крови увеличивается, причем связь между этими параметрами является сильной.

Глава 2. МЕДИЦИНСКАЯ ФИЗИКА

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

ПЛАН:	1.1. Свободные механические колебания (незатухающие и затухающие).
	1.2. Вынужденные колебания. Резонанс.
	1.3. Автоколебания.
	1.4. Механические волны. Уравнение механической волны.
	1.5. Поток энергии и интенсивность волны.
	1.6. Ударные волны.
	1.7. Эффект Доплера и его использование для медико-биологических исследований.

СВОБОДНЫЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ (НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ)

Колебаниями называются повторяющиеся движения, или изменения состояние (например: движение маятника, переменный электрический ток, работа сердца, изменения объема грудной клетки и брюшной полости при вдохе и выдохе, колебания стенок артерий при распространении пульсовой волны и т.п.). Всем колебаниям, независимо от их природы, присущи общие закономерности, которые описываются аналогичными математическими уравнениями. Колебания распространяются в среде в виде волн.

Свободными колебаниями называется такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии.

Наиболее простой формой колебаний являются гармонические, которые мы рассмотрим на примере механических колебаний.

Незатухающие колебания

Пусть тело массой прикреплено к пружине. Возникающая при растяжении пружины упругая сила определяется по закону Гука.

где, 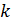-коэффициент пропорциональности между силой и смещением (жёсткость пружины).

Знак «-» показывает, что сила всегда направлена в сторону положения равновесия.

Согласно второго закона Ньютона (произведение массы тела на ускорение равно сумме всех действующих сил), получаем:

, делим уравнение наm

Заменяя , получим

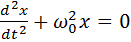- дифференциальное уравнение незатухающего гармонического колебания.

Решением данного уравнения является функция:

(1) - уравнение смещения

где, – амплитуда колебаний,

- фаза колебаний

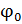– начальная фаза (при )

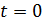– круговая частота колебаний ().

Тогда частота колебаний:

Период колебаний находим из формулы:

или

График функции (1) имеет вид:

Определим скорость и ускорение незатухающего колебания:

где - это максимальная скорость (или амплитуда скорости)

Затухающие колебания

Если в системе кроме упругой силы действует сила трения

где – коэффициент трения (характеризует свойства среды оказывать сопротивление).

Тогда второй закон Ньютона принимает вид:

или

делаем замену , тогда

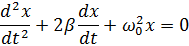
получилидифференциальное уравнение затухающего колебания.

где, 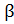– коэффициент затухания

- круговая частота собственных колебаний системы (без затухания).

Решение дифференциального уравнения существенно зависит от знака разности:

где, - круговая частота затухающих колебаний.

Если , тогда решением уравнения будет функция:

- уравнение смещения.

Представим график этой функции:

Период затухающих колебаний:

Коэффициент затухания характеризует быстроту убывания амплитуды колебаний. Чем больше , тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда.

На практике степень затухания определяется через логарифмический декремент затухания – это величина, равная натуральному логарифму отношения двух последовательных амплитуд колебаний, разделенных интервалом времени, равным периоду колебаний: