Предположим, что проводится испытание, заключающееся в бросании правильно выполненного игрального кубика два раза подряд. Возможные результаты такого испытания представим в виде таблицы:
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
| 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
| 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
| 6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
В каждой ячейке таблицы первая цифра – результат первого бросания, вторая цифра – результат второго бросания.
Как видно из таблицы, возможны 36 вариантов исхода двукратного бросания кубика. Попробуем рассчитать вероятность выпадения два раза подряд числа 6. Для правильно выполненного кубика все приведенные в таблице исходы равновероятны и, следовательно, выпадение двух шестерок, как и выпадение любой другой пары одинаковых чисел, имеет вероятность, равную  . Но
. Но 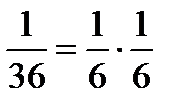 , то есть вероятность выпадения подряд двух шестерок равна произведению вероятности выпадения числа 6 на самое себя. Данный пример иллюстрирует теорему умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей.
, то есть вероятность выпадения подряд двух шестерок равна произведению вероятности выпадения числа 6 на самое себя. Данный пример иллюстрирует теорему умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей.
Для случая двух независимых событий  и
и  :
:
 .
.
Так как события 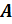 и
и  независимы, то каждому из
независимы, то каждому из  случаев, благоприятствующих событию
случаев, благоприятствующих событию 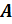 , соответствуют
, соответствуют  случаев, благоприятствующих событию
случаев, благоприятствующих событию  . Таким образом, общее число случаев, благоприятствующих появлению событий
. Таким образом, общее число случаев, благоприятствующих появлению событий 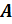 и
и  , равно
, равно  , а общее число равновозможных событий равно
, а общее число равновозможных событий равно  , где
, где  и
и  – числа равновозможных событий соответственно для
– числа равновозможных событий соответственно для 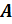 и
и  . Отсюда вероятность совместного появления событий равна:
. Отсюда вероятность совместного появления событий равна:

Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых событий.
Вероятность наступления в некотором испытании одновременно двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое события имело место:
 – формула Байеса
– формула Байеса
При решении задач необходимо:
1. Выяснить, являются ли эти события независимыми или зависимыми
2. Определить вероятности каждого отдельного события
3. Определить вероятность одновременного наступления этих событий
Задача: Считая, что рождение девочки или мальчика – это независимые и равновозможные события. Определить появление в семье подряд трех девочек.
Дано: Решение
 Согласно теореме умножения вероятностей для
Согласно теореме умножения вероятностей для
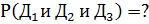 независимых событий:
независимых событий:

Задача: В коробке находится 10 красных и 20 синих карандашей. Определить вероятность внимания двух красных карандашей подряд.
Дано: Решение

|
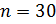 Вероятность вынимания первого красного карандаша:
Вероятность вынимания первого красного карандаша:



|
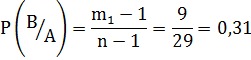
Тогда, согласно теореме умножения вероятностей для зависимых событий, вероятность вынимания двух красных карандашей подряд будет:

Задача: На обследование прибыла группа из 10 человек. Трое из них больны. Врач приглашает в кабинет по 2 человека. Найти вероятность того, что:
а) оба больны
б) оба здоровы
в) один болен и один здоров.
Решение:
а) обозначим события:  – первый из вошедших к врачу – болен,
– первый из вошедших к врачу – болен,  – второй – болен. События
– второй – болен. События  и
и  зависимые.
зависимые.

б) обозначим события:  – первый здоров;
– первый здоров;  – второй здоров. События зависимые
– второй здоров. События зависимые

в) ситуация 1
 – первый здоров;
– первый здоров;  – второй болен
– второй болен

ситуация 2
 - первый болен;
- первый болен;  – второй здоров
– второй здоров

т.к. обе ситуации подходят, то:
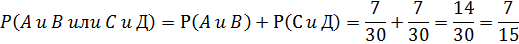
Задача. Из 20 ампул с лекарственными препаратами ёмкостью по 2 мл, в 5 ампулах количество препарата отличалось от нормы. Какова вероятность, что из трёх наугад взятых ампул хотя бы одна окажется нестандартной?
Дано: Решение
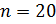 Задача решается от противного. Противоположными будут
Задача решается от противного. Противоположными будут
 события, что во всех трёх ампулах лекарственного
события, что во всех трёх ампулах лекарственного
 препарата содержится в норме (2мл).
препарата содержится в норме (2мл).
Вероятность, что в первой ампуле содержится норма препарата:

во второй:

в третьей:

Вероятность, что во всех трёх ампулах содержится норма лекараственного препарата:

Сумма вероятностей противоположных событий равна единице
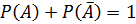

Ответ: 
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
| ПЛАН: | 6.1. Случайные величины. Закон распределения дискретных случайных величин. Функция распределения непрерывных случайных величин. |
| 6.2. Числовые характеристики случайных величин. | |
| 6.3. Нормальный закон распределения случайных величин. |
В медико-биологических исследованиях огромную роль играет нормальный закон распределения (закон Гаусса). При действии большого числа случайных факторов, каждый из которых сам по себе оказывает независимо от других незначительное действие на случайную величину, последняя подчиняется закону Гаусса. Так, например, закону Гаусса подчиняются: рост и вес людей; артериальное давление крови, длина сосудов, размеры органов, вес и объем мозга, содержание ферментов у людей и др.




