При достаточно большом объеме выборки можно сделать вполне надёжные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема 
. Кроме того, почти всегда оказывается неизвестной генеральная дисперсия.
Имея выборку, можно найти лишь исправленную выборочную дисперсию 
и выборочную среднюю 
. Выразим отклонение выборочного среднего от генерального через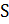 
и некоторый параметр 
.
или 
Или представим это в виде интервала:
где - коэффициент Стьюдента, который находится по таблицам, согласно заданному объему выборки и доверительной вероятности.
Задача 1. Содержание свободного гепарина крови принимало следующие значения 
с частотой появления 
.
| (мг,%)
| 5,7 | 5,9 | 6,3 | 5,6 | 4,1 | 4,0 | 4,5 | 5,0 | 5,1 | 6,7 |
|
| 5 | 11 | 2 | 7 | 4 | 15 | 13 | 23 | 9 | 1 |
Вычислить выборочную среднюю арифметическую, медиану и моду. Построить полигон частот.
Решение:
Выборочная средняя определяется по формуле:
где, 
Для определения медианы по заданным параметрам 
строим вариационный ряд:
|
| 4,0 | 4,1 | 4,5 | 5,0 | 5,1 | 5,6 | 5,7 | 5,9 | 6,3 | 6,7 |
|
| 15 | 4 | 13 | 23 | 9 | 7 | 5 | 11 | 2 | 1 |
При четном числе вариант медиана определится как среднее арифметическое из двух центральных вариант:
Мода:
Используя данные таблицы, строим полигон частот:
Задача2. Измерения роста мужчин представлены статистическим интервальным рядом распределения:
|
(см)
| 150-154 | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 | 182-186 |
|
| 1 | 3 | 11 | 23 | 25 | 22 | 11 | 3 | 1 |
Построить гистограмму. Вычислить выборочное среднее арифметическое, медиану и моду.
Решение:
Находим шаг интервала 
:
Заполняем таблицу:
|
(см)
| 150-154 | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 | 182-186 |
|
| 1 | 3 | 11 | 23 | 25 | 22 | 11 | 3 | 1 |
(см)
| 154 | 156 | 160 | 164 | 168 | 172 | 176 | 180 | 184 |
(см)
| 152 | 468 | 1760 | 3772 | 4200 | 3784 | 1936 | 540 | 184 |
| 0,25 | 0,75 | 2,75 | 5,75 | 6,25 | 5,5 | 2,75 | 0,75 | 0,25 |
Выборочное среднее арифметическое
Медиана:
Мода:
Задача 3. Найти исправленную дисперсию ,стандарт отклонения 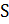для показателя гемоглобина, значения которого приведены ниже.
| Показатель гемоглобина
| 73 | 72 | 71 | 70 | 69 | 68 | 67 | 66 | 65 | |
| Число лиц
| 2 | 4 | 6 | 10 | 11 | 7 | 5 | 4 | 1 | n=50 |
Решение:
Составим дополнительную таблицу:
| 146 | 288 | 426 | 700 | 759 | 476 | 335 | 264 | 65 | 
|
| 14,59 | 7,95 | 3,3 | 0,67 | 0,32 | 1,39 | 4,75 | 10,11 | 17,47 | |
| 29,18 | 31,8 | 19,8 | 6,72 | 3,56 | 9,74 | 23,73 | 40,44 | 17,47 | 
|
Находим выборочное среднее арифметическое по формуле:
Находим исправленную дисперсию по формуле:
Стандарт отклонения
Задача 4. Найти исправленную дисперсию стандарт отклонения 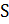для веса щитовидной железы, значения которого даны в таблице:
| ( г )
| 60 | 68 | 70 | 72 | 90 | 100 | 105 | 120 | 125 | 130 |
|
| 2 | 2 | 6 | 5 | 7 | 8 | 7 | 2 | 3 | 4 |
Решение:
Для удобства решения задачи заполним таблицу:
|
| 60 | 68 | 70 | 72 | 90 | 100 | 105 | 120 | 125 | 130 |
|
| 2 | 2 | 6 | 5 | 7 | 8 | 7 | 2 | 3 | 4 |
|
| 120 | 136 | 420 | 360 | 630 | 800 | 735 | 240 | 375 | 520 |
|
| 1156 | 676 | 576 | 484 | 16 | 36 | 121 | 676 | 961 | 1296 |
|
| 2312 | 1352 | 3456 | 2420 | 112 | 288 | 847 | 1352 | 2883 | 5184 |
Рассчитаем суммы:
Исправленную дисперсию определяем по формуле:
где - частота появления варианты
- значение варианты
-сренее выборочное арифметическое
-объем выборки.
Используя данные таблицы, находим:
Стандарт отклонения (исправленное среднее квадратическое отклонение) находим по формуле:
(г)
Ответ: 
(г)
Задача 5. Пять измерений относительной вязкости крови человека дали следующие результаты: 4,80; 4,70; 4,85; 4,75; 4,90 (10-3 Па∙с). Найти среднее арифметическое и величину доверительного интервала при доверительной вероятности 0,95.
Решение:
1. Определим среднее арифметическое
Определим стандарт отклонения среднего арифметического:
для этого составим таблицу:
|
| 4,80 | 4,70 | 4,85 | 4,75 | 4,90 | |
| 0 | -0,1 | 0,05 | -0,05 | 0,1 | |
|
| 0 | 0,01 | 0,0025 | 0,0025 | 0,01 | 
|
Определим доверительной интервал при доверительной вероятности 
. По таблице находим коэффициент Стьюдента, 
.
Зная, что доверительной интервал определяется следующим образом:
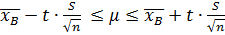находим
Таким образом, истинное значения относительной вязкости крови человека, с вероятностью 95%, лежит в интервале от 4,72∙10-3 Па∙с до 4,87∙10-3 Па∙с.
ТЕОРИЯ КОРРЕЛЯЦИИ
| ПЛАН: | 8.1. Функциональная, статистическая и корреляционная зависимости. |
| 8.2. Корреляционное поле. Линии и уравнения регрессии. | |
| 8.3. Коэффициент корреляции и его свойства. | |
| 8.4. Экспериментальное определение коэффициента корреляции для линейной зависимости. |
Выявление связей (корреляций) между различными случайными параметрами и случайными процессами широко используется в медицинской диагностике. С помощью корреляционного анализа решаются задачи установления обоснованного диагноза. Целью диагноза является установление с высокой надежностью вида заболевания при определенных симптомах. Установление корреляций между различными показателями состояния больного и влиянием их изменений на жизнедеятельность организма является важной задачей лабораторных и клинических исследований. Все системы, ткани, органы, клетки организма находятся в корреляционной связи друг с другом.
Определение коэффициента корреляции позволяетсяопределить существование и степень связи между различными выборками.
