Пусть функция 
задана графически (рис. 1). Возьмем на кривой произвольно точку 
. Зададим приращение аргументу 
, тогда функция получит приращение 
и на графике мы получим точку 
с координатами 
. Проведем секущую 
и обозначим угол наклона секущей к оси 
через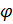 
:
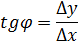
Пусть 
, тогда точка будет стремиться к точке 
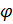, величина угла будет изменяться. При приближении к касательной 
, угол 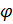приближается к углу 
, следовательно, 
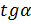равен угловому коэффициенту касательной:
Рис.1 Геометрический смысл производной.
Таким образом, геометрический смысл производной заключается в том, что она есть угловой коэффициент касательной к графику функции в этой точке.
ОСНОВНЫЕ СВОЙСТВА ПРОИЗВОДНЫХ
1. Производная постоянной величины равна нулю:
где, 
2. Производная аргумента по самому аргументу равна единице:
.
3. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций:
Например: 
.
4. Производная произведения двух функций определяются по формуле:
Например: 
.
5. Производная частного двух функций определяются по формуле:
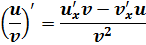
Например:
ТАБЛИЦА ПРОИЗВОДНЫХ ОТ ОСНОВНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. 
2. 
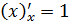
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
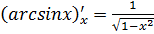
13. 
14. 
15. 
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть у нас есть сложная функция: 
. Эту сложную функцию (или функцию от функции) можно представить в виде элементарных функций, которые являются её промежуточными аргументами.
Если функция 
имеет производную 
, а функция 
производную 
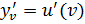в соответствующей точке 
, то сложная функция в данной точке 
имеет производную 
, которая находится по формуле:
Например:
1. 
2. 
3. 
4. Определить зависимость градиента концентрации от координаты, если зависимость концентрации от координаты задана функцией: 
, где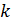 
- константа, 
- концентрация вещества при 
.
Решение: Величина градиента концентрации определяется выражением 
и характеризует быстроту изменения концентрации при изменении координаты. Пользуясь правилом дифференцирования сложной функции получим:
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Производная от производной первого порядка называется производной второго порядка и обозначается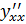 
или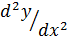 
.
Производная от производной второго порядка называется производной третьего порядка и т.д.
Физический смысл производной второго порядка заключается в том, что вторая производная от пути 
по времени 
равна мгновенному ускорению переменного движения:
Например:
1. Найти производную второго порядка от функции: 
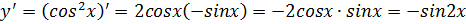
2. Найти скорость и ускорение точки, совершающей гармонические колебания по закону:
ДИФФЕРЕНЦИАЛ ФУНКЦИИ И
ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Дифференциалом функции называется произведение производной этой функции на дифференциал аргумента:
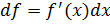
Для объяснения геометрического смысла дифференциала функции обратимся к рисунку 1. Из треугольника 
находим:
.
Но из определения дифференциала функции: 
, следовательно
.
Таким образом, отрезок 
, равный дифференциалу функции геометрически представляет собой приращение ординаты касательной к графику функции в точке с абсциссой 
при переходе от точки касания в точку с абсциссой 
.
Например:
Найти дифференциал функции: 
.
