Ограниченные и монотонные функции

Среди важнейших классов функций можно указать ограниченные и монотонные функции.

Заметим, что хотя по самой своей сути график функции отличается наглядностью, на рисунке умещается лишь часть графика функции. Поясним сказанное на примерах (рис. 3 а, б, в, г).

                   а)                                                   б)

                   в)                                                   г)

Рис. 3

Полностью график изображен лишь в случае а), в случаях б) и в) областью определения является бесконечный промежуток поэтому, естественно, на рисунках уместилась только часть графика функции. В случае г) область определения – промежуток конечной длины – [1, 3], однако в этом случае уместилась только часть графика функции.

В случаях б), в), г) заданы так называемые неограниченные функции.

Определение. Функцию у = f (х)называют ограниченной на промежутке D, если можно указать такие два числа А и В, что для всех х Î D выполняются неравенства: А < f (х) < В.

В противном случае функцию называют неограниченной (на рассматриваемом промежутке).

Заметим, что на бесконечных промежутках могут быть определены как ограниченные, так и неограниченные функции. Примеры ограниченных функций: у = sin х, у = соs х. Примерами неограниченных функций могут быть, в частности, функции, изображенные графически на рис. 3в случаях  б), в).

На промежутках конечной длины также могут быть определены как ограниченные, так и неограниченные функции. Такие примеры также имеются на рис. 3: в случае а) функция ограниченная, в случае г) функция неограниченная.

Возникает вопрос: связаны ли взаимно понятия ограниченность (неограниченность) функции и конечность промежутка, на котором она определена? Для ответа на этот вопрос укажем вначале еще на один из важнейших классов функций: монотонные функции.

Определение. Функцию у = f (х)называют неубывающей на промежутке D, если для любых х ₁и х ₂из этого промежутка, удовлетворяющих неравенству х ₁< х₂, выполняется неравенство f (х ₁) £ f (х ₂).Если же вместо последнего неравенства имеет место неравенство f (х ₁) ³ f (х ₂), то говорят о невозрастающей функции.

Функция называется монотонной, если она либо невозрастающая, либо неубывающая.

Теперь можно сформулировать ответ на поставленный выше вопрос в виде следующей теоремы.

Теорема. Если функция определенная на замкнутом промежутке монотонная, то она ограниченная.

Доказательство. Пусть функция у = f (х)определена на замкнутом промежутке [ а; в ].Обозначим :f (а) = А, f (в) = В. Предположим для конкретности, что рассматривается неубывающая функция. В этом случае имеем А £ В. Выберем произвольную точку х из отрезка [ а; в ]. Поскольку а < х, то, согласно условию теоремы А < f (х).Поскольку х < в, то f (х) < В. Таким образом, для всех x из области определения функции выполняются неравенства А £ f (х) £ В. Теорема доказана.

Замечание. Если в определенной монотонной функции в неравенстве f (х ₁) £ f (х ₂) или f (х ₁) ³ f (х ₂) убрать знак равенства, то получим так называемую строго монотонную функцию: либо возрастающую, либо убывающую.

Для строго монотонной функции существует обратная функция.

Сложная функция

Далее перейдем к понятию «сложная функция». Возьмем в качестве примера функцию 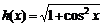. Будем рассматривать также функции и 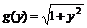. Итак, обратимся к трем указанным функциям: h (x), f (x), g (у) (здесь целесообразно немного упростить символику).

Функция h (x) есть сложная функция, составленная из функций f (x) и g (y): h (x) = g (f (x)). Функция  определена на промежутке , она является отображением f промежутка  на промежуток [–1; 1]. Функция 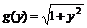 есть отображение g промежутка [–1; 1] на промежуток 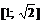. Наконец, функция 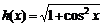, определенная на промежутке  есть отображение h этого промежутка на промежуток .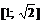

Отображение h есть результат последовательного осуществления отображений f и g. В таких случаях говорят о композиции отображений и применяют запись h = g ° f (правую часть равенства надо читать справа налево: сначала используется отображение f, а затем отображение g).

Итак, если задана функция у = f (x) с областью определения D и областью значений F, которая содержится в области определения другой функции h = g (y), тогда имеет смысл функция h (x) = g (f (x)) с областью определения D, которая называется сложной функцией от х.