Простейшие преобразования графиков функций

График функции обычно строят по точкам, т.е. сначала строят несколько точек принадлежащих графику (все точки графика построить вообще нельзя, потому что их может оказаться бесконечное множество), а затем эти точки соединяют плавной линией с учетом простейших свойств данной функции. Заметим, что график функции может состоять из конечного или бесконечного множества отдельных изолированных точек, в этом случае отпадает необходимость соединять их линией. Не следует думать, что можно построить график любой функции. Например, график функции Дирихле:

построить нельзя, его можно образно только представить себе, состоящим из множества точек, расположенных на оси Ox и имеющих иррациональные абсциссы, и множества точек, расположенных на прямой y = 1 (прямая, параллельная оси Ох, проведенная выше этой оси на одну единицу), имеющих рациональные абсциссы. Из определения функции видно, что она задана на всей числовой прямой, т.е. в интервале (–¥, +¥), а область изменения функции состоит из двух точек 0 и 1. Найдем несколько значений этой функции:

D (2) = 1; D (0) = 1; D () = 0; D (2) = 1; D (p) = 0.

График функции у = x², заданной на множестве рациональных чисел, также построить нельзя.

График функции у = п ², заданной на множестве натуральных чисел, будет состоять из бесконечного множества отдельных изолированных точек (рис. 4).

График функции f (x) = sign x = (читается «сигнум икс». По латыни signum означает «знак») состоит из двух ветвей и одной точки (рис. 5).

Эта функция задана на всей числовой прямой, т.е. в интервале (–¥, +¥), а множество ее значений состоит из трёх точек: –1, 0 и 1.

Иногда, зная график какой-нибудь функции, можно путем некоторого геометрического преобразования получить график другой функции.

Рассмотрим следующие преобразования графика функции:

1) осевая симметрия относительно оси абсцисс;

2) осевая симметрия относительно оси ординат;

3) параллельный перенос в направлении оси абсцисс;

4) параллельный перенос в направлении оси ординат;

5) растяжение (сжатие) по направлению оси абсцисс;

6) растяжение (сжатие) по направлению оси ординат.

Свойства этих преобразований состоят в том, что точка (х, у) плоскости переходит: при первом преобразовании в точку (х, – у), при втором – в точку (– х, у); при третьем – в точку (х + а, у), где а ³ 0; при четвертом – в точку (х, у + b), где b ³ 0, при пятом – в точку (kх, у), где k > 0, при шестом – в точку (х, mу), где m >0.

Перечисленные свойства преобразований можно принять за определения преобразований.

Пусть известен график функции y = f (x). Соответственно перечисленным преобразованиям из него могут быть получены графики функций: y = – f (x); y = f (– x); y = f (x ± а); y = f (x) + b; y = f (kx); y = mf (x).

В следующих далее параграфах 4-9 изложено доказательство этих утверждений.

В параграфах 10, 11 излагается способ построения графика функций в случае, если требуется последовательное выполнение нескольких геометрических преобразований графика.

Обратная функция

Пусть функция y = f (x) (1)

задана в сегменте [ а, b ], а множество ее значений (область изменения функции) есть сегмент [ с; d ].

Если каждому значению у из сегмента [ с; d ] соответствует одно значение х из сегмента [ а, b ], для которого f (х) = у, то в сегменте [ с; d ] можно определить функцию

x = j (y) (2)

так, что каждому значению у, взятому в сегменте [ с, d ], будет соответствовать одно значение х из сегмента [ а, b ], для которого f (х) = у. Функция (2) называется обратной по отношению к данной функции (1), удовлетворяющей для всех значений у, взятых в сегменте [ с, d ], условию у = f (j (y)). Заметим, что если функция (2) обратная по отношению к функции (1), то, очевидно, что функция (1) обратная по отношению к функции (2).

Функции (1) и (2) называют взаимно обратными. Заметим также, что в определении вместо сегментов [ а, b ] и [ с, d ] можно взять любые промежутки, например, интервалы (а, b) и (с, d).

Имеет место теорема, выражающая достаточное условие существования обратной функции.

Теорема. Если функция у = f (x) строго монотонна, то разные х отображаются в разные у.

Докажите эту теорему самостоятельно.

Заметим, что график прямой функции у = f (х),заданной в сегменте [ а, b ] (с £ у £ d), и обратной функции х = j (у), заданной в сегменте [ с, d ] (a £ x £ b), будет один и тот же (рис. 6). Следовательно, для построения графика функции у = f (х), заданной в промежутке [ а, b ] (с £ у £ d), можно построить график обратной функции х = (у), заданной в промежутке [ с, d ](а £ х £ b). Если же в обратной функции х = j (у) независимую переменную обозначить через х, а функцию через у, то областью определения обратной функции х = j (у) будет промежуток [с, d ] на оси Ох (вертикальной), а областью изменения функции промежуток [ а, b ] на оси Оу (горизонтальной), т.е. произойдет перемена названий осей координат. Чтобы придать обычное общепринятое расположение осям координат, надо повернуть плоскость чертежа хОу на 180° вокруг биссектрисы первого и третьего координатных углов, при этом и график обратной функции будет получен как зеркальное отражение графика прямой функции y = f (x) относительно этой биссектрисы (рис. 7).

На практике переход от исходной функции к обратной очень просто выполняется графически.

График обратной функции симметричен по отношению к графику исходной функции, причем осью симметрии служит прямая у = х.

Это хорошо видно на рис. 8 (а, б).

а) б)

Рис. 8

На рисунке 8 а) исходная функция обратная ей функция .

На рисунке 8 б) исходная функция обратная ей функция .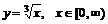

П р и м е р ы. Найти функции, обратные к данным и указать их области определения.

1) y = 2 x – 3; 2) y =

Решение.

1) Функция у = 2 х – 3 определена в интервале (–¥, +¥), множество ее значений также есть интервал (–¥, +¥), причем эта функция строго возрастающая (докажите!), следовательно, по достаточному условию существования обратной функции, определяется в этом интервале обратная функция.

Сначала выразим в заданной формуле х через у: х = .

Поменяем обозначения х и у местами в последней формуле, получим у = . Это и есть функция, обратная к функции y = 2 x – 3.

2) Функция y = задана в интервалах (–¥, 0) и (0, +¥), убывает в этих интервалах (докажите!). Множество значений этой функции также интервалы (–¥, 0) и (0, +¥), следовательно, существует в этих интервалах обратная однозначная убывающая функция х = . Поменяв обозначения х и у местами, получаем y = . Нетрудно заметить, что данная функция y = совпадает со своей обратной.