Определение. Если каждому числу х, взятому из множества X, по некоторому правилу или закону ставится в соответствие единственное число у, то говорят, что задана функция, которая обозначается y = f (x).
Числовое множество Х называют областью определения функции, а множество значений Y называют областью изменения функции.
Из приведенного определения следует, что функция считается заданной, если: 1) известна область определения функции и 2) указано правило или закон, по которому каждому значению х ставится в соответствие одно определенное значение у, короче – известен закон соответствия. Обычно областью определения числовой функции являются замкнутый промежуток, или сегмент [ а, в ]: а £ х £ в, открытый промежуток, или интервал (а, в): а < х < в, полуоткрытые промежутки, или полуинтервалы [ а, в), (а, в ]: а £ х < в, а < x £ в. К ним присоединяются: (а, +¥), (–¥, а), [ a, +¥), (–¥, a ], (–¥, +¥).
Область определения функции может состоять из одного или нескольких промежутков и из отдельных точек числовой прямой.
Чтобы показать, что у есть функция от переменной х, пользуются обозначениями:
у = f(х), у = j (х), у = А (х), у = у (х) и т. д. Функцию можно обозначить любой буквой.
Запись y =f (х) [ а, в ] будем понимать так: функция f (х) определена (задана) в указанном промежутке.
Чтобы найти значение у по данному значению х, взятому из промежутка [ а, в ], надо произвести над ним некоторую определенную систему операций f. Отсюда следует, что если функция задана, т.е. известно множество значений х и закон соответствия f, то определено и множество значений у.
На рисунке 1 показана область определения функции у = f (x) – промежуток [ а. b ] и область изменения – промежуток [ с, d ], или, что одно и то же, аргумент x данной функции изменяется от а до в (a £ x £ в), а функция y изменяется от с до d (c £ y £ d).
Может оказаться, что область изменения функции состоит из одного какого-нибудь числа с, или, иначе говоря, каждому значению х, взятому из области определения функции, соответствует единственное число с. В этом случае функция постоянна и записывается так:
f (x)= c (рис. 2), или f (x) = const.
Частное значение функции f (x) в точке x 0 обозначается f (x 0). Например, если f (x)= x 3 – 5 x + 3, то f (2) = 23 – 5 × 2 + 3 = 1, f (0) = 3; если j (t) =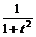 
, то j (0) = 1, j (3) = 0,1, j (a) = 
и т.п.
На рис. 1 изображено частное значение функции в точке x 0 равное y 0.
Среди основных элементарных функций есть функции вида f (x) = р (x), где р (x) – многочлен, их называют целыми рациональными функциями. А так же функции вида 
, где р (x) и q (x) – многочлены, их называют дробно-рациональными функциями. Частное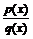 
определено, если q (x) не обращается в нуль. Поэтому область определения дробно-рациональной функции – множество всех действительных чисел, из которого исключены корни многочлена q (x).
В этой главе мы будем рассматривать свойства и графики целых рациональных и дробно-рациональных функций.
Способы задания функции
1. Аналитический способ задания функции.
Если функция y = f (х) задана одной или несколькими формулами на различных промежутках изменения аргумента х, то говорят, что функция задана а н а л и т и ч е с к и м способом.
При таком задании функции прямо указывается, какие действия и в каком порядке надо произвести над значением х и постоянными числами, чтобы получить соответствующее значение у.
П р и м е р ы.
1) у = х3 + 5.
Чтобы получить значение у, надо возвести значение х в третью степень и к полученному результату прибавить 5.
2) 
.
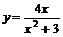В этом примере, чтобы найти значение у, надо произвести над значением х и постоянными числами четыре действия (умножение, возведение в степень, сложение и деление).
3) y = lg(x 2 + 5 x – 2).
Значение данной функции находится при помощи пяти действий.
Если функция задана аналитически у = f (х) и область определения этой функции не указана, то под последней понимают множество действительных значений х, при которых функция f (х) принимает также действительные значения.
П р и м е р ы известных нам функций.
Площадь круга вычисляется по формуле S = p r 2, где r – радиус круга, отсюда площадь круга есть функция от радиуса r, т.е. S = f (r) = p r 2 (r > 0).
Площадь квадрата вычисляется по формуле S = х2, где х — длина стороны квадрата. Следовательно, площадь квадрата есть функция от длины его стороны. Эту зависимость можно записать так:
S (x) = x 2 (x > 0).
Объём шара V = 
p r3 (r > 0), где r – радиус шара. Следовательно, объем шара есть функция от его радиуса, т.е.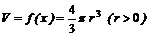 
.
Однако не каждую функцию можно задать аналитически, например, температура воздуха в течение суток изменяется, т.е. температура воздуха Т является функцией от времени t: T = j (t)
Здесь аргументом функции будет время. Значения температуры воздуха получаем путем измерения (наблюдения) лишь для некоторых значений аргумента t, и закон изменения температуры в зависимости от времени еще не может быть выражен какой-либо формулой.
2. Табличный способ.
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие значения функции.
Читатель неоднократно пользовался таблицами тригонометрических функций, логарифмическими и другими таблицами. (Вспомните «Четырехзначные математические таблицы» В.М. Брадиса). Приведенную выше функцию T = j (t)можно задать с помощью таблицы. Будем, например, измерять температуру воздуха в течение суток, начиная с нуля часов с интервалами в один час, получим таблицу, состоящую из 25 значений аргумента t (t = 0, 1, 2, 3,..., 24) и 25 значений функции Т. Первое множество будет областью определения функции, а второе – областью изменения функции. В практической деятельности очень часто приходится пользоваться табличным способом задания функции. Этот способ дает возможность для указанных в таблице значений аргумента получать без вычислений соответствующие значения функции. С другой стороны, он имеет существенный недостаток. В таблице мы не можем найти те значения функции, которые соответствуют значениям аргумента, не содержащимся в таблице, в то время как при аналитическом способе, вообще говоря, мы можем вычислить значение функции при любом значении аргумента, принадлежащем области определения функции.
3. Графический способ.
Графиком функции у = f (х) называют множество точек плоскости, прямоугольные координаты х и у которых удовлетворяют уравнению у = f (x).
Функцию у = f (х)называют заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно.
Функциональная зависимость предполагает, что каждому значению х из области определения функции соответствует одно, и только одно, значение у. Это означает, что любой перпендикуляр, восстановленный к оси абсцисс в какой-либо точке из области определения функции, пересекает ее график лишь в одной точке.
Построение графика и нахождение на нем значений функции сопряжено с погрешностями.
Зависимость между временем и температурой воздуха, упомянутую выше, можно задать и с помощью графика, воспользовавшись, например, самопишущим прибором термографом.
Заметим, что в математике почти всегда прибегают к графической иллюстрации функции, благодаря этому достигается наглядность свойств данной функции, что значительно облегчает ее исследование. Это является достоинством графического способа задания функции.
Выше мы уже воспользовались этим способом, изобразив графики некоторых функций. В дальнейшем при изучении функций наряду с аналитическим способом задания функций будем пользоваться и геометрической интерпретацией.
Мы рассмотрели три способа задания функции: аналитический, табличный и графический. Из этих трёх способов основным является аналитический. Приведем пример, когда функция определяется способом, не упомянутым выше.
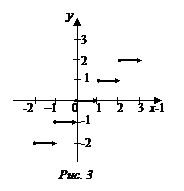4. Словесное описание функции.
Пусть у означает наибольшее целое число, не превосходящее числа x, или как иногда говорят короче, «целую часть числа x». Из свойств этой функции следует, что область её определения есть всё множество действительных чисел и известен закон соответствия. Таким образом, функция y задана на множестве действительных чисел при помощи словесного описания закона соответствия (рис. 3).
Целую часть числа х принято обозначать символом [ х ] или Е [ х ].Следовательно, можно написать:
у = [ х ] или у = Е (х).
Область изменения функции состоит из множества целых чисел. Найдем несколько частных значений этой функции:
[0, 5] = 0; [2, 3] = 2; [ 
] = 1; [–1, 3] = –2; [ p ] = 3; [– p ] = –4.
Заметим, что каждый способ задания функции имеет свои достоинства.
Формулы часто используют потому, что с ними удобно производить вычисления, их можно преобразовывать и анализировать, выясняя свойства функции. Табличный способ предпочитают тогда, когда трудно вычислить значения функции или когда она может принимать, лишь несколько отдельных значений. Словесный – наиболее прост и доходчив, если, конечно, функцию удается описать простыми фразами.
Графический способ представления функции – самый наглядный. График функции – это линия (или множество отдельных точек), дающая цельное представление о характере изменения функции по мере изменения ее аргумента. Благодаря своей наглядности графический способ задания функций часто сопутствует другим способам. Выведя формулу какой-либо функциональной зависимости, исследователь вслед за этим строит еще ее график. Многие компьютеры имеют графический редактор. Графики большинства функций имеют названия. График линейной функции – прямая, график квадратичной функции – парабола, график обратно-пропорциональной зависимости – гипербола и так далее.
