ВАРИАНТ 1
1. Если а и b – различные действительные числа (а < b), то числовое множество  обозначается в виде:
обозначается в виде:
1) [ a,b ]; 2){ a,b }; 3) (a,b); 4) (-¥,+ ¥).
2. Множество, состоящее из всех элементов, принадлежащих и множеству А и множеству В одновременно, называется:
1) пересечением множеств А и В и обозначается А Ç В;
2) объединением множеств А и В и обозначается А È В;
3) разностью множеств А и В и обозначается А \ В;
4) декартовым произведением двух множеств А и В и обозначается А ´ В.
3. Укажите множество А = В \ С, которое является разностью множеств В ={10, 12, 16, 19, 21} и С ={10, 16, 21}:
1) А={10, 12, 16, 19, 21}; 3) А={10, 16, 21};
2) А={12, 19}; 4) А=Æ.
4. Запишите для множеств А, В и С свойство ассоциативности пересечения.
5. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. Постройте круги Эйлера для данных множеств и отметьте штриховкой область, изображающую множество  .
.
6. У кажите характеристическое свойство элементов множества Y=K Ç L \  ,
,
если K ={ x/ x Î R, x <4}, L ={ x/ x Î R, -5< x <40}, M ={ x/ x Î R, x ³ 0}.
7. Из 80 школьников 40 играют в футбол, а 50 – в волейбол. Каким может быть число школьников, играющих в обе игры? Хотя бы в одну из игр?
8. Проиллюстрируйте на кругах Эйлера, что для любых множеств А и В верно равенство: (А \ В)È(А Ç В)= А.
9. Изобразите на координатной плоскости А ´ В, если А =(-3;3], В =(1;3).
10. Правило суммы в комбинаторике для двух непересекающихся множеств формулируется как:
1) n (А È В)= n (A)· n (B);
2) n (А È В)= n (A)+ n (B)- n (А Ç В);
3) n (А È В)= n (A) n (B)- n (А È В);
4) n (А È В)= n (A)+ n (B);
11. m! обозначает:
1) произведение всех целых чисел;
2) произведение всех натуральных чисел от 1 до m;
3) сумму всех натуральных чисел от 0 до m;
4) произведение всех неотрицательных целых чисел.
12. Упорядоченные k -элементные множества, составленные из элементов m -элементного множества X, называются:
1) размещениями с повторениями;
2) сочетаниями без повторений;
3) перестановками без повторений;
4) размещениями без повторений.
13. На тарелке лежат 5 яблок и 4 груши. Сколькими способами можно выбрать один плод?
1) 14 способами; 3) 5 способами;
2) 20 способами; 4) 4 способами.
14. Сочетания без повторений из m по k вычисляются по формуле:
1) m × k; 2) mk; 3) 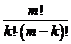 ; 4)
; 4)  .
.
15. Сколькими способами из 10 человек можно выбрать комиссию, состоящую из 3 человек?
16. Найдите значение выражения:  .
.
17. Вычислите:  .
.
18. Сколько пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4 при условии, что каждая цифра входит в пятизначное число только один раз?
19. Перечислите свойства, входящие в содержание понятия «прямоугольник».
20. Высказывание «если А, то В» называется:
1) конъюнкцией высказываний А и В;
2) дизъюнкцией высказываний А и В;
3) импликацией высказываний А и В;
4) эквиваленцией высказываний А и В.
21. Дизъюнкция двух высказываний А и В ложна тогда и только тогда, когда:
1) А – «И», В – «Л»; 3) А – «И», В – «И»;
2) А – «Л», В – «И»; 4) А – «Л», В – «Л».
22. Сформулируйте правило заключения и приведите пример умозаключения, которое построено по этому правилу.
23. Составьте таблицу истинности для высказывания: (ĀÚВ)ÞС.
24. Даны предикаты A (x): «x > 3» и B (x): «x < 4». Найдите множество истинности Т АÙВ предиката А (x)Ù В (x).
25. Между элементами множеств Х =(1, 2, 3, 4, 5) и Y =(1, 4, 6) задано соответствие Р – «х < y», причем х Î Х, y Î Y. Постройте график соответствия Р.
26. Если отношение R на множестве X транзитивно и антисимметрично, то R является отношением:
1) строгого порядка; 3) нестрогого порядка;
2) эквивалентности; 4) биективным.
27. Докажите, что множество натуральных чисел равномощно множеству нечетных натуральных чисел.
28. Является ли отношение «больше», заданное на множестве натуральных чисел, отношением эквивалентности?
29. В каком случае классификация выполнена верно:
1) множество всех треугольников можно разбить на остроугольные, тупоугольные и прямоугольные;
2) множество всех треугольников можно разбить на классы равнобедренных, равносторонних и разносторонних треугольников;
3) натуральные числа делятся на однозначные, двузначные и трехзначные;
4) параллелограммы могут быть прямоугольниками, квадратами и ромбами.
30. Является ли отношение «выражения х и у имеют одинаковое числовое выражение» на множестве числовых выражений отношением эквивалентности? На какие классы разбивает это отношение заданное множество числовых выражений.
31. Перечислите свойства множества целых неотрицательных чисел N 0.
32. С помощью метода математической индукции докажите, что для любого целого неотрицательного числа n выражение (4 n +15 n -1) делится на 9.
33. Докажите методом математической индукции, что для любого натурального числа  .
.
34. При делении чисел a, b и c на 7 получаются остатки 1, 4 и 5 соответственно. Какой остаток при делении на 7 дает число a+b+c?
1) 6; 2) 3; 3) 0; 4) 7.
35. Правила деления суммы на число и разности на число.
36. Решите задачу и обоснуйте выбор действий, используя терминологию: а) теоретико-множественную; б) принятую в начальном курсе математики.
Для школьного сада привезли 24 саженца яблонь и 6 саженцев груш. Их посадили поровну в 6 рядов. Сколько саженцев посадили в каждом ряду?
37. Решите различными способами приведенную ниже задачу. Дайте к ней наиболее целесообразную графическую иллюстрацию:
Мост через реку имеет три пролета. Длина первого пролета 24 м. Третий пролет на 12 м длиннее первого, а второй на 7 метров короче первого. Найдите длину моста
38. Запишите число 6455 в восьмеричной системе счисления:
1) 144678; 2) 12568; 3) 55628; 4) 272338.
39. Запишите число 18769 в двоичной системе счисления:
1) 10001012; 3) 101101001102;
2) 100000112; 4) 10112.
40. Найдите значение выражения (412136:456):
1) 5136; 2) 1236; 3) 236; 4) 5026.
41. Число тогда и только тогда делится на 9, когда:
1) произведение его цифр делится на 9;
2) сумма его цифр делится на 9;
3) последние две цифры образуют число, делящееся на 9;
4) если оно оканчивается нечетной цифрой.
42. Не выполняя сложения, установите, делится ли на 36 сумма: 1872+23152.
43. Докажите, что разность квадратов двух последовательных натуральных чисел есть число нечетное.
44. Множество N 0 разбивается на попарно непересекающиеся подмножества:
1) числа простые и составные;
2) числа простые, составные и 0;
3) простые, составные и 1;
4) простые, составные, 1 и 0.
45. Простых чисел в промежутке от 1 до 35 всего:
1) 25; 2)11; 3)12; 4)13.
46. Каноническим разложением числа 84 является:
1) 23×3×7; 2)4×21; 3)22×3×7; 4)2×42.
47. НОК для чисел 5, 14 и 35 равно:
1) 70; 2)35; 3)140; 4)210.
48. Найдите все числа вида  , делящиеся на 25:
, делящиеся на 25:
1) 51730, 51710, 51780; 3) 25;
2) 517700; 4) 51700, 51725, 51750, 51775.
49. В чем заключается алгоритм Евклида?
50. Определите, какие из чисел 471, 247 и 253 являются простыми, а какие составными?
51. Найдите НОД(а,b) и НОК (а,b) чисел а =548 и b =2466, представив их в каноническом виде.
52. Найдите НОД(а,b) чисел а =548 и b =2466 с помощью алгоритма Евклида.
53. На новогодней елке ребята получили одинаковые подарки. Во всех подарках было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке?
54. Изобразить на координатной прямой решение уравнения  .
.
55. Вычислить 18  + 16
+ 16  –
– 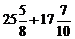 .
.
1) 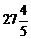 ; 2)
; 2) 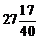 ; 3)
; 3)  ; 4)
; 4)  .
.
56. Решите уравнение 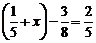 .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
57. Найдите произведение 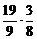 .
.
1)  ; 2)
; 2) 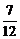 ; 3)
; 3)  ; 4)
; 4) 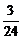 .
.
58. Выполните деление  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 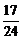 .
.
59. Найдите значение выражения  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
60. Сократите дробь  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
61. Сравните  и
и 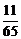 .
.
1) >; 2) <; 3) =; 4) ³.
62. Представьте в виде несократимой обыкновенной дроби 6,2(7).
1) 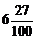 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
63. Сравните 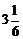 и
и  .
.
1) >; 2) <; 3) =; 4)  .
.
64. Выполните сложение  .
.
1)  ; 2)
; 2) 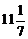 ; 3)
; 3)  ; 4)
; 4)  .
.
65. Запишите коммутативный закон сложения положительных рациональных чисел и докажите его.
66. Докажите, что:  .
.
67. В трех цехах завода работает 2740 человек. Во втором цехе работает на 140 человек больше, чем в первом, а в третьем цехе – в 1,2 раза больше, чем во втором. Сколько человек работает в каждом цехе?
68. Докажите, что если дробь  сократима, то дробь
сократима, то дробь  тоже сократима.
тоже сократима.
69. Найдите пересечение и объединение множества натуральных чисел и множества положительных действительных чисел.
70. Найдите значение выражения  .
.
71. Каким числом (рациональным или иррациональным) является значение выражения:
 .
.
72. Найдите приближенное значение суммы х + y, разности х – y, произведения х·y, частного х: y, с двумя верными десятичными знаками после запятой, если х = 0,666…, у = 0, 57079…
73. Вычислите результат с точностью до сотых 4, 723 + 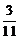 .
.
74. Вычислить  .
. 
75. Найдите область определения функцииy = 5 x2 – 4.
1) (–  ; +
; +  ); 2) [0; +
); 2) [0; +  ); 3) (–
); 3) (–  ; 0); 4) [– 4; +
; 0); 4) [– 4; +  ).
).
76. Укажите число, не принадлежащее области определения функции y =  .
.
1) 4; 2) 5; 3) 3; 4) 1.
77. Найдите область значений функции y = 6 cos 2 x.
1)[2; 6]; 2)[– 12; 12]; 3)[– 6; 6]; 4)[6; 2].
78. Выяснить, является ли четной или нечетной функция y = x 4 + 3 x 2.
1) является четной;
2) является нечетной;
3) является ни четной, ни нечетной;
4) не является четной.
79. Что является графиком данной функции x 2 + 2 x + y 2 = 24.
1) окружность; 2) парабола; 3) гипербола; 4) прямая.
80. Найти интервалы возрастания и убывания функции y = x 2 – x..
81. Укажите множество значений переменной x, при которых выражение имеет смысл 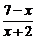 .
.
1) [-2; 7]; 3) [- 2; 2);
2) (– ¥; – 2)  (- 2; + ¥); 4) [- 7; 2].
(- 2; + ¥); 4) [- 7; 2].
82. Решите уравнение 3 x + 7 = 2 x – 4.
1) – 9; 2) – 11; 3) – 13; 4) 11.
83. Найти корни уравнения 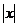 = 4.
= 4.
1) 4; 2) – 4; 3) –4; 4; 4) 2.
84. При каких значениях x являются тождествами следующие равенства
8 x + 9 +  = 8 x + 9.
= 8 x + 9.
85. Найдите множество действительных корней уравнения (3 x – 1) (x + 2) (x – 4) = 0.
86. Найдите множество решений уравнения  = х – 4.
= х – 4.
87. Решите систему уравнений  .
.
88. Решите неравенство 4 –  x >
x >  ∙(4 x – 3).
∙(4 x – 3).
89. Решите неравенство относительно переменной x a (x + 2) > x +1.






