Как в практической жизни, так и в теоретических рассуждениях часто приходится выбирать из нескольких множеств элементы и образовывать из них новые множества, устанавливать различные отношения между имеющимися множествами.
Особый интерес представляют отношения между множествами, имеющими одинаковую природу элементов.
I. Отношение нестрогого включения.
Рассмотрим пример. Пусть А – множество всех учащихся данного класса, В – множество учащихся этого класса, которые успевают по всем предметам.
Выясним зависимость между принадлежностью одного и того же элемента множествам А и В.
Известно, что х Î В. Можно ли утверждать, что х Î А? (Да). Может ли быть, что х Î В, но х Ï А? (Нет, не может).
Заметим, что каждый элемент множества В является элементом множества А. В этом случае говорят, что В является подмножеством (частью) множества А.
Определение. Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А. Обозначается это так: В 
А. (Символ обозначает отношение нестрогого включения).
В этом случае говорят также, что множество В включается в множество А, или множество А включает множество В, а также, что множества А и В находятся в отношении нестрогого включения.
П р и м е р ы.
1) Множество учащихся некоторого класса, изучающих английский язык, является подмножеством множества всех учащихся этого класса;
2) Множество книг по математике в некоторой библиотеке является подмножеством множества книг этой библиотеки;
3) Множество прямоугольников включается в множество параллелограммов.
Чтобы наглядно изображать множества и отношения между множествами рисуют геометрические фигуры, которые находятся между собой в этих отношениях.
Изображение множеств с помощью множеств точек плоскости, ограниченных замкнутыми кривыми, называется диаграммой Эйлера-Венна[1]. На рис. 1 дана диаграмма Эйлера-Венна для случая, когда В А.
 |
А
В
Рис. 1
Свойства отношения нестрогого включения.
1°. Всякое множество А есть подмножество самого себя т.е. для всякого А верно А 
А.
2°. Для любых множеств А, В, С, если А 
В и В С, то А С. Очевидно, что часть части данного множества всегда является его частью.
3°. Пустое множество считается подмножеством любого множества А:
Æ А.
II. Отношение равенства.
Отношение равенства является частным случаем нестрогого включения.
Определение. Множества А и В, состоящие из одних и тех же элементов, называют равными.
Равенство множеств обозначают так: А = В. Из определения равенства множеств следует, что важен лишь состав множества, и не существенен порядок следования элементов множества.
Например, множества А = { а, в, с }, В = { в, а, с }, С = { с, а, в } равны между собой.
П р и м е р ы.
1) А = {1, 22, 32, 42} и В = {1, 
, 
, 
}.
Эти множества равны, т. к. они состоят из чисел 1, 4, 9, 16.
2) А – множество ромбов с прямыми углами;
В – множество квадратов. А = В.
Равенство множеств характеризуется тремя свойствами (этими свойствами обладает и отношение равенства чисел).
1°. Для всякого множества А справедливо А = А.
2°. Для любых двух множеств А, В, если А = В, то В = А.
3°. Для любых 3-х множеств А, В, С, если А = В и В = С, то А = С.
Заметим, что очевидно А = В тогда и только тогда, когда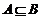 
и 
.
III. Отношение строгого включения.
Если в отношении «множество В является подмножеством множества А» () хотят подчеркнуть, что А содержит и другие элементы, кроме элементов из В, то говорят, что В строго включено в А или является правильной частью множества А.
Определение. Если каждый элемент множества В является элементом множества А, и в А существует хотя бы один элемент не принадлежащий множеству В, то множество В строго включается в множество А. Обозначается 
.
Множество В в этом случае называется собственным подмножеством множества А, т.е. 
если и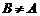 
.
Так, например, N Ì Z, Z Ì Q, Q Ì R.
