Контрольная работа для студентов заочного отделения

Контрольная работа

Тема: Множества и операции над ними. Соответствия, отношения, отображения.
Элементы комбинаторики

Образец выполнения заданий контрольной работы

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (–3; 6), В = [5; 7); б) Изобразите на координатной плоскости множества А ´ В, В ´ А, А ², В ², если А, В – множества из пункта а); в) Докажите, что для любых множеств А, В, С верно соотношение: (А  С)\ В Ì (A \ B) C. Изобразите данное соотношение на кругах Эйлера.

Р е ш е н и е. а) Изобразим данные множества на числовой прямой (см. рис. 1):

-3                                                      5       6       7  х

Рис. 1

Множество чисел, принадлежащих одновременно обоим множествам – это промежуток [5, 6), следовательно А В = (–3; 6) [5; 7) = [5; 6). Множество чисел, принадлежащих хотя бы одному из множеств – это промежуток (–3; 7), следовательно А В = (–3; 6) [5; 7) = (–3; 7). Множество чисел, принадлежащих множеству А и не принадлежащих множеству В – это промежуток (–3, 5), следовательно, А \ В = (–3; 6) \ [5; 7) = (–3; 5). Множество чисел, принадлежащих множеству В и не принадлежащих множеству А – это промежуток [6, 7), следовательно В \ А = [5; 7) \ (–3; 6) = [6; 7).

б) А ´ В (см. рис. 2), В ´ А (см. рис. 3), А ² (см. рис. 4), В ² (см. рис. 5).

у                                                                y

 

 

 

                                                                       x                                                                        x

 

 

 

Рис. 2                                                                           Рис. 3

y                                                                           y

 

 

x                                                                               x

 

Рис. 4                                                                  Рис. 5

 

в) Д о к а з а т е л ь с т в о. Пусть x Î (А   С) \ В, тогда по определению разности множеств, х Î А   С и x Ï В. Раз x Î А   С, то согласно определению объединения множеств, имеем х Î А или х Î С. Если х Î А, то поскольку х Ï В, имеем, что х Î А \ В и, следовательно, х Î (А \ В) С.

Если же х Î С, то, по определению объединения множеств, x Î (А \ В) С. Таким образом, мы показали, что всякий элемент множества А   C \ В является элементом множества (А \ В) С, значит, (А С) \ В Ì(А \ В) С. Данное соотношение можно изобразить на кругах Эйлера (см. рис. 6).

А         С                            А       С

В                                           В

 

(А  С) \ В                             (А \ В) С

Рис. 6

Задание 2. Между элементами множества Х = { Ф₁, Ф₂, Ф₃, Ф₄, Ф₅, Ф₆ } – прямоугольников (см. рис. 7) и множества Y = {4, 5, 6, 8, 16}, задано бинарное соответствие Р – «прямоугольник х имеет площадь, равную у», х Î Х,    у Î Y.

а) Найдите область определения D (P) и область значений E (P) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) укажите образ прямоугольника Ф₂ и прообраз числа 8 при соответствии Р.

Ф₁                           Ф₂

 

 

Ф₃                   Ф₄

 

Ф₅                   Ф₆

 

Рис. 7

Р е ш е н и е. а) Областью определения соответствия Р является множество D (Р) = {Ф₁, Ф₂, Ф₃, Ф₄, Ф₅, Ф₆}, а областью значений – множество E (P) = {8, 16, 5, 4}. Область определения соответствия Р совпадает с множеством Х (областью отправления), а область значений является подмножеством множества Y (области прибытия).

б) Изобразим элементы множеств Х и Y в виде точек и построим граф соответствия Р (см. рис. 8).

X                            Y

Ф₁·                           ·4

Ф₂·                           ·5

Ф₃·                           ·6

Ф₄·                           ·8

Ф₅·                           ·16

Ф₆·

 

Рис. 8

в) Граф обратного соответствия Р ^-1 на рис. 9.

X                            Y

Ф₁·                           ·4

Ф₂·                           ·5

Ф₃·                           ·6

Ф₄·                           ·8

Ф₅·                           ·16

Ф₆·

Рис. 9

д) Образом элемента Ф₂ из множества Х является число 16 из множества Y: Р (Ф ₂) = 16. Прообразом числа 8 из множества У является прямоугольники Ф₁ из множества Х: Р ^-1(8) = { Ф ₁}.

г) Граф противоположного соответствия на рис. 10.

X                            Y

Ф₁·                            ·4

Ф₂·                            ·5

Ф₃·                            ·6

Ф₄·                            ·8

Ф₅·                            ·16

Ф₆·

Рис. 10

Задание 3. Отношение Р – «число х является квадратом числа у» задано на множестве

Х = {2, –1, 1, 2, 4}.

а) Постройте граф и график отношения Р;

б) задайте отношение Р при помощи уравнения;

в) постройте графики отношений  и Р^-1.

Р е ш е н и е. а) Изобразим все элементы множества Х точками на плоскости и соединим стрелками те пары чисел, которые находятся в отношении Р. Например, 1 является квадратом числа –1, т.е. 1 = (–1)², поэтому проводим стрелку от точки, изображающей число 1, к точке, изображающей число –1. Так как число 1 является квадратом 1, то около точки, изображающей число 1, должна быть стрелка, начало и конец которой совпадают (петля). Аналогично рассматриваются и другие элементы множества. В итоге получим граф (см. рис. 11).

Чтобы построить график отношения Р, выберем на плоскости прямоугольную систему координат, на каждой из осей отметим точками элементы множества Х и изобразим точками на плоскости все пары чисел, находящихся в этом отношении, а именно: {(1; –1), (1; 1), (4; –2), (4; 2)}, где первые элементы пар являются абсциссами, а вторые – ординатами точек плоскости (см. рис. 12).

б) Из отношения «число х является квадратом числа у» следует, что х = у². Это и будет задание отношения Р при помощи уравнения, где х Î Х, у Î У.

-2 -1   4                        1   2   Рис. 11

Рис. 12

в) Отношение , противоположное отношению Р, может быть задано так: «число х не является квадратом числа у». Множество пар чисел из множества Х, находящихся в отношении , есть      {(–2; –2), (–2; –1), (–2; 1), (–2; 2), (–2; 4), (–1; –2), (–1; 1), (–1; –1), (–1; 2), (–1; 4), (1; –2), (1; 2), (1; 4), (2; –2), (2; –1), (2; 2), (2; 4), (2; 1), (4; –1), (4; 1), (4; 4)}. Его график изображен на рис. 13.

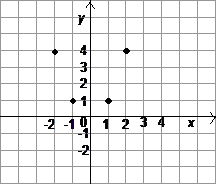
Отношение Р ^-1, обратное отношению Р, можно задать при помощи предложения с двумя переменными: «число х есть корень квадратный из числа у», а также можно задать, записав множество всех пар чисел из множества Х, находящихся в отношении Р ^-1: {(–1; 1), (1; 1), (–2; 4), (2; 4)}. Его график изображен на рис. 14.

Рис. 13                                                                  Рис. 14

Задание 4. На множестве отрезков задано отношение Р: «отрезок х равен отрезку у». Определите свойства этого отношения.

Р е ш е н и е. Отношение Р рефлексивно, поскольку любой отрезок х равен самому себе. Отношение Р симметрично, поскольку для любых двух отрезков х и у имеем: если отрезок х равен отрезку у, то отрезок у равен отрезку х. И, наконец, отношение Р транзитивно, поскольку для любых трех отрезков х, у, z, если отрезок х равен отрезку у, а отрезок у равен отрезку z, то отрезок х равен отрезку z. Значит отношение Р является отношением эквивалентности (по определению).

Задание 5. На множестве А = {3, 4, 8, 5} задано отношение Р = {(3; 3), (3; 4), (4; 3), (4; 4), (5; 5), (4; 5), (5; 4), (8; 8), (3; 5), (5; 3)}. Является ли это отношение: а) отношением эквивалентности; б) отношением порядка?

Р е ш е н и е. а) Отношение Р является отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. Проверим указанные свойства. По определению: отношение Р рефлексивно на некотором множестве, если выполняется условие хРх для всех элементов х этого множества. Для всех элементов множества А это условие выполняется, так как в график отношения входят пары (3; 3), (4; 4), (5; 5), (8; 8).

Отношение Р симметрично на некотором множестве, если для любых элементов х и у из этого множества выполняется условие хРу и уРх. Это условие выполняется, так как в график отношения входят пары (3; 4) и (4; 3), (4; 5) и (5; 4), (3; 5) и (5; 3). Значит, отношение Р симметрично.

Отношение Р транзитивно, если для любых трех элементов х, у, и z, принадлежащих некоторому множеству, из выполнения условий хРу и уРz следует выполнение условия хРz. Отношение Р транзитивно, так как из 3 Р 4 и 4 Р 5 следует 3 Р 5 (в график отношения входят все три пары: (3; 4), (4; 5),  (3; 5). Аналогично, парам (5; 4) и (4; 3) соответствует пара (5; 3).

Итак, все три свойства для отношения Р выполняются, значит, отношение P является отношением эквивалентности.

б) Отношение Р в множестве А называют отношением строгого порядка, если оно асимметрично и транзитивно, и нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно. Данное отношение Р рефлексивно, симметрично и транзитивно.

Значит, отношение Р не является отношением нестрогого порядка, и не является отношением строгого порядка.

Задание 6. В вазе стоят 10 красных и 4 розовые гвоздики. Сколькими способами можно выбрать 3 цветка из вазы?

Р е ш е н и е. 3 цветка из вазы можно выбрать только из числа красных гвоздик (из множества А, состоящего из десяти элементов нужно образовать его 3-х элементные части), т.е. нужно сосчитать число трехэлементных частей 10-ти элементного множества – это есть число сочетаний .

3 цветка из вазы можно выбрать из числа четырех розовых гвоздик, аналогичные рассуждения приводят к тому, что будет .

3 цветка из вазы можно выбрать, взяв 2 красные гвоздики и 1 розовую гвоздику. 2 красные гвоздики можно выбрать из десяти  способами. Одну розовую гвоздику можно выбрать  способами. Ясно, что 2 красные и 1 розовую гвоздику можно выбрать ·  способами.

3 цветка из вазы можно выбрать, взяв 1 красную гвоздику и 2 розовые гвоздики ·  способами.

Всего число способов, которыми можно выбрать три гвоздики из вазы, равно сумме:

+ · + · + =  = 120 + 180 + 60 + 4 = 364.

Варианты контрольной работы

Вариант 1

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (–3, 3], В = (1, 5).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А ², В ², если А, В – множества из пункта а).

в) Докажите, что множества А \ В и А \ (А  В) равны и изобразите их на кругах Эйлера-Венна. Здесь А и В – произвольные множества.

Задание 2. Между элементами множества Х = { а, б, в, г, д, е } и множества Y ={«сад», «дом», «бор», «вода»} задано бинарное соответствие Р: «буква х входит в слово у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (а), Р ^-1(«сад»).

Задание 3. Отношение Т: «число х в 3 раза меньше числа у» задано на множестве А ={1, 2, 3, 6, 18}.

а) Постройте граф и график отношения Т;

б) задайте Т при помощи уравнения;

в) постройте график противоположного отношения  и график обратного отношения Т ^-1.

Задание 4. На множестве учащихся класса задано отношение «учащийся х старше по возрасту учащегося у». Определите свойства заданного отношения.

Задание 5. На множестве Х = {2, 4, 6, 8} задано отношение Р = {(2, 2), (4, 4), (6, 6), (8,8), (6, 4), (4, 2), (6, 2), (2, 4), (2, 6), (4, 6)}. Определите, является ли Р: а) отношением эквивалентности? б) отношением порядка?

Задание 6. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-ый и 2-ой тома: а) стояли рядом; б) не стояли рядом?

Вариант 2

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = [2, 6), В = (-¥, 3).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А ², В ², если А, В – множества из пункта а).

в) Докажите, что множества (А \ В) \ С и (А \ С) \ В равны и изобразите их на кругах Эйлера-Венна. Здесь А, В, С – произвольные множества.

Задание 2. Между элементами множества Х ={–2, –1, 0, 1, 2, 3} и множества Y ={–1, 0, 1, 2} задано бинарное соответствие Р: «модуль числа х равен числу у» (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (–2), Р (0), Р^{- 1}(2).

Задание 3. Отношение S: «число х в 2 раза больше числа у» задано на множестве В = {1,2,3,4,6}.

а) Постройте граф и график отношения S;

б) задайте отношение S при помощи уравнения;

в) постройте график противоположного отношения  и график обратного отношения S ^-1.

Задание 4. На множестве людей задано отношение «человек х на 2 см выше человека у». Определите свойства заданного отношения.

Задание 5. На множестве А = {6, 7, 8, 9} задано отношение Т = {(6, 6), (6, 7), (7, 6), (6, 8), (7, 7), (7, 8), (8,8), (8,6), (8, 7), (9, 9)}. Определите, является ли Т: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Сколько всего натуральных чисел можно составить из цифр {0, 1, 3, 5, 7}, не повторяя цифры в числе?

Вариант 3

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (0, 8), В = (–4, 3).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества А \(В  С) и (А \ В)  (А \ С) равны и изобразите их на кругах Эйлера-Венна. Здесь А, В, С – произвольные множества.

Задание 2. Между элементами множества Х = { х + 2 = 3, 4 х – 6 = 2, (х – 1) (х – 2) = 0,                 3(х – 1) = 3 х + 2} и множества Y = {–1, 0, 1, 2} задано бинарное соответствие Р: «уравнение х имеет корень у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (х + 2 = 3), Р ^-1(2).

Задание 3. Отношение К: «число х на два больше числа у» задано на множестве В = {1, 2, 3, 5, 7, 9}.

а) Постройте граф и график отношения К;

б) задайте К при помощи уравнения;

в) постройте график противоположного отношения  и график обратного отношения К ^-1.

Задание 4. На множестве людей задано отношение «человек х родился в том же году, что и человек у». Определите свойства заданного отношения.

Задание 5. На множестве Х = {2, 4, 6, 8} задано отношение М ={(2, 2), (4, 4), (6, 6), (8, 8), (2, 4), (4, 8), (2,6), (4, 6), (6, 8)}. Определите, является ли М: а) отношением эквивалентности? б) отношением порядка?

Задание 6. В группе 25 студентов. Они обменялись друг с другом фотографиями. Сколько всего фотографий было роздано?

Вариант 4

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (3, 8), В = (–4, 5].

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества (А \ В)  (В \ А) и (В \ А)  (А \ В)равны и изобразите их на кругах Эйлера-Венна. Здесь А, В – любые множества.

Задание 2. Между элементами множества Х = {–2, 2, –1, 1, 0} и множества Y ={–1, 0, 1, 2, 3, 4} задано соответствие Р: «квадрат числа х равен у», (х Î Х, y Î Y).

а) Найдите область определения D (Р)и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (–2), Р^{- 1}(1).

Задание 3. Отношение М: «число х на 1 больше числа у» задано на множестве А = {2, 3, 4, 6, 7}.

а) Постройте граф и график отношения М;

б) задайте М при помощи уравнения;

в) постройте график противоположного отношения  и график обратного отношения М^-1.

Задание 4. На множестве отрезков задано отношение «отрезок х длиннее отрезка у». Определите свойства заданного отношения.

Задание 5. На множестве С = {3, 2, 5, 6} задано отношение К ={(2, 3), (3, 6), (2, 6), (5,2), (5, 6), (5, 3)}. Определите, является ли К: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Сколько можно составить из простых делителей числа 2310 составных чисел, которые имеют только два простых делителя?

Вариант 5

Задание 1. а) Найдите и изобразите на числовой прямой множества А  В, А  В, А \ В, В \ А, если А = (–1, 2], В = [–3, 1).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества (А \ В)  (В \ А) и (А  В) \ (В  А) равны и изобразите их на кругах Эйлера-Венна. Здесь А и В - произвольные множества.

Задание 2. Между элементами множества Х = {«стол», «пол», «кол»} и множества Y ={а, о, к, л} задано бинарное соответствие Р: «в слово х входит буква у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (стол), Р ^-1(k).

Задание 3. Отношение S: «число х на 1 меньше числа у» задано на множестве С ={4, 5, 7, 8, 9}.

а) Постройте граф и график отношения S;

б) задайте S при помощи уравнения;

в) постройте график противоположного отношения  и график обратного отношения S ^-1.

Задание 4. На множестве геометрических фигур задано отношение «фигура х является частью фигуры у». Определите свойства этого отношения.

Задание 5. На множестве А = {8, 5, 12, 7} задано отношение Р: «х > у». Определите, является ли отношение Р: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Сколько человек участвовало в шахматном турнире, если известно, что каждый участник сыграл с каждым из остальных по одной партии, а всего было сыграно 210 партий.

Вариант 6

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если В = (2, +¥), А = [–4, 5).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества А \ (В \ С) и А \ (В \ В  С) равны и изобразите их на кругах Эйлера-Венна. Здесь А и В – произвольные множества.

Задание 2. Между элементами множества Х = {1, 2, 3, 4, 5} и множества Y = {1, 3, 4, 16, 9, 25} задано бинарное соответствие Р: «квадрат со стороной х имеет площадь, равную у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (3), Р ^-1(25).

Задание 3. Отношение М: «число х в 3 раза меньше числа у» задано на множестве А ={1, 3, 9, 27}.

а) Постройте граф и график отношения М;

б) задайте М при помощи уравнения;

 в) постройте график противоположного отношения  и график обратного отношения М ^-1.

Задание 4. На множестве N натуральных чисел задано отношение Р: «число b следует за числом а». Определите свойства заданного отношения.

Задание 5. На множестве D = {3, 6, 9, 12} задано отношение Т ={(3, 3), (6, 6), (9, 3), (12, 3), (9, 9), (12, 12)}. Определите, является ли Т: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Из 10 различных цветков нужно составить букет так, чтобы в него входило не менее 3 цветков. Сколько способов существует для составления такого букета?

Вариант 7

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А =[–5, 1) и В = [–2, 2].

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества А   (В \ А) и А  В равны и изобразите их на кругах Эйлера-Венна. Здесь А и В – произвольные множества.

Задание 2. Между элементами множества Х = {1, 2, 3, 4} и множества Y = {2p, 4p, 6p, 8p} задано бинарное соответствие Р: «окружность радиуса х имеет длину, равную у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) множества Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия.

д) найдите Р (1), Р ^-1(8p);

Задание 3. Отношение S: «число х на 2 меньше числа у» задано на множестве А = {2, 4, 6, 8, 10}.

а) Постройте граф и график отношения S;

б) задайте S при помощи уравнения;

в) постройте график обратного отношения S ^-1 и график противоположного отношения .

Задание 4. На множестве N натуральных чисел задано отношение Т: «число х кратно числу у». Определите свойства заданного отношения.

Задание 5. На множестве С = {3, 6, 10} задано отношение S: «х ³ у». Определите, является ли S: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Из 12 лотерейных билетов, среди которых находится 4 выигрышных, берут 6 билетов. Сколькими способами можно взять 6 билетов так, чтобы среди них находился хотя бы один выигрышный?

Вариант 8

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = [–3, 3), В = (–2, 5].

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а).

в) Докажите, что множества А \ В и А  В равны и изобразите их на кругах Эйлера-Венна. Здесь А и В – произвольные множества.

Задание 2. Между элементами множества Х = {45, 0, 1, 66, 122} и множества Y = {2, 3, 4, 5, 6} задано бинарное соответствие Р: «число х кратно числу у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (45), Р ^-1(5).

Задание 3. Отношение S: «число х на 4 больше числа у» задано на множестве Х = {3, 7, 11,15}.

а) Постройте граф и график отношения S;

б) задайте S при помощи уравнения;

в) постройте график обратного отношения S ^-1 и график противоположного отношения .

Задание 4. На множестве людей задано отношение Т: «человек х живет на той же улице, что и человек у». Определите свойства этого отношения.

Задание 5. На множестве В = {1, 2, 3} задано отношение Р = {(1, 2), (1, 1), (2, 2), (2, 1), (3, 1), (3, 3), (1, 3)}. Определите, является ли Р:

а) отношением эквивалентности? б) отношением порядка?

Задание 6. Имеется 12 различных сортов конфет. Сколькими способами можно составить из них набор, если в наборе должно быть четное число сортов конфет?

Вариант 9

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (–2, 2], В = [–6, 0).

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а);

в) Докажите, что множества (А  В) / С и А  (В / С) равны и изобразите их на кругах Эйлера-Венна. Здесь А, В, С – произвольные множества.

Задание 2. Между элементами множества Х = {1, 2, 3, 4, 5} и множества У = {p, 4p, 9p, 16p} задано бинарное соответствие Р: «круг радиуса х имеет площадь, равную у», (х Î Х, y Î Y).

а) Найдите область определения D (Р)и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия;

г) постройте граф противоположного соответствия;

д) найдите Р (3), Р (5), Р ^-1(4p).

Задание 3. Отношение Т: «число х на 5 больше числа у» задано на множестве У = {1, 6, 11, 16}.

а) Постройте граф и график отношения Т;

б) задайте Т при помощи уравнения;

в) постройте график обратного отношения Т^{- 1} и график противоположного отношения .

Задание 4. На множестве N натуральных чисел задано отношение S: «число х имеет ту же четность, что и число у». Определите свойства заданного отношения.

Задание 5. На множестве А = {2, 4, 6, 8} задано отношение К = {(2, 4), (2, 6), (2, 8), (2, 2), (4, 4), (4, 8), (6, 6), (8, 8)}. Определите, является ли К: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Расписание одного дня содержит 5 уроков. Определите количество таких расписаний при выборе из 11 дисциплин.

Вариант 10

Задание 1. а) Найдите и изобразите на числовой прямой множества А В, А В, А \ В, В \ А, если А = (–¥, 2), В = [1, 4].

б) Найдите и изобразите на координатной плоскости множества А ´ В, В ´ А, А², В², если А, В – множества из пункта а);

в) Докажите, что множества (А \ В)  (А  В)и А равны и изобразите их на кругах Эйлера-Венна. Здесь А, В – произвольные множества.

Задание 2. Между элементами множества Х = {3 · 5;  9 + 2;  0: 7;  4²; 6 · 0} и множества Y ={0, 1, 10, 11, 15, 16} задано бинарное соответствие Р: «значение выражения х равно числу у», (х Î Х, y Î Y).

а) Найдите область определения D (Р) и множество значений Е (Р) соответствия Р;

б) постройте граф соответствия Р;

в) постройте граф обратного соответствия.

г) постройте граф противоположного соответствия;

д) найдите Р (0: 7), Р ^-1(16).

Задание 3. Отношение S: «число х на 6 больше числа у» задано на множестве С = {1, 6, 7, 12, 13}.

а) Постройте граф и график отношения S;

б) задайте S при помощи уравнения;

в) постройте график обратного отношения S ^-1 играфик противоположного отношения .

Задание 4. На множестве людей задано отношение Т: «быть дочерью». Определите свойства заданного отношения.

Задание 5. На множестве Х = { t, l, m, n } задано отношение Р = {(t, l), (t, m), (t, t), (l, t), (l, l), (l, m), (m, t), (m, l), (m, m), (n, n)}. Определите, является ли Р: а) отношением эквивалентности? б) отношением порядка?

Задание 6. Из 10 юношей, 8 мальчиков и 5 девушек нужно составить шахматную команду, в которую бы входили 4 юноши, 1 мальчик и 2 девушки. Сколькими способами это можно сделать?