91. Решите неравенство  > 1.
> 1.
92. Найдите множество решений системы неравенств 
93. Найдите множество решений совокупности 
94. Как разрезать прямоугольник на два такие треугольника, из которых можно было бы составить параллелограмм?
95. Известно, что  (а)= k,
(а)= k,  (b)= k 1,
(b)= k 1,  (с)= k 2. Отрезок а = b + c. Найти
(с)= k 2. Отрезок а = b + c. Найти  (е 1).
(е 1).
1) 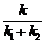 ; 2)
; 2) 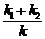 ; 3) k 1· k + k 2· k; 4) k 1+ k 2.
; 3) k 1· k + k 2· k; 4) k 1+ k 2.
96. Известно, что 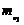 (а)= а 1,
(а)= а 1,  (а)= а 2,
(а)= а 2,  (b)= b 2. Найти
(b)= b 2. Найти 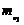 (b).
(b).
1)  ; 2)
; 2)  ; 3) b 2+
; 3) b 2+  ; 4) а 1+
; 4) а 1+  .
.
97. Выполните с помощью циркуля и линейки основное построение: «Построение угла, равного данному». Описание построения выполните по шагам, сводя каждый шаг к соответствующему постулату построения.
98. Изобразите и назовите многогранник, имеющий наименьшее число граней. Сколько у него ребер, вершин, диагоналей? Проверьте выполнение теоремы Эйлера для этого многогранника.
99. Число граней и их форма у октаэдра:
1) 12 пятиугольников; 3) 8 треугольников;
2) 6 квадратов; 4) 20 треугольников.
100. Изображением правильного треугольника при параллельном проектировании является:
1) правильный треугольник; 3) равнобедренный треугольник;
2) произвольный треугольник; 4) разносторонний треугольник.
ВАРИАНТ 2
1. Если а и b – различные действительные числа (а < b), то числовое множество  обозначается в виде:
обозначается в виде:
1) [ a, b ]; 2){ a,b }; 3) (a, b); 4)(-¥,+ ¥)
2. Множество, состоящее из всех пар элементов (а, в) таких, что а ÎА, в ÎВ, называется:
1) пересечением множеств А и В и обозначается А Ç В;
2) объединением множеств А и В и обозначается А È В;
3) разностью множеств А и В и обозначается А \ В;
4) декартовым произведением двух множеств А и В и обозначается А ´ В.
3. Найти дополнение множества А до множества R, если А =(-¥; 2).
1)  2)
2)  ; 3)
; 3)  ; 4)
; 4)  Æ.
Æ.
4. Запишите для множеств А и В закон поглощения.
5. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. Постройте круги Эйлера для данных множеств и отметьте штриховкой область, изображающую множество  .
.
6. Укажите характеристическое свойство элементов множества Y=K \  , если K= { x/ x Î R, x> 0}, L={x/ x Î R, 17 <x< 25}, M= { x/ x Î R, x ³ 23}.
, если K= { x/ x Î R, x> 0}, L={x/ x Î R, 17 <x< 25}, M= { x/ x Î R, x ³ 23}.
7. Из 25 учащихся класса 15 увлекаются математикой, а 8 – русским языком. Каким может быть число учащихся, увлекающихся обоими предметами? Хотя бы одним предметом?
8. Проиллюстрируйте на кругах Эйлера, что для любых множеств А, В и С верно равенство: (А\В) Ç (А\С)=А\(ВÈС).
9. Изобразите на координатной плоскости А´В, если А=(-1;2], В=[1;3].
10. Правило суммы в комбинаторике для двух пересекающихся множеств формулируется как:
1) n (А È В)= n (A)· n (B); 3) n (А È В)= n (A) n (B)- n (А È В);
2) n (А È В)= n (A)+ n (B)- n (А Ç В); 4) n (А È В)= n (A)+ n (B).
11. m! равен:
1) произведению всех целых чисел;
2) числу перестановок из m элементов;
3) сумме всех натуральных чисел от 0 до m;
4) нулю.
12. Неупорядоченные k -элементные подмножества, составленные из элементов m-элементного множества X, называются:
1) размещениями с повторениями;
2) сочетаниями без повторений;
3) перестановками без повторений;
4) размещениями без повторений.
13. Из 100 студентов, изучающих английский и немецкий языки, 80 изучают английский язык, 30 – немецкий. Сколько студентов изучают оба языка?
1) 50 студентов; 3) 20 студентов;
2) 30 студентов; 4) 80 студентов.
14. Размещения без повторений из m по k вычисляются по формуле:
1) m × k; 3) 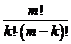 ;
;
2) mk; 4) m (m –1)(m – 2)×...×(m – k +1).
15. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если любую из них в каждом числе использовать не более одного раза?
16. Найдите значение выражения:  .
.
17. Вычислите:  .
.
18. Сколько нечетных чисел можно составить из цифр числа 34526, если каждую цифру использовать не более одного раза?
19. Назовите несколько элементов, принадлежащих объему понятия «многоугольник».
20. Высказывание «А и В» называется:
1) конъюнкцией высказываний А и В;
2) дизъюнкцией высказываний А и В;
3) импликацией высказываний А и В;
4) эквиваленцией высказываний А и В.
21. Импликация двух высказываний А и В ложна тогда и только тогда, когда:
1) А – «И», В – «Л»; 3) А – «И», В – «И»;
2) А – «Л», В – «И»; 4) А – «Л», В – «Л»;
22. Сформулируйте правило отрицания и приведите пример умозаключения, которое построено по этому правилу.
23. Составьте таблицу истинности для высказывания: (ĀÙВ)ÞС.
24. Даны предикаты A(x): «x > 3» и B(x): «x < 4».
Найдите множество истинности ТАÚВ предиката А(x)ÚВ(x).
25. Отношение Т: «число x больше числа y» задано на множестве А={2,3,6,8,10}. Постройте граф и график отношения Т, определите его свойства.
26. Если каждый элемент множества Y является образом не более одного элемента из Х, то такое отображение называется:
1) биекцией; 3) сюръекцией;
2) инъекцией; 4) соответствием.
27. Х – множество окружностей плоскости, Y – множество точек этой плоскости. Отношение между множествами X и Y задано так: «окружность x имеет центр y». Равномощны ли множества X и Y? Ответ обоснуйте.
28. Является ли отношение «равно», заданное на множестве дробей отношением эквивалентности?
29. Разбить множество натуральных чисел на классы по свойству: быть четным числом:
1) четные, нечетные; 3) четные и отрицательные;
2) ноль, четные и нечетное; 4) положительные, ноль, отрицательные
30. На множестве отрезков задано отношение М – «иметь одну и ту же длину». Является ли отношение М отношением эквивалентности? На какие классы разбивает это отношение заданное множество отрезков?
31. Сформулируйте метод математической индукции.
32. С помощью метода математической индукции докажите, что для любого целого неотрицательного числа n выражение (32 n +3+5) делится на 8.
33. Докажите методом математической индукции, что для любого натурального числа  .
.
34. При делении чисел a, b и c на 9 получаются остатки 2, 6 и 3 соответственно. Какой остаток при делении на 9 дает число a × b+c?
1) 6; 2) 3; 3) 0; 4) 7.
35. Правило деления произведения на число.
36. Решите задачу и обоснуйте выбор действий, используя терминологию: а) теоретико-множественную; б) принятую в начальном курсе математики.
В школе в 3 аквариумах было по 16 рыбок в каждом. 20 рыбок школьники подарили детскому саду. Сколько рыбок осталось?
37. Решите различными способами приведенную ниже задачу. Дайте к ней наиболее целесообразную графическую иллюстрацию: На 3 платья у портных пошло 12 м материи. Сколько метров материи пойдет на 2 таких же платья?
38. Запишите число 2930 в восьмеричной системе счисления:
1) 144678; 2) 12568; 3) 55628; 4) 272338.
39. Запишите число 34556 в двоичной системе счисления:
1) 10001012; 3) 101101001102;
2) 11001110112; 4) 10112.
40. Найдите значение выражения (123324 ×2024):
1) 2222234; 3) 32303304;
2) 10001234; 4) 33223024.
41. Число тогда и только тогда делится на 3, когда:
1) произведение его цифр делится на 3;
2) сумма его цифр делится на 3;
3) последние две цифры образуют число, делящееся на 3;
4) если оно оканчивается нечетной цифрой.
42. Не производя вычитания, установите, делится ли на 36 разность: 23544-17028.
43. Докажите, что если натуральные числа a и b при делении на 7 дают один и тот же остаток, то разность квадратов этих чисел делится на 7.
44. Наименьший простой делитель составного числа не превосходит:
1)  ; 2) а; 3)
; 2) а; 3)  ; 4)
; 4) 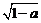 .
.
45. Простых чисел в промежутке от 1 до 50 всего:
1) 25; 2) 11; 3) 15; 4) 13.
46. Каноническим разложением числа 60 является:
1) 22×3×5; 2) 4×15; 3)22×15; 4) 12×5.
47. НОК для чисел 2, 16 и 33 равно:
1) 16; 2) 33; 3) 264; 4) 528.
48. Найдите все числа вида  , делящиеся на 36:
, делящиеся на 36:
1) 56232, 56736; 2)56236; 3)56336; 4) 0.
49. Сформулируйте основную теорему арифметики.
50. Определите, какие из чисел 187, 467 и 133 являются простыми, а какие составными?
51. Найдите НОД (а,b) и НОК (а,b) чисел а =1960 и b =588, представив их в каноническом виде.
52. Найдите НОД (а,b) чисел а =1960 и b =588 с помощью алгоритма Евклида.
53. Имеется 30 зеленых и 42 желтых листов бумаги. Какое наибольшее число комплектов можно сделать из этих листов, если в каждом комплекте должно быть по одинаковому числу зеленых и одинаковому числу желтых листов?
54. Изобразить на координатной прямой решение уравнения 
55. Вычислить  .
.
1) 2; 2) 4; 3)  4) 1.
4) 1.
56. Решите уравнение  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 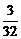 .
.
57. Найдите произведение  .
.
1)  ; 2)
; 2) 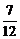 ; 3)
; 3)  ; 4)
; 4)  .
.
58. Выполните деление 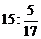 .
.
1)  ; 2)
; 2)  ; 3) 51; 4)
; 3) 51; 4)  .
.
59. Найдите значение выражения  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 
60. Сократите дробь  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
61. Сравните 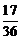 и
и  .
.
1) >; 2) <; 3) =; 4)  .
.
62. Представьте в виде несократимой обыкновенной дроби 13,4(72).
1)  ; 2)
; 2) 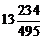 ; 3)
; 3)  ; 4)
; 4)  .
.
63. Сравните  и 2,(571428).
и 2,(571428).
1) >; 2) <; 3) =; 4)³.
64. Выполнить сложение 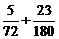 .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
65. Запишите коммутативный закон сложения положительных рациональных чисел и докажите его.
66. Докажите, что  .
.
67. В колхозном саду сливовые деревья составляли  всего количества плодовых деревьев, яблони
всего количества плодовых деревьев, яблони 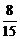 , а остальные 360 деревьев были грушевые. Сколько плодовых деревьев было в колхозном саду?
, а остальные 360 деревьев были грушевые. Сколько плодовых деревьев было в колхозном саду?
68. Докажите, что если дробь  сократима, то дробь
сократима, то дробь  тоже сократима.
тоже сократима.
69. Найдите пересечение и объединениемножества положительных рациональных чисел и множества положительных иррациональных чисел.
70. Найдите значение выражения 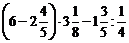 .
.
71. Каким числом (рациональным или иррациональным) является значение выражения  .
.
72. Найдите приближенное значение суммы х+у, разности х–у, произведения х·у, частного х:у с двумя верными десятичными знаками после запятой, если х=  , у = 0,15604.
, у = 0,15604.
73. Вычислите результат с точностью до сотых  .
.
74. Вычислить 
75. Найдите область определения функции y =  .
.
1) (- ¥; 3]; 3) (-¥; 3)  (3; +¥);
(3; +¥);
2) [0; + ¥); 4) (-¥; 3]  (3; +¥).
(3; +¥).
76. Укажите число, не принадлежащее области определения функции y = 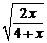 .
.
1) 1; 2) – 2; 3) 2; 4) 3.
77. Найдите область значений функции y =  .
.
1) [- 3; 3]; 2)[- 1; 1]; 3)  ; 4)
; 4)  .
.
78. Выяснить, является ли четной или нечетной функция y =  ;
;
1) является четной;
2) является нечетной;
3) является ни четной, ни нечетной;
4) не является четной.
79. Что является графиком данной функции у – x 2 + 4 x – 2 = 0.
1) окружность; 3) гипербола;
2) парабола; 4) прямая.
80. Найти интервалы возрастания и убывания функции: у = x 2 + 12 х -100.
81. Укажите множество значений переменной х, при которых выражение имеет смысл: 
1) (- 1; 2); 3) (-¥; -1)  (-1; 2)
(-1; 2)  (2;+ ¥);
(2;+ ¥);
2) [-¥;2)  (-1; +¥); 4) (-¥; +¥).
(-1; +¥); 4) (-¥; +¥).
82. Решите уравнение: 
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
83. Найти корни уравнения 
1) -2; 2) 2; 3) -2; 24) -4.
84. При каких значениях х являются тождественными следующие равенства 
85. Найдите множество действительных корней уравнения (х 2+1)(х –1) х =0.
86. Найдите множество решений уравнения: (х +1)(х 2+2)+(х +2)(х 2+1)=2.
87. Решите систему уравнений:  .
.
88. Решите неравенство:  < х +5.
< х +5.
89. Решите неравенство относительно переменной х: 2 ах+ 3> a+ 6 х.
90. Найдите множества решений неравенства:  .
.
91. Решите неравенство:  .
.
92. Найдите множество решений системы: 
93. Найдите множество решений совокупности: 
94. Как разрезать параллелограмм на такие две фигуры, из которых можно было бы составить прямоугольник?
95. Известно, что  (b 2)= a 2,
(b 2)= a 2,  (b)= a, b = b 1+ b 2.
(b)= a, b = b 1+ b 2.  (e 1)= k. Найти
(e 1)= k. Найти  (b 1).
(b 1).
1) (а - а 2)· k; 2)  - а 2; 3) а - а 2 k; 4) а 2- аk.
- а 2; 3) а - а 2 k; 4) а 2- аk.
96. Известно, что 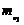 (а)= а 1,
(а)= а 1,  (е 1)= k 1,
(е 1)= k 1,  (e 2)= k 2. Найти
(e 2)= k 2. Найти  (а)
(а)
1) а 1· k 1· k 2; 2) а 1+ k 1+ k 2; 3) а 1· k 2+ k 1; 4) k 2+ a 1 k 1.
97. Выполните с помощью циркуля и линейки основное построение:
«Построение прямой, проходящей через данную точку параллельно данной прямой». Описание построения выполните по шагам, сводя каждый шаг к соответствующему постулату построения.
98. Изобразите многогранник, имеющий 1) 8 ребер; 2) 9 ребер. Проверьте выполнение теоремы Эйлера для этих многогранников.
99. Число граней и их форма у додекаэдра:
1) 8 треугольников; 3) 12 пятиугольников;
2) 6 квадратов; 4) 20 треугольников.
100. Изображением квадрата при параллельном проектировании является:
1) квадрат; 3) параллелограмм;
2) прямоугольник; 4) четырехугольник.
ВАРИАНТ 3
1. Если а и b – различные действительные числа (а < b), то числовое множество  обозначается в виде:
обозначается в виде:
1) [ a,b ]; 2) { a,b }; 3) (a,b ]; 4) (a,b).
2. Множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В, называется:
1) пересечением множеств А и В и обозначается А Ç В;
2) объединением множеств А и В и обозначается А È В;
3) разностью множеств А и В и обозначается А \ В;
4) декартовым произведением двух множеств А и В и обозначается А ´ В.
3. Найдите дополнение множества четных натуральных чисел до множества N 0:
1) множество нечетных натуральных чисел;
2) множество целых чисел;
3) ноль;
4) множество нечетных натуральных чисел и ноль.
4. Запишите для множеств А и В законы двойственности де Моргана.
5. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. Постройте круги Эйлера для данных множеств и отметьте штриховкой область, изображающую множество  \ С.
\ С.
6. У кажите характеристическое свойство элементов множества  , если
, если
K = { x / x Î R, x £ - 2}, L = { x / x Î R, x > 10}.
7. Из 100 школьников 40 играют в футбол, а 50 – в волейбол. Каким может быть число школьников, играющих в обе игры? Хотя бы в одну из игр?
8. Проиллюстрируйте на кругах Эйлера, что для любых множеств А, В и С верно равенство:
(А\В) Ç В=Æ.
9. Изобразите на координатной плоскости А ´ В, если А=(-1;2], В={3,4,8}.
10. Правило произведения в комбинаторике для двух множеств формулируется как:
1) n (А ´ В)= n (A)·(B); 3) n (А Ç В)= n (A) n (B)- n (А È В);
2) n (А È В)= n (A)+ n (B) n (А Ç В); 4) n (А ´ В)= n (A)+ n (B).
11. m! обозначает:
1) произведение всех целых чисел;
2) произведение всех натуральных чисел от 1 до m;
3) сумму всех натуральных чисел от 0 до m;
4) произведение всех неотрицательных целых чисел.
12. Кортеж длины k, составленный из элементов m-элементного множества X, называется:
1) размещениями с повторениями;
2) сочетаниями без повторений;
3) перестановками без повторений;
4) размещениями без повторений.
13. Сколько различных наборов можно составить из 15 различных книг и 4 открыток, если в набор входит одна книга и одна открытка?
1) 15 наборов; 2) 19 наборов; 3) 4 набора; 4) 60 наборов.
14. Размещения c повторениями из m по k вычисляются по формуле:
1) m × k; 3) 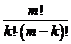 ;
;
2) mk; 4) m (m -1)(m -2)×...×(m - k +1).
15. Сколькими способами можно расставить в ряд на книжной полке 5 книг?
16. Найдите значение выражения:  .
.
17. Вычислите:  .
.
18. Из 60 человек собрание должно выбрать председателя, секретаря и трех членов комиссии. Сколькими способами это можно сделать?
19. Для понятия «параллелограмм» укажите родовое и видовое понятия.
20. Высказывание «А или В» называется:
1) конъюнкцией высказываний А и В;
2) дизъюнкцией высказываний А и В;
3) импликацией высказываний А и В;
4) эквиваленцией высказываний А и В.
21. Конъюнкция двух высказываний А и В истинна тогда и только тогда, когда:
1) А – «И», В – «Л»; 3) А – «И», В – «И»;
2) А – «Л», В – «И»; 4) А – «Л», В – «Л»;
22. Сформулируйте правило силлогизма и приведите пример умозаключения, которое построено по этому правилу.
23. Составьте таблицу истинности для высказывания: ĀÚ(ВÙС).
24. Даны предикаты A(x): «x > 3» и B(x): «x < 4». Найдите множество истинности ТĀÙВ предиката Ā(x)ÙВ(x).
25. Между элементами множеств Х = (2,3,4,5) и Y =(4, 9) задано соответствие Р – число «х является делителем числа y», где х ÎХ, у ÎY. Постройте граф и график соответствия Р.
26. На множестве Х =(3, 5, 7, 9, 11, 13) задано отношение: Р – «меньше». Определите, какими свойствами оно обладает?
1) рефлексивно, симметрично, транзитивно;
2) асимметрично, транзитивно;
3) антисимметрично, транзитивно;
4) рефлексивно, симметрично.
27. Докажите, что множество натуральных чисел равномощно множеству натуральных чисел, кратных 5.
28. Является ли отношение R: «меньше» отношением эквивалентности.
29. В каком случае классификация выполнена верно:
а) натуральные числа делятся на однозначные, двузначные и трехзначные;
б) параллелограммы могут быть прямоугольниками, квадратами и ромбами;
в) треугольники бывают равносторонними и неравносторонними;
г) четырехугольники делятся на параллелограммы и трапеции.
30. Является ли отношение М – «равно» на множестве дробей отношением эквивалентности? На какие классы разбивает это отношение заданное множество дробей?
31. Покажите с помощью графа трактовку системы аксиом Пеано.
32. С помощью метода математической индукции докажите, что для любого целого неотрицательного числа n выражение (10 n +15 n -28) делится на 27.
33. Докажите методом математической индукции, что для любого натурального числа  .
.
34. При делении чисел a, b и c на 8 получаются остатки 3, 4 и 5 соответственно. Какой остаток при делении на 8 дает число a+ b × c?
1) 6; 2) 3; 3) 0; 4) 7.
35. Правило деления числа на произведение.
36. Решите задачу и обоснуйте выбор действий, используя терминологию: а) теоретико-множественную; б) принятую в начальном курсе математики.
В мебельный магазин привезли 500 книжных полок. 30 покупателей купили по 4 полки и 20 покупателей по 8 полок. Сколько полок осталось?
37. Решите различными способами приведенную ниже задачу. Дайте к ней наиболее целесообразную графическую иллюстрацию:
Длина доски 15 м. От нее отрезали 6 м, а оставшийся кусок распилили на 3 равные части. Найдите длину каждой части.
38. Запишите число 11931 в восьмеричной системе счисления:
1) 144678; 2)12568; 3)55628; 4)272338.
39. Запишите число 23445 в двоичной системе счисления:
1) 1010111012; 3) 101101001102;
2) 100000112; 4) 10112.
40. Найдите значение выражения (304357:5427):
1) 367; 2)1237; 3)2637; 4)527.
41. Число тогда и только тогда делится на 4, когда:
1) произведение его цифр делится на 4;
2) сумма его цифр делится на 4;
3) последние две цифры образуют число, делящееся на 4;
4) если оно оканчивается четной цифрой.
42. Не выполняя деления на 45, установите, делится ли на 45 сумма 1872+23152.
43. Докажите, что сумма квадратов трех последовательных натуральных чисел не делится на 3.
44. Числа-близнецы – это:
1) простые числа, разность которых равна 1;
2) составные числа, в написании которых используются одни и те же цифры;
3) простые числа, разность которых равна 2;
4) составные числа, разность которых равна 1.
45. Простых чисел в промежутке от 1 до 100 всего:
1) 25; 2) 11; 3) 15; 4) 13.
46. Каноническим разложением числа 495 является:
1) 22×3×5; 2) 45×11; 3) 32×5×11; 4) 400+95.
47. НОК для чисел 14, 35 и 42 равно:
1) 210; 2) 35; 3) 42; 4) 420.
48. Найдите все числа вида  , делящиеся на 45:
, делящиеся на 45:
1) 13525, 13550; 3) 13505;
2) 13500, 13590, 13545; 4) 0.
49. Что такое «решето Эратосфена»?
50. Определите, какие из чисел 463, 157 и 237 являются простыми, а какие составными?
51. Найдите НОД (а, b) и НОК (а, b) чисел а =299 и b =391, представив их в каноническом виде.
52. Найдите НОД(а, b) чисел а =299 и b =391 с помощью алгоритма Евклида.
53. В три овощных магазина поступили яблоки в одинаковых ящиках. В первый магазин доставили 1800 кг яблок, во второй – 4848 кг, в третий – 2520 кг. Сколько ящиков с яблоками доставили в каждый магазин, если ящики были максимально возможной массы?
54. Изобразить на координатной прямой решение уравнения 
55. Вычислить 3  + 2
+ 2  +
+  .
.
1) 14; 2) 13; 3)  ; 4) 12.
; 4) 12.
56. Решите уравнение  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 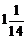 .
.
57. Найдите произведение 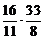 .
.
1) 2; 2) 6; 3) 3; 4) 5.
58. Выполните деление  .
.
1) 6; 2) 10; 3) 4; 4) 8.
59. Найдите значение выражения  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 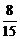 .
.
60. Сократите дробь  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
61. Сравните 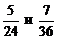 .
.
1) >; 2)<; 3)=; 4)³.
62. Представьте в виде несократимой обыкновенной дроби 7,2(3).
1) 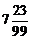 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
63. Сравните 3,272727… и 3,27727772…
1) >; 2) <; 3) =; 4)  .
.
64. Выполните сложение  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
65. Запишите ассоциативный закон сложения положительных рациональных чисел и докажите его.
66. Докажите, что  .
.
67. Расстояние между турбазами А и В равно 40 км. Группа туристов вышла с турбазы А в направлении к турбазе В со скоростью 5 км/ч. Через час с турбазы В навстречу первой группе с той же скоростью вышла другая группа туристов. Через сколько часов после своего выхода вторая группа встретится с первой?
68. Докажите, что если дробь  сократима, то дробь
сократима, то дробь  тоже сократима.
тоже сократима.
69. Найдите пересечение и объединениемножества положительных действительных чисел и множества положительных рациональных чисел.
70. Найдите значение выражения  .
.
71. Каким числом (рациональным или иррациональным) является значение выражения  .
.
72. Найдите приближенное значение суммы х+у, разности х–у, произведения х·у, частного х:у с двумя верными десятичными знаками после запятой, если х=  у =0,28052….
у =0,28052….
73. Вычислите результат с точностью до сотых  .
.
74. Вычислить 
75. Найдите область определения функции y =  .
.
1) (-  ; -5); 3) (-¥; – 5)
; -5); 3) (-¥; – 5)  (-5; +¥);
(-5; +¥);
2) [-5; 5]; 4) (-¥; -5]  (+5; +¥).
(+5; +¥).
76. Укажите число, не принадлежащее области определения функции y =  .
.
1) -1; 2) 0; 3) -7; 4) -2.
77. Найдите область значений функции y =3 cos 2 x.
1) [-2; 2]; 2) [-  ]; 3) [-3, 3]; 4) [
]; 3) [-3, 3]; 4) [ 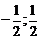 ].
].
78. Выяснить, является ли четной или нечетной функция  :
:
1) является четной;
2) является нечетной;
3) является ни четной, ни нечетной;
4) не является нечетной.
79. Что является графиком данной функции x 2 + у 2–4 х + 4 у = 17.
1) окружность; 2) парабола; 3) гипербола; 4) прямая.
80. Найти интервалы возрастания и убывания функции у = x 2 + 2 х.
81. Укажите множество значений переменной х, при которых выражение имеет смысл 
1) (- 2; 2); 3) (-¥; 2)  (2; +¥);
(2; +¥);
2) [-¥; -2) (-2;2)  (2; +¥); 4) (2; +¥).
(2; +¥); 4) (2; +¥).
82. Решите уравнение 
1) -2; 2) 2; 3) 3; 4) -3.
83. Найти корни уравнения 
1) 2; 2) -2; 3) 4; 4) -4.
84. При каких значениях х являются тождественными следующие равенства 
85. Найдите множество действительных корней уравнения (х 2 – 9)(х –7)(х+ 1) =0.
86. Найдите множество решений уравнения  .
.
87. Решите систему уравнений  .
.
88. Решите неравенство  .
.
89. Решите неравенство относительно переменной х 4 m 2 х+ 4 n 2 х >10.
90. Найдите множество решений неравенства  .
.
91. Решите неравенство 
92. Найдите множество решений неравенств 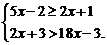
93. Найдите множество решений совокупности 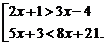
94. Как разрезать прямоугольник на два такие треугольника, из которых можно было бы составить треугольник?
95. Известно, что  (b 1)= a 1,
(b 1)= a 1,  (b 2)= a 2, отрезок b равен сумме отрезков b 1 и b 2,
(b 2)= a 2, отрезок b равен сумме отрезков b 1 и b 2,  (b)= a. Найти
(b)= a. Найти  (е 1).
(е 1).
1) а 1+ а 2; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
96. Известно, что 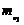 (b 1)= а 1,
(b 1)= а 1,  (b)= а, b = b 1+ b 2
(b)= а, b = b 1+ b 2  (e 1)= k. Найти
(e 1)= k. Найти  (b 2).
(b 2).
1) а – а 1 k; 2) а + а 1 k; 3) а 1– аk; 4) а 1+ аk.
97. Выполните с помощью циркуля и линейки основное построение:
«Деление данного угла пополам». Описание построения выполните по шагам, сводя каждый шаг к соответствующему постулату построения.
98. Какое минимальное число граней может иметь призма? Изобразите такую призму. Проверьте справедливость теоремы Эйлера для этого многогранника.
99. Число граней и их форма у икосаэдра:
1) 12 пятиугольников; 3) 20 треугольников;
2) 8 треугольников; 4) 6 квадратов.
100. Изображением параллелограмма при параллельном проектировании является:
1) четырехугольник 3) прямоугольник;
5) параллелограмм; 4) квадрат.






