Пояснительная записка
В соответствии с реализацией основной образовательной программы бакалаврами I курса педагогического направления (начальное образование) изучаются следующие разделы математики: Аксиоматическое построение множества неотрицательных целых чисел. Теоретико-множественный подход к построению множества неотрицательных целых чисел (количественная теория). Натуральное число как результат измерения величин. Системы счисления. Делимость неотрицательных целых чисел.
Предлагаемые тестовые задания для студентов II курса составлены с учетом того, что одно из наиболее важных умений, которыми должен владеть учащийся начальных классов – это правильно выбирать арифметическое действие при решении задач и обосновывать свой выбор, поэтому будущему учителю необходимы знания теоретических основ выбора действия с использованием аксиоматических и теоретико-множественных понятий.
В связи с вышеизложенным студентам предлагаются задания, учитывающие особенности изучаемых разделов. Поэтому выполнение заданий второй части контрольных материалов сводится не только к записи правильного ответа, но и предполагает анализ и обоснование каждого действия и указанию его теоретической основы.
В работе 23 задания, которые расположены по нарастанию трудности и разделены на 3 части. При этом предполагается проверка как теоретических, так и практических знаний бакалавров по данным темам.
Часть I содержит 12 заданий по определенным разделам математики, которые бакалавры изучают на 2 курсе. К каждому из них приведены 4 варианта ответа, из которых необходимо выбрать один верный.
Часть 2 содержит 10 заданий более высокого уровня сложности, выполнение которых предполагает теоретическое обоснование и подробное описание всех этапов решения.
Часть 3 содержит 3 наиболее сложных задания, для выполнения которых требуется глубокое усвоение изученного материала не только данного раздела, но и ранее изученных тем. При выполнении заданий этой части требуется записать полное решение и теоретическое обоснование этого решения.
Для получения оценки «3» достаточно выполнить верно не менее 10 заданий из всей работы.
Для получения отметки «4» необходимо выполнение не менее 18 заданий из Частей 1 и 2.
Для получения оценки «5» необходимо выполнение заданий Частей 1, 2 и 3. При этом среди верно выполненных заданий должно быть хотя бы одно из Части 3.
За верное выполнение одного задания из Части 1 дается один балл, из Части 2 – два балла, из Части 3 – до 4 баллов. Баллы, полученные за верно выполненные задания, суммируются.
Вариант тестовых заданий и контрольных материалов по Модулю II
(по темам: Системы счисления. Делимость неотрицательных целых чисел)
Часть 1
А1. При делении чисел a, b и с на 7 получаются остатки 1, 4 и 5 соответственно. Какой остаток при делении на 7 дает число a + b + c?
1) 6; 2) 3; 3) 0; 4) 7.
А2. Запишите число 6455 в восьмеричной системе счислений:
1) 144678; 2) 12568; 3) 55628; 4) 272338.
А3. Запишите число 18769 в двоичной системе счисления:
1) 10001012; 2) 100000112;
3) 101101001102; 4) 10112.
А4. Найдите значение выражения (412136: 456):
1) 5136; 2) 1236; 3) 236; 4) 5026.
А5. Число тогда и только тогда делится на 9, когда:
1) произведение его цифр делится на 9;
2) сумма его цифр делится на 9;
3) последние две цифры образуют число, делящееся на 9;
4) если оно оканчивается нечетной цифрой.
А6. Множество N 0 разбивается на попарно непересекающиеся подмножества:
1) числа простые и составные;
2) числа простые, составные и 0;
3) простые, составные и 1;
4) простые, составные, 1 и 0.
А7. Простых чисел в промежутке от 1 до 35 всего:
1) 25; 2) 11; 3) 12; 4) 13.
А8. Каноническим разложением числа 84 является:
1) 23 × 3 × 7; 2) 4 × 21;
3) 22 × 3 × 7; 4) 2 × 42.
А9. НОК для чисел 5, 14 и 35 равно:
1) 70; 2) 35; 3) 140; 4) 210.
А10. Найдите все числа вида  , делящиеся на 25:
, делящиеся на 25:
1) 51730, 51710, 51780; 2) 517700;
3) 25; 4) 51700, 51725, 51750, 51775.
Часть 2
В1. Перечислите свойства множества целых неотрицательных чисел N 0.
В2. С помощью метода математической индукции докажите, что для любого целого неотрицательного числа n выражение (4 n + 15 n – 1) делится на 9.
В3. Правила деления суммы на число и разности на число.
В4. Докажите методом математической индукции, что для любого натурального числа  .
.
В5. Решите задачу и обоснуйте выбор действия, используя терминологии: а) теоретико-множественную; б) принятую в начальном курсе математики.
Для школьного сада привезли 24 саженца яблонь и 6 саженцев груш. Их посадили поровну в 6 рядов. Сколько саженцев посадили в каждом ряду?
В6. В чем заключается алгоритм Евклида?
В7. Определите, какие из чисел 471, 247 и 253 является простыми, а какие составными?
В8. Найдите НОД (а, b) и НОК (а, b) чисел а = 548 и b = 2466, представив в каноническом виде.
В9. Найдите НОД (а, b) чисел а = 548 и b = 2466 с помощью алгоритма Евклида.
В10. На новогодней елке ребята получили одинаковые подарки. Во всех подарках было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке?
Часть 3
С1. Решите различными способами приведенную ниже задачу. Дайте к ней наиболее целесообразную графическую иллюстрацию:
Мост через реку имеет три пролета. Длина первого пролета 24 м. Третий пролет на 12 м первого, а второй на 7 метров короче первого. Найдите длину моста.
С2. Не выполняя сложения, установите, делится ли на 36 сумма: 1872 + 23152.
С3. Докажите, что разность квадратов двух последовательных натуральных чисел есть число нечетное.
Вариант тестовых заданий и контрольных материалов по Модулю III
(по темам: Расширение понятия числа. Действительные числа)
Часть 1
А1. Вычислить  .
.
1)  ; 2)
; 2) 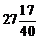 ; 3)
; 3)  ; 4)
; 4)  .
.
А2. Решите уравнение 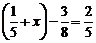 .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
А3. Найдите произведение  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 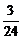 .
.
А4. Выполните деление  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 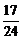 .
.
А5. Найдите значение выражения  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
А6. Сократите дробь  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
А7. Сравните  и
и 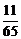 .
.
1) >; 2) <; 3) =.
А8. Представьте в виде несократимой обыкновенной дроби 6,2(7).
1) 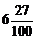 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
А9. Сравните  и
и  .
.
1) >; 2) <; 3) =.
А10. Выполните сложение  .
.
1)  ; 2)
; 2) 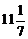 ; 3)
; 3)  ; 4)
; 4)  .
.
Часть 2
В1. Запишите коммутативный закон сложения положительных рациональных чисел и докажите его.
В2. Докажите, что 

В3. В трех цехах завода работает 2740 человек. во втором цехе работает на 140 человек больше, чем в первом, а в третьем цехе – в 1,2 раза больше во втором. Сколько человек работает в каждом цехе?
В4. Найдите пересечение и объединение множества натуральных чисел и множества положительных действительных чисел.
В5. Найдите значение выражения  .
.
В6. Каким числом (рациональным или иррациональным) является значение выражения  .
.
В7. Найдите приближенное значение суммы x + y, разности x – y, произведения x × y, частного x: y, с двумя верными десятичными знаками после запятой, если x = 0,666…, у = 0,57079 …
В8. Вычислите результат с точностью до сотых  .
.
В9. Изобразить на координатной прямой решение уравнения  .
.
Часть 3
С1. Вычислить  .
.
С2. Докажите, что если дробь  сократима, то дробь
сократима, то дробь 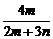 тоже сократима.
тоже сократима.
Вариант тестовых заданий по Модулю IV
(по темам: Числовые функции. Уравнения и неравенства)
Часть 1
А1. Найдите область определения функции  .
.
1)  ; 2) [0; +¥); 3)
; 2) [0; +¥); 3)  ; 4) [1; +¥).
; 4) [1; +¥).
А2. Укажите число, принадлежащее области определения функции  .
.
1) 44; 2) 5; 3) -5; 4) 1.
А3. Найдите область значений функции  .
.
1) [2; 6]; 2) [-12; 12]; 3) [-6; 6]; 4) [6; 2].
А4. Выяснить, является ли четной или нечетной функция 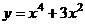 .
.
1) является четной;
2) является нечетной;
3) является ни четной, ни нечетной.
А5. Что является графиком данной функции  .
.
1) окружность; 2) парабола;
3) гипербола; 4) прямая.
А6. Между какими целыми числами заключено число  .
.
1) 2 и 3; 2) 3 и 4; 3) 4 и 5; 4) 9 и 11.
А7. Расставьте скобки в выражении 56 – 24: 2 + 6 так, чтобы его значение было ровно 50.
1) (56 – 24): 2 + 6; 2) 56 – 24: (2 + 6);
3) 56 – (24: 2)+ 6; 4) (56 – 24): (2 + 6).
А8. Укажите множество значений переменной х, при которых выражение имеет смысл 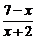 .
.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
А9. Решите уравнение 3 х + 7 = 2 х – 4.
1) –9; 2) –11; 3) –13; 4) 11.
А10. Найдите корни уравнения  .
.
1) 4; 2) –4; 3) –4; 4; 4) 2.
Часть 2
В1. Найти интервалы возрастания и убывания функции  .
.
В2. Сравните значения числовых выражений  и
и  .
.
В3. При каких значениях х является тождествами следующие равенства
 .
.
В4. Найдите множество действительных корней уравнения  .
.
В5. Решите систему уравнений  .
.
В6. Решите задачу составлением уравнения.
Бригада должна выполнить заказ за 12 дней. Ежедневно перевыполняя норму на 25% за 10 дней работы она не только выполнила заказ, но еще и изготовила сверх нормы 42 детали. Сколько деталей в день изготовила бригада?
В7. Решите неравенство  .
.
В8. Решите неравенство относительно переменной х  .
.
В10. Решите неравенство  .
.
Часть 3
С1. Найдите множество решений уравнения  .
.
С2. Найдите множество решений системы неравенств  .
.
С3. Найдите множество решений совокупности 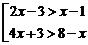 .
.
Вариант тестовых заданий по по Модулям V и VI
(по темам: Величины и их измерение. Различные подходы к введению аддитивно-скалярных величин. Величины, изучаемые в начальной коле. Единицы измерения величин)
Часть 1
А1. Известно, что  . Отрезок a = b + c. Найти
. Отрезок a = b + c. Найти  .
.
1) 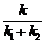 ; 2)
; 2) 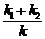 .
.
А2. Известно, что  . Найти
. Найти  .
.
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
А3. Число граней и их форма у октаэдра:
1) 12 пятиугольников; 2) 6 квадратов; 3) 8 треугольников.
А4. Изображением правильного треугольника при параллельном проектировании является:
1) правильный треугольник;
2) произвольный треугольник;
3) равнобедренный треугольник.
Часть 2
В1. Выполните с помощью циркуля и линейки основное построение:
«Построение угла, равного данному». Описание построения выполните по шагам, сводя каждый шаг к соответствующему постулату построения.
В2. Изобразите и назовите многогранник, имеющий наименьшее число граней. Сколько у него ребер, вершин, диагоналей? Проверьте выполнение теоремы для этого многогранника.
Часть 3
С1. С помощью циркуля и линейки решите задачу на построение:
Постройте треугольник по стороне, медиане, проведенной к этой стороне и радиусу описанной окружности.
С2. Дано изображение окружности. Построить изображение правильного треугольника:
1) вписанного в данную окружность;
2) описанного около него.






