Студенты должны знать:
· определения и свойства теоретико-множественных операций и отношений, определение разбиения множества на классы;
· основные правила и методы решения комбинаторных задач;
· основные способы определения понятия, виды определений, требования к определению;
· простейшие схемы правильных рассуждений;
· теоретико-множественное обоснование арифметики целых неотрицательных чисел;
· основы аксиоматического метода, аксиоматическое обоснование арифметики целых неотрицательных чисел;
· основы построения непозиционных и позиционных систем счисления, алгоритмы действий в десятичной системе счисления, принципы работы ЭВМ;
· определение и свойства отношения делимости, основные признаки делимости;
· определение рационального числа и операций с рациональными числами, законы сложения и умножения, свойства множества рациональных чисел;
· определение операций с действительными числами, законы сложения и умножения;
· определение уравнения и неравенства с одной переменной;
· определение геометрических преобразований;
· важнейшие величины, изучаемые в начальном курсе математики.
Студенты должны овладеть следующими математическими компетенциями:
· выполнять теоретико-множественные операции над конечными и бесконечными множествами, в том числе и над геометрическими фигурами;
· устанавливать способ задания конкретного отношения и формулировать его свойства;
· распознавать числовые функции, устанавливать наличие прямой и обратной пропорциональности;
· находить ошибки в рассуждениях;
· иллюстрировать теоретико-множественный подход к числу и операциям над числовыми примерами из учебников математики для начальных классов, обосновывать выбор действия при решении простых текстовых задач;
· иллюстрировать аксиоматический подход примерами из начального курса математики;
· применять признаки делимости на практике, находить наибольший общий делитель и наименьшее общее кратное, устанавливать делимость суммы, разности и произведения на данное число, не выполняя указанных действий над числами;
· выполнять вычисления с рациональными числами;
· решать геометрические задачи на вычисление, доказательство, построение;
· практически измерять величины: длину, площадь, объем, время, массу и др.;
· устанавливать вид зависимости между величинами при решении текстовых задач;
· решать простейшие комбинаторные задачи;
· анализировать структуру определений понятий;
· анализировать простейшие рассуждения;
· решать и обосновывать решения уравнений и неравенств с одной переменной;
· решать и обосновывать решения задач на геометрическое преобразование фигур;
· изображать фигуры на плоскости.
3.5. МАТЕРИАЛЫ ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНЫХ И ИТОГОВЫХ АТТЕСТАЦИЙ
по математике для студентов дневного отделения с 1 по 3 курс
(всего 5 типов контрольных заданий)
для бакалавров I курса педагогического направления. Начальное образование
Пояснительная записка
Предлагаемые ниже тестовые задания предназначены для бакалавров I курса по направлению подготовки 050100 Педагогическое образование. Начальное образование. Тестовые задания составлены для каждого из разделов, изучаемых бакалаврами на I курсе в соответствии с требованиями обязательными при реализации основной образовательной программы подготовки.
В работе 28 заданий, которые расположены по нарастанию трудности и разделены на 3 части. При этом предполагается проверка как теоретических знаний и компетенций студентов по данным темам.
Часть I содержит 12 заданий по определенным разделам математики. К каждому из них приведены 4 варианта ответа, из которых необходимо выбрать один верный.
Часть 2 содержит 12 заданий более высокого уровня сложности. При выполнении заданий этой части необходимо записать только полученный ответ.
Часть 3 содержит 4 наиболее сложных заданий, для выполнения которых требуется глубокое усвоение изученного материала на уровне компетенций. При выполнении заданий этой части требуется записать полное решение и теоретическое обоснование этого решения.
Для получения оценки «3» достаточно выполнить верно не менее 10 заданий из всей работы.
Для получения отметки «4» необходимо выполнение не менее 22 заданий из Частей 1 и 2.
Для получения оценки «5» необходимо выполнение заданий Частей 1,2 и 3. При этом среди верно выполненных заданий должно быть хотя бы одно из Части 3.
За верное выполнение одного задания из Части 1 дается один балл, из Части 2 – два балла, из Части 3 – до 4 баллов. Баллы, полученные за верно выполненные задания, суммируются.
Вариант тестовых заданий по Модулю I
(по темам: Множества и операции над ними. Элементы комбинаторики.
Математические утверждения и их структура)
Часть 1
А1. Множество, состоящее из всех элементов, принадлежащих и множеству А и множеству В одновременно, называется:
1) пересечением множеств А и В и обозначается  ;
;
2) объединением множеств А и В и обозначается  ;
;
3) разностью множеств А и В и обозначается  ;
;
4) декартовым произведением двух множеств А и В обозначается  .
.
А2. Если а и b – различные действительные числа (a < b), то числовое множество  обозначается в виде:
обозначается в виде:
1) [ a, b ]; 2) { a, b }; 3) (a, b); 4) (-¥, +¥).
А3. Укажите множество А = В / С, которое является разностью множеств В = {10, 12, 16, 19, 21} и С = {10, 16, 21}:
1) А = {10, 12, 16, 19, 21}; 2) А = {12, 19};
3) А = {10, 16, 21}; 4) A = Æ.
А4. Если отношение R на множестве Х транзитивно и ассиметрично, то R является отношением:
1) строгого порядка; 2) эквивалентности;
3) нестрогого порядка; 4) биективным.
А5. В каком случае классификация выполнена верно:
1) множество всех треугольников можно разбить на остроугольные, тупоугольные и прямоугольные;
2) множество всех треугольников можно разбить на классы равнобедренных, равносторонних и разносторонних треугольников;
3) натуральные числа делятся на однозначные, двузначные и трехзначные;
4) параллелограммы могут быть прямоугольниками, квадратами и ромбами.
А6. Правило суммы в комбинаторике для двух непересекающихся множеств формулируется как:
1) 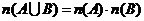 ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 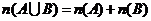 .
.
А7.  обозначает:
обозначает:
1) произведение всех целых чисел;
2) произведение всех натуральных чисел от 1 до m;
3) сумму всех натуральных чисел от 0 до m;
4) произведение всех неотрицательных целых чисел.
А8. Упорядоченные k -элементные множества, составленные из элементов m-элементного множества Х, называются:
1) размещениями с повторениями;
2) размещениями без повторения;
3) перестановками без повторений;
4) размещениями без повторения.
А9. На тарелке лежат 5 яблок и 4 груши. Сколькими способами можно выбрать один плод?
1) 14 способами; 2) 9 способами;
3) 5 способами; 4) 4 способами.
А10. Сочетания без повторения из m по k вычисляются по формуле:
1)  ; 2) mk; 3)
; 2) mk; 3)  ; 4)
; 4)  .
.
А11. Высказывание «если А, то В» называется:
1) конъюнкцией высказываний А и В;
2) дизъюнкцией высказываний А и В;
3) импликацией высказываний А и В;
4) эквиваленцией высказываний А и В.
А12. Дизъюнкция двух высказываний А и В ложна тогда и только тогда, когда:
1) А – «И», В – «Л»; 2) А – «Л», В – «И»;
3) А – «И», В – «И»; 4) А – «Л», В – «Л».
Часть 2
В1. Запишите для множеств А, В и С свойство ассоциативности пересечения.
В2. А – множество прямоугольников, В – множество правильных многоугольников, С – множество треугольников. Постройте круги Эйлера для данных множеств и отметьте штриховкой область, изображающую множество 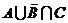 .
.
В3. Укажите характеристическое свойство элементов множества  , если
, если 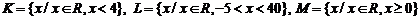 .
.
В4. Отношение Т: «Число х делится на число y» задано на множестве А = {1, 2, 6, 8}. Постройте граф и график отношения Т, определите его свойства.
В5. Изобразите на координатной плоскости  , если А = (-3; 3], B = (1; 3).
, если А = (-3; 3], B = (1; 3).
В6. Из 80 школьников 40 играют в футбол, а 50 – в волейбол. Каким может быть число школьников, играющих в обе игры? Хотя бы в одну из игр?
В7. Сколькими способами из 10 человек можно выбрать комиссию, состоящую из 3 человек?
В8. Найдите значение выражения:  .
.
В9. Вычислите: 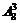 .
.
В10. Даны предикаты А (х): «x > 3» и В (x): «x < 4». Найдите множество истинности  предиката
предиката  .
.
В11. Перечислите свойства, входящие в содержание понятия «прямоугольник».
В12. Сформулируйте правило заключения и приведите пример умозаключения, которое построено по этому правилу.
Часть 3
С1. Докажите, что для любых множеств А и В верно равенство  .
.
С2. Докажите, что множество натуральных чисел равномощно множеству нечетных натуральных чисел.
С3. Сколько пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4 при условии, что каждая цифра входит в пятизначное число только один раз?
С4. Составьте таблицу истинности для высказывания:  .
.






