Элементы математической статистики

   Методы математической статистики позволяют систематизировать и оценивать экспериментальные данные, которые рассматриваются как случайные величины.

Методы математической статистики нашли широкое применение при обработке данных медико-биолоических исследований. В биологических и медицинских исследованиях приходится иметь дело с очень сложными опытами, в которых многие факторы не поддаются строгому учету и контролю. Для определения значения конкретного параметра, свойственного организму в том или ином состоянии, необходим анализ достаточно большого числа случаев (тысяч) обследования соответствующих пациентов. Однако математическая статистика позволяет даже при небольшом числе пациентов составить конечную выборку значений функционального параметра и приближенно рассчитать её основные характеристики: среднюю конечных выборок, среднее квадратическое отклонение, а также определить доверительные границы генеральной средней.

Цель занятия:

1. Научться строить гистограммы и полигоны для случайных величин.
2. Находить границы доверительного интервала для оценки математического ожидания нормального распределения

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ. ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ

       Математическая статистика – наука о математических методах систематизации и использования статистических данных для решения научных и прикладных задач.

       Математическая статистика тесно примыкает к теории вероятностей и базируется на её понятиях. Однако главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют.

       Наиболее общая совокупность, состоящая из всех объектов, которые могут быть к ней отнесены называется генеральной совокупностью. Её изучение трудно, поэтому вводится понятие выборочной совокупности или просто выборки. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.

       Свойства объектов выборки должно соответствовать свойствам генеральной совокупности, т.е. выборка должна быть репрезентативной (или представительной). При этом выборка должна осуществляться случайно. Например, изучается состояние здоровья населения большого города. При этом нельзя воспользоваться выборкой населения одного района города, так как условия проживания в разных районах могут отличаться и таким образом влиять на состояние здоровья. Поэтому выборка должна представлять случайно отобранные объекты всего города.

2. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ

       Если записать в последовательности измерений все значения величины х в выборке, то получим простой статистический ряд. Такой ряд неудобен для анализа, так как в нем нет последовательности возрастания (или убывания) значений, встречаются и повторяющиеся величины.

       Пусть n – это объем выборки.

Признак х₁ появился m ₁ раз

х₂ появился m ₂ раз

           ……………………

x_k появился m_k раз

Значения признака х₁, х₂, …, х _k – это варианты.

       Последовательность вариант, записанных в возрастающем порядке называется вариационным (или ранжированным) рядом.

m ₁, m ₂,..., m_k – это частоты появления признака

 - это относительные частоты появления признака или вероятности:

…,

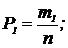
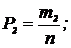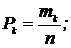
Причем:

       Дискретный вариационный ряд представляют в виде таблицы, которая называется статистическим дискретным рядом распределения.

х	х1	х2	…	xi	…	xk
m	m1	m2	…	mi	…	mk
			…		…

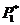
       В этом случае строится полигон: по оси абцисс откладывают значения вариант х _i а по оси ординат – значения частот m_i (или относительных частот ). Строится ломанная, которая называется полигоном частот (или относительных частот):

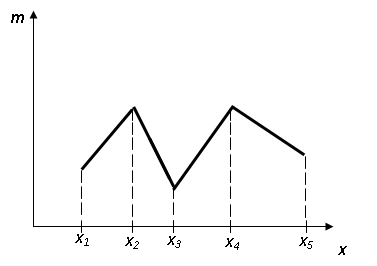
Полигон частот

 

Непрерывный вариационный ряд представляют в виде таблицы, которая называется статистическим интервальным рядом распределения.

Интервал	х0- х1	х1-х2	…	xi-1-xi	…	xk-1-xk
m	m1	m2	…	mi	…	mk
			…		…

           

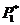
В этом случае строится гистограмма. По оси абцисс откладываются интервалы длиной Δх (Δх – шаг интервала, определяется разностью между максимальным и минимальным значением интервала) и на каждом интервале строят прямоугольник с основанием Δх и высотой   (или ).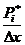

       Частоту (или относительную частоту), приходящуюся на единицу интервала называют плотностью частоты (или относительной частоты).

       При увеличении числа наблюдений и уменьшении длины (Δх) интервалов верхняя ступенчатая линия гистограммы будет стремиться к плавной кривой и в пределе эта кривая будет графиком плотности вероятности.

           

3. СРЕДНИЕ ЗНАЧЕНИЯ ВЕЛИЧИН И СПОСОБЫ ИХ ОПРЕДЕЛНИЯ

       При обработке результатов экспериментальных наблюдений большое значение имеют средние величины.