Задача 1. Значения вязкости крови принимали следующие значения:
| Вязкость крови xi (Па∙с∙10-3) | 4,2 | 3,8 | 5,0 | 5,3 | 6,1 | 4,0 | 4,5 | 5,2 | 5,8 | 3,5 |
| Количество пациентов mi | 18 | 12 | 21 | 9 | 2 | 28 | 31 | 8 | 7 | 4 |
Вычислить выборочную среднюю арифметическую, медиану и моду. Построить полигон частот.
Задача 2. Показания веса детей в возрасте полутора лет представлены в таблице
| Вес детей, xi (кг) | 8,5-9,0 | 9,0-9,5 | 9,5-10,0 | 10,0-10,5 | 10,5-11 | 11-11,5 | 11,5-12 | 12-12,5 |
| Количество детей mi | 77 | 23 | 16 | 13 | 21 | 51 | 9 | 10 |
Вычислить выборочную среднюю арифметическую, медиану и моду. Построить гистограмму.
Задача 3. Найти исправленную дисперсию S 2 иcтандарт отклонения S для общего белка крови, данные которого представлены в таблице:
| Общий белок крови, xi (г,%) | 6,81 | 5,90 | 7,04 | 6,72 | 6,54 | 6,89 | 5,54 |
| Количество пациентов mi | 14 | 8 | 7 | 21 | 15 | 10 | 5 |
Задача 4. Найти исправленную дисперсию S 2 стандарт отклонения S для:
- Общего белка крови
| xi | 7,3 | 7,2 | 7,1 | 7,0 | 6,9 | 6,8 | 6,7 | 6,6 | 6,5 | 6,4 |
| mi | 1 | 2 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | 1 |
2. Свободного гепарина крови
| xi (мг%) | 5,7 | 5,9 | 6,3 | 6,6 | 5,0 | 3,7 | 4,0 | 4,5 | 5,0 | 5,6 |
| mi | 4 | 3 | 2 | 1 | 10 | 2 | 2 | 4 | 3 | 4 |
- Веса щитовидной железы
| xi (г) | 60 | 68 | 70 | 72 | 90 | 100 | 105 | 120 | 125 | 130 |
| mi | 2 | 2 | 6 | 5 | 7 | 8 | 7 | 2 | 3 | 4 |
Задача 5. Значения скорости секреции альдестерона (мкг/сутки) при ожирении имели следующие величины:
370 274 337 326 281 349 403 350 315 358
Определить среднее арифметическое и величину доверительного интервала при доверительной вероятности Р=0,95.
Задачи для решения на практическом занятии:
Задача 1. У обследуемых пациентов нижняя граница артериального давления оказалось равной:
| Нижняя граница артериального давления xi (мм.рт.ст) | 67 | 80 | 110 | 74 | 85 | 100 | 90 | 105 | 78 | 64 |
| Количество пациентов mi | 5 | 18 | 7 | 24 | 16 | 9 | 11 | 2 | 14 | 4 |
Вычислить выборочную среднюю арифметическую, медиану и моду.
Задача 2. Найти исправленную дисперсию S 2 cтандарт отклонения S для объема циркулирующей крови:
| Объем циркулирующей крови xi (л) | 4,3 | 5,1 | 4,8 | 5,5 | 4,7 | 6,0 | 5,3 |
| Количество пациентов mi | 8 | 21 | 11 | 13 | 27 | 2 | 18 |
Задача 3. Содержание норадреналина в моче при грудной жабе имели следующие значения:
36,9 38,2 36,1 33,5 34,8 37,0 35,1 40,0 38,5 36,3
Определить среднее арифметическое и величину (границы) доверительного интервала при доверительной вероятности Р=0,99.
Задача 4. У животных летальные дозы препарата А составляют
1,55; 1,58; 1,71; 1,44; 1,24; 1,89; 2,34.
Найти среднее арифметическое и величину доверительного интервала при доверительной вероятность 0,95.
Задача 5. Десять измерений общего белка крови (г%) при гепатите дали следующие результаты:
7,2; 6,92; 7,03; 7,52; 7,48; 7,1; 7,25; 7,18; 7,05; 7,00
Найти среднее арифметическое и величину доверительного интервала (при доверительной вероятность 0,95).
ТЕМА №10
ТЕОРИЯ КОРРЕЛЯЦИИ
Выявление связей (корреляций) между различными случайными параметрами и случайными процессами широко используется в медицинской диагностике. С помощью корреляционного анализа решаются задачи установления обоснованного диагноза. Целью диагноза является установление с высокой надежностью вида заболевания при определенных симптомах. Установление корреляций между различными показателями состояния больного и влиянием их изменений на жизнедеятельность организма является важной задачей лабораторных и клинических исследований.
Все системы, ткани, органы, клетки организма находятся в корреляционной связи друг с другом.
Определение коэффициента корреляции позволяется определить существование и степень связи между различными выборками.
Цель занятия:
· Научиться определять величину коэффициента корреляции.
· Определять вид и степень связи между выборками по величине и знаку коэффициента корреляции.
· Научиться строить корреляционное поле и проводить линию регрессии.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. ФУНКЦИОНАЛЬНАЯ, СТАТИСТИЧЕСКАЯ И КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТИ
Две случайные величины могут быть связаны функциональной зависимостью, быть независимыми, либо статистически зависимыми.
Если значению одной величины соответствует строго определенное значение другой величины, то зависимость между ними называется функциональной. Функционально связанные случайные величины х и у могут принимать различные значения, но если х приняла определенное значение, то у соответствует ему однозначно.
Статистической зависимостью величины у от величины х называется зависимость при которой каждому значению величины х из множества её возможных значений соответствует некоторое множество возможных значений величины у, характеризуемое определенным законом распределения.
Частным случаем статистической зависимости является корреляционная (или стохастическая). Понятие корреляции соответствует русскому термину «соотношение».
Основные регулирующие системы организма непрерывно осуществляют стабилизацию всех параметров. При возникновении патологии (или при изменении внешних воздействий) изменение значения одного параметра влечет за собой изменения в различной степени значений других параметров. В силу наличия обратных связей и множественности путей саморегуляции организма связь между его параметрами является случайной и может быть описана не функциональной зависимостью, а корреляционной связью. Выявление связей (корреляций) между различными случайными параметрами и случайными процессами широко используется в медицинской диагностике.
Благодаря различным формам корреляции (физико-химическим, нервным, морфофизиологическим, эволюционным и т.д.) организм проявляется как единая сложная целостная система.
Корреляция обозначает главным образом степень выраженности связи между вариационными рядами. Например, между массой тела человека и объемом циркулирующей крови, между основным обменом веществ и амплитудной артериального давления. Уже в 1637 г. Галилей обсуждал связь между размерами скелета и массой организма.
2. КОРРЕЛЯЦИОННОЕ ПОЛЕ, ЛИНИИ И УРАВНЕНИЯ РЕГРЕССИИ
Наглядно корреляционная зависимость может быть выражена графически. На осях абцисс и ординат откладываются значения вариационных рядов. Для каждого отдельного наблюдения получают значения в каждом из вариационных рядов. Эти значения (при данном наблюдении) соответствуют друг другу и их совокупность обозначается точкой на плоскости. Число таких точек оказывается равным числу наблюдений. Совокупность точек на плоскости называется корреляционным полем, оно создаёт общую картину корреляции и обычно позволяет построить усреднённую кривую – линию регрессии – взаимосвязи параметров, составляющих два вариационных ряда.
Если между величинами существует связь, то корреляционное поле имеет вид элипса со сгущениям точек вокруг главной оси и их малым числом на периферии (рис. 1).
Рис 1. Линия регресии rx , y >0, Рис 2. Отсутствие корреляционной связи rx , y =0
Если связь выражена слабо, то разброс точек велик (рис. 2).
При корреляционной зависимости изменение одной из величин влечет изменение математического ожидания другой. Эту зависимость можно записать в помощью уравнения вида:
- уравнение регрессии у на х.
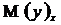- это условное математическое ожидание величины у, соответствующее данному значению х.
х - отдельные значения величины х.
f (x) -некоторая функция
- уравнение регрессии х на у.
Функции f (x) и f (у) называют регрессиями у на х и х на у соответственно. Графики этих функций называются линиями регрессии.
Корреляционная зависимость может быть линейной, квадратической, экспоненциальной и т.д.
Если f (x) и f (у) – линейные функции, то уравнения регрессии имеют вид:
где А, В, С, Д – это некоторое параметры. Для определения этих параметров применяют метод наименьших квадратов (рассматривать не будем).
3. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ И ЕГО СВОЙСТВА
Мера зависимости между вариационными рядами характеризуется коэффициентом корреляции. Для линейной корреляционной зависимости угловые коэффициенты прямых регрессии выражаются через коэффициент корреляции, который определяется по формуле Пирсона:
,
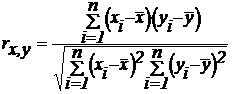где 
- коэффициент корреляции
х i, yi – значения параметров в i -том наблюдении
n – число наблюдений
- средние значения параметров х и у для n проведённых
наблюдений.
или:
где 
- генеральные средние квадратические отклонения,
k х,у - называется корреляционным моментом или ковариацией.
Коэффициент корреляции показывает долю рассеяния величины х под влиянием у (и наоборот).
4. СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Величина коэффициента корреляции всегда заключена в пределах:
1. Если r <0, то с увеличением в вариационном ряду наблюдаемых значений х соответствующие им значения у вариационного ряда уменьшаются.
2. Если r >0, то с увеличением одного параметра другой параметр в среднем возрастает.
3. Если r =0, то параметры х и у абсолютно независимы друг от друга.
4. Если r =1, то между параметрами х и у существует прямо пропорциональная функциональная зависимость.
5. Чем больше по абсолютной величине , тем сильнее проявляется связь между х и у, тем ближе эта зависимость к функциональной и тем значительнее влияние х ( или у ) на у (или х) среди всех других влияющих факторов.
6. Чем больше абсолютная величина , тем больше доверительная вероятность того, что характер этой связи действительно соответствует полученному коэффициентному корреляции.
Принято считать, что связь между исследуемыми параметрами или явлениями:
а) слабая при 
б) средняя при 
в) тесная при 
5. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ ЛИНЕЙНОЙЗАВИСИМОСТИ
Для экспериментального изучения зависимости между двумя величинами х и у производят некоторое количество n независимых испытаний:
х1, х2,...,х n
y 1, y 2,..., yn
Результат i -того измерения дает пару значений xi, yi ( i =1,2,….. n).
Вычисления производят в следующем порядке:
- Вычисляют выборочные средние:
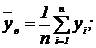
- Вычисляют выборочные средниеквадратические отклонения:
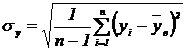
- Вычисляют оценку ковариации.
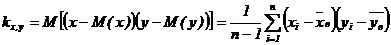
- Вычисляют коэффициент корреляции
