Задача 1. Содержание свободного гепарина крови принимало следующие значения хi с частотой появления mi.
| хi(мг,%) | 5,7 | 5,9 | 6,3 | 5,6 | 4,1 | 4,0 | 4,5 | 5,0 | 5,1 | 6,7 |
| mi | 5 | 11 | 2 | 7 | 4 | 15 | 13 | 23 | 9 | 1 |
Вычислить выборочную среднюю арифметическую, медиану и моду. Построить полигон частот.
Решение:
Выборочная средняя определяется по формуле:
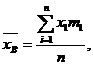
где 
-сумма произведений значений выборки х i на соответствующую частоту их появлений mi,
n -объем выборки, определяемой через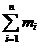 
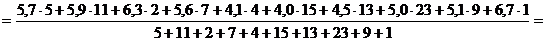
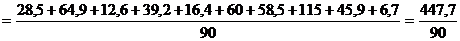=4,974≈4,97 (мг,%)
Для определения медианы по заданным параметрам х i строим вариационный ряд:
| хi | 4,0 | 4,1 | 4,5 | 5,0 | 5,1 | 5,6 | 5,7 | 5,9 | 6,3 | 6,7 |
| mi | 15 | 4 | 13 | 23 | 9 | 7 | 5 | 11 | 2 | 1 |
При четном числе вариант медиана определится как среднее арифметическое из двух центральных вариант
(мг,%)
Мода:
М0 =5,0 (мг,%)
Используя данные таблицы, строим полигон частот:
Ответ: 
=4,97 мг,% Ме=5,0 (мг,%) М0=5,0 (мг,%)
Задача 2. Измерения роста девочек в возрасте от трех до 5 лет представлены в виде статистического интервального ряда распределения:
| Рост в см (хi) | 92-95 | 95-98 | 98-101 | 101-104 | 104-107 | 107-110 | 110-113 |
| Количество девочек mi | 5 | 17 | 23 | 31 | 45 | 19 | 20 |
Вычислить выборочную среднюю арифметическую. Построить гистограмму.
Решение:
Выборочную среднюю арифметческую находим по формуле:
= 
,
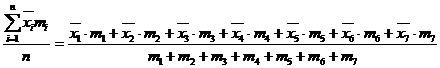где 
(см)
(см)
(см)
(см)
(см)
(см)
(см)
Вычисляем :
(см)
Для построение гистограммы определяем шаг (ширину) интервала:
D х =95-92=3 (см)
Определяем отношения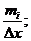 
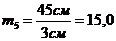
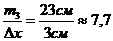
Строим гистограмму:
Ответ: 
=103,8см.
Задача 3. Измерение веса девочек xi в возрасте 10 лет дало следующие результат:
| xi (кг) | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| mi | 2 | 1 | 6 | 8 | 21 | 20 | 18 | 12 | 3 | 4 | 2 | 3 |
Построить полигон частот. Вычислить выборочную среднюю арифметическую, медиану и моду.
Решение
Построим полигон частот:
Выборочная средняя арифметическая будет:
Медиана: Ме =24,5 кг
Мода: Мо =23 кг
Задача4. Измерения роста мужчин представлены статистическим интервальным рядом распределения:
| xi (см) | 150-154 | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 | 182-186 |
| mi | 1 | 3 | 11 | 23 | 25 | 22 | 11 | 3 | 1 |
Построить гистограмму. Вычислить выборочное среднее арифметическое, медиану и моду.
Решение
Находим шаг интервала ∆х:
∆х =154-150=4 (см)
Заполняем таблицу:
| xi (см) | 150-154 | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 | 182-186 |
| mi | 1 | 3 | 11 | 23 | 25 | 22 | 11 | 3 | 1 |
| 154 | 156 | 160 | 164 | 168 | 172 | 176 | 180 | 184 |
| 152 | 468 | 1760 | 3772 | 4200 | 3784 | 1936 | 540 | 184 |
| 0,25 | 0,75 | 2,75 | 5,75 | 6,25 | 5,5 | 2,75 | 0,75 | 0,25 |
Медиана: 
Мода: Мо =168см
Задача 5. Найти исправленную дисперсию S 2,стандарт отклонения S для показателя гемоглобина, значения которого приведены ниже.
| Показатель гемоглобина xi | 73 | 72 | 71 | 70 | 69 | 68 | 67 | 66 | 65 | |
| Число лиц mi | 2 | 4 | 6 | 10 | 11 | 7 | 5 | 4 | 1 | n=50 |
Решение
Составим дополнительную таблицу:
| xi mi | 146 | 288 | 426 | 700 | 759 | 476 | 335 | 264 | 65 | 
|
| 14,59 | 7,95 | 3,3 | 0,67 | 0,32 | 1,39 | 4,75 | 10,11 | 17,47 | |
| 29,18 | 31,8 | 19,8 | 6,72 | 3,56 | 9,74 | 23,73 | 40,44 | 17,47 | 
|
Находим выборочное среднее арифметическое по формуле:
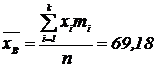
Находим исправленную дисперсию по формуле:
Стандарт отклонения
Задача 6. Найти исправленную дисперсию S 2 стандарт отклонения S для веса щитовидной железы, значения которого даны в таблице:
| xi (Г) | 60 | 68 | 70 | 72 | 90 | 100 | 105 | 120 | 125 | 130 |
| mi | 2 | 2 | 6 | 5 | 7 | 8 | 7 | 2 | 3 | 4 |
Решение
Для удобства решения задачи заполним таблицу:
Заполним таблицу:
| хi(г) | 60 | 68 | 70 | 72 | 90 | 100 | 105 | 120 | 125 | 130 |
| m i | 2 | 2 | 6 | 5 | 7 | 8 | 7 | 2 | 3 | 4 |
| хi m i (Г) | 120 | 136 | 420 | 360 | 630 | 800 | 735 | 240 | 375 | 520 |
 (Г2)
| 1156 | 676 | 576 | 484 | 16 | 36 | 121 | 676 | 961 | 1296 |
 (Г2)
| 2312 | 1352 | 3456 | 2420 | 112 | 288 | 847 | 1352 | 2883 | 5184 |
Рассчитаем суммы:
(г)
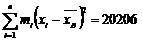(г2)
Исправленную дисперсию определяем по формуле:
,
где mi -частота появления варианты
х i -значение варианты
-сренее выборочное арифметическое
n -объем выборки.
Используя данные таблицы, находим:
(г2)
Стандарт отклонения (исправленное среднее квадратическое отклонение) находим по формуле:
(г)
Ответ: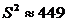 
г2, S ≈21,2 г
Задача 7. Пять измерений относительной вязкости крови человека дали следующие результаты: 4,80; 4,70; 4,85; 4,75; 4,90 (∙10-3 Па∙с).
Найти среднее арифметическое и величину доверительного интервала при доверительной вероятности 0,95.
Решение:
- Определим среднее арифметическое
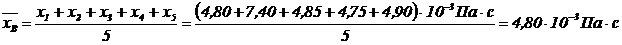
Определим стандарт отклонения среднего арифметического:
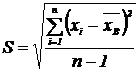
для этого составим таблицу:
| xi | 4,80 | 4,70 | 4,85 | 4,75 | 4,90 | |
| 0 | -0,1 | 0,05 | -0,05 | 0,1 | |
| 0 | 0,01 | 0,0025 | 0,0025 | 0,01 | 
|
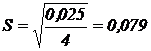
2. Определим доверительной интервал при доверительной вероятности Р=0,95.
По таблице для Р=0,95 находим коэффициент Стьюдента t =2,13.
Зная, что доверительной интервал определяется в виде интервала:
Таким образом, истинное значения относительной вязкости крови человека с вероятностью 95% лежат в интервале от 4,362∙10-3 Па∙с до 4,968∙10-3 Па∙с.
Задача 8. Двадцать одно измерение максимального кровяного давления у одного больного за период болезни дали следующие результаты (см. таблицу). Найти среднее арифметическое и величину доверительного интервала при доверительной вероятности 0,99.
| xi (мм.рт.ст.) | 98 | 160 | 136 | 128 | 130 | 114 | 123 | 134 | 128 | 128 | 107 | 123 | 125 | 129 | 132 | 154 | 115 | 126 | 132 | 136 | 130 | |
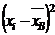
| 900 | 1024 | 64 | 0 | 4 | 196 | 25 | 36 | 0 | 0 | 441 | 25 | 9 | 1 | 16 | 676 | 169 | 4 | 16 | 64 | 4 | 
|
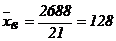
Для Р=0,99 согласно таблицы коэффициента Стьюдента t =2,53.
t · S = 2,53·13,55=34,28
тогда
93,72 < μ < 162,28
ПРАКТИЧЕСКАЯ ЧАСТЬ
