1. Метод непосредственного интегрирования

2. Метод подстановки

Примечание: При вычислении интеграла методом постановки переходим к новым пределам интегрирования для переменной t.
Метод интегрирования по частям

Вычисление площадей фигур, ограниченных линиями, уравнения которых заданы
Например: Вычислить площадь фигуры, ограниченную линиями:
 и
и  .
.
Решение: Представим искомую площадь графически.
Искомая площадьплощадь фигуры ОАСВ – заштрихована.

Находим точки пересечения линий:  , откуда x4 –x=0или х(х3 – 1)=0. Следовательно, абсциссы точек пересечений линий х1=0, х2=1, а сами точки пересечения имеют координаты (0,0) и (1,1).
, откуда x4 –x=0или х(х3 – 1)=0. Следовательно, абсциссы точек пересечений линий х1=0, х2=1, а сами точки пересечения имеют координаты (0,0) и (1,1).
В соответствии с геометрической интерпретацией определённого интеграла, определённый интеграл функции 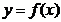 в пределах от х=х1 до х=х2, т.е.
в пределах от х=х1 до х=х2, т.е.  , численно равен площади криволинейной трапеции, ограниченной линией графика функции y = f (x), осью абсцисс и линиями x = x 1 и x = x 2. Искомая площадь SOACB равна разности площадей криволинейных трапеций:
, численно равен площади криволинейной трапеции, ограниченной линией графика функции y = f (x), осью абсцисс и линиями x = x 1 и x = x 2. Искомая площадь SOACB равна разности площадей криволинейных трапеций:
 .
.
Искомая площадь:  (кв. ед).
(кв. ед).
Ответ: Искомая площадь равна  (квадратных единиц).
(квадратных единиц).
Задачи для домашнего решения
Вычислить интегралы:
I. Метод непосредственного интегрирования
а) 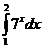 ; д)
; д)  ;
;
б)  ; е)
; е) 
в);  ж)
ж) 
г)  ; и)
; и) 
II. Метод подстановки (замены переменной)
а)  е)
е)  ;
;
б) 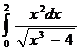 ; ж)
; ж) 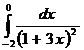 ;
;
в) 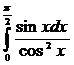 ; з)
; з)  ;
;
г)  ; и)
; и)  ;
;
III. Метод интегрирования по частям
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
Найти площадь фигуры, ограниченную линиями:
а) 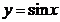 и
и  если
если 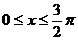 ;
;
б)  и
и  ;
;
в)  и
и  ;
;
г)  и
и  .
.
Задачи для решения на практических занятиях:
Вычислить интегралы:
а)  ; и)
; и)  ;
;
б)  ; к)
; к) 
в);  л)
л) 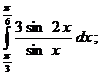
г)  ; м)
; м) 
д)  н)
н) 
е)  о)
о) 
ж)  р)
р) 
з)  с)
с) 
Найти площадь фигуры, ограниченную линиями:
а)  и
и  ;
;
б)  и
и  , если
, если 
в)  и
и 
г)  и
и 
д)  и
и 
е) 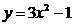 и
и 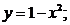
ж) 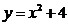 и
и 
ТЕМА №5
ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дифференциальные уравнения используются при изучении явлений и процессов в физике, химии, биологии, медицине, фармации и других областях знаний. Сформулировав задачу на языке дифференциальных уравнений, специалист любой отрасли знаний получает готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения.
Цель занятия:
1. Научиться решать дифференциальные уравнения первого порядка с разделяющимися переменными.
2. Однородные дифференциальные уравнения первого порядка.
3. Научиться решать дифференциальные уравнения второго порядка с постоянными коэффициентами.
4. Научиться решать дифференциальные уравнения второго порядка, допускающие понижение порядка.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. ОСНОВНЫЕ ПОНЯТИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у= f (x) и её производные  . Общий вид дифференциального уравнения:
. Общий вид дифференциального уравнения:
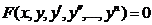 или
или

Порядок дифференциального уравнения определяется порядком наивысшей производной, входящей в данное уравнение:
 -дифференциальное уравнение первого порядка.
-дифференциальное уравнение первого порядка.
 -дифференциальное уравнение второго порядка.
-дифференциальное уравнение второго порядка.
Дифференциальное уравнение называется полным, если оно содержит в себе свободный член, производные, начиная с производной нулевого порядка, затем производных первого, второго и всех последующих порядков. Если же один из этих членов отсутствует, то уравнение называется неполным.
 -полное дифференциальное уравнение
-полное дифференциальное уравнение
 -неполное дифференциальное уравнение
-неполное дифференциальное уравнение
Дифференциальное уравнение называется приведённым, если в его правой части стоит ноль.
Дифференциальное уравнение называется обыкновенным, если искомая функция  есть функция одного аргумента.
есть функция одного аргумента.
Решением или интегралом дифференциального уравнения называется всякая функция 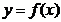 , которая будучи подставлена в дифференциальное уравнение (вместе со своими производными), превращает его в тождество.
, которая будучи подставлена в дифференциальное уравнение (вместе со своими производными), превращает его в тождество.
Всякое решение, которое содержит столько произвольных постоянных, каков порядок уравнения, называется общим решением. Решение, полученное из общего решения, путём задания произвольным постоянным определённых численных значений, называется частным решением. На практике частное решение получается из общего решения не прямым заданием значений произвольных постоянных, а исходя из тех условий, которым должно удовлетворять искомое частное решение.
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ И МЕТОД ИХ РЕШЕНИЯ
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:

Общее решение дифференциального уравнения с разделяющимися переменными даётся формулой:
 .
.
Эта формула задаёт y как функцию x неявно. Если уравнение решить относительно y, то получим явное решение дифференциального уравнения.
Пусть задано дифференциальное уравнения с разделяющимися переменными:
 ;
;
Нужно разделить переменные: в левой части уравнения собрать все у и дифференциал d у, в правой части все х и дифференциал dx.
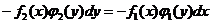 ;
;
Умножаем обе части на (-1), получаем:
 ;
;
Левую часть нужно избавить от  , а правую часть – от
, а правую часть – от  . Для этого обе части делим на
. Для этого обе части делим на  и получаем:
и получаем:
 ;
;
После сокращения получим уравнение с разделенными переменными:
 ;
;
После чего интегрируем обе части уравнения:
 .
.
Например: Найти общее и частное решения дифференциального уравнения:
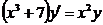 при
при  и
и  (начальные условия)
(начальные условия)
Заменяем  получаем:
получаем:
 ;
;
Левую часть освобождает от х, для чего обе части умножаем на 
 ;
;
Правую часть освобождаем от у, деля обе части на у:
 ;
;
Получили уравнение с разделенными переменными, берем интегралы левой и правой части, получаем:

Левый интеграл табличный, а правый решаем методом подстановки.
 ;
;
Раскрываем оба интеграла:
 ;
;
Для удобства постоянную интегрирования С берем под знак логарифма.
Потенцируеми получаем:
 , или
, или 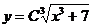 - это есть общее решение дифференциального уравнения.
- это есть общее решение дифференциального уравнения.
Находим частное решение. Для этого в общее решение подставляем начальные условия у и х и находим численное значение С:
 , откуда
, откуда 
Полученные значение С подставляем в общее решение и получаем:
 - частное решение дифференциального уравнения.
- частное решение дифференциального уравнения.
Проверка (основана на определении, что решением дифференциального уравнения называется всякая функция, приподстановки которой и её производных в уравнениеполучаем тождество):  ;
;
 ;
;
 ;
;
Возводим обе части в куб:
 ;
;
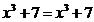 .
.
Примечание. Основные случаи потенцирования:
1. 
 ;
;
2. 

 ;
;
3. 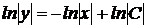
 ;
;
4. 
 .
.
3. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Уравнение  называется однородным, если функция
называется однородным, если функция  может быть представлена как функция отношения своих аргументов.
может быть представлена как функция отношения своих аргументов.
 .
.
Однородное дифференциальное уравнения первого порядка приводится к виду уравнения с разделяющимися переменными подстановкой:
 ,
,
где U – новая неизвестная функция.
Например:

Учитывая, что  получаем
получаем

Находим  :
:

Делим числитель и знаменатель правой части равенства на  , получаем:
, получаем:
 (1)
(1)
Вводим новую переменную  , (2)
, (2)
т.е.  , откуда
, откуда
 (3)
(3)
Подставляем значения из равенств (2) и (3) в равенство (1), получаем:

Путем преобразований делим переменные (уравнение решается относительно U)


Интегрируем обе части:




 (4)
(4)
Подставляем значение U из (4) во (2):

 -общее решение.
-общее решение.
4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:

если в правой части уравнения стоит ноль, то
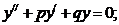
то уравнение называется однородным линейным.
Для решения такого уравнения составляется характеристическое уравнение. Характеристическим называется квадратное уравнение, полученное на основе дифференциального уравнения, в котором  заменяются новой переменной k, степень которой определяется порядком производной:
заменяются новой переменной k, степень которой определяется порядком производной:
 ;
;
Тогда  - характеристическое уравнение.
- характеристическое уравнение.
Находим корни характеристического уравнения:

1. Если корни характеристического уравнения действительные иравные 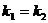 , т.е. дескременант Д=0, то решением дифференциального уравнения будет являться функция:
, т.е. дескременант Д=0, то решением дифференциального уравнения будет являться функция:
 . (1)
. (1)
2. Если корни характеристического уравнения действительные и равные числа  , Д>0, то:
, Д>0, то:
 . (2)
. (2)
3. Если корни характеристического уравнения – комплексные числа при Д<0, т.е.  , то
, то
 . (3)
. (3)
Например: Найти общее решение дифференциального уравнения:
1. 
Составляем характеристическое уравнение:
 ;
;
Находим его корни:
 ;
;
k1=k2=k=1
Подставляем полученное значение к=1 равенство (1), получаем:
 .
.
2. 

Полученные значения к1 и к2 подставляем в равенство (2), получаем:

3. 

Полученные значения α и β подставляем в равенство (3), получаем:

5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Пусть у нас есть дифференциальное уравнение, разрешенное относительно второй производной:
 ,
,
Рассмотрим виды дифференциальных уравнений второго порядка, которые допускают понижение порядка:
I. Дифференциальные уравнения не содержащие аргумента:
 (*)
(*)
Вводим новую переменную Р:

 подставляем это в (*) получаем:
подставляем это в (*) получаем:
 .
.
Получили дифференциальные уравнения первого порядка и его решением будет функция:  или
или
 Разделяем переменные, умножая обе части на
Разделяем переменные, умножая обе части на  :
:
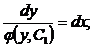

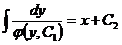 - Общее решение
- Общее решение
Пример:
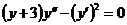 .
.
Вводим замену:  (1)
(1)
Из равенства (1) получаем:  (2)
(2)
Тогда 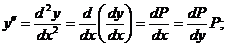 (3)
(3)
Подставляем значения  и
и  из равенств (1) и (3) в заданное уравнение и получаем:
из равенств (1) и (3) в заданное уравнение и получаем:
 .
.
Получили уравнение первого порядка.Решаем методом разделения переменными Р и у. Уравнение решается относительно Р.
 .
.
Сокращаем обе части на Р
 .
.
Делим переменные, умножая обе части на  получаем:
получаем:
 .
.
Интегрируем оба части:


Потенцируем:
 (4)
(4)
Подставляем полученное значение Р из равенства (4) в равенство (1), получаем:

Вновь получили дифференциальное уравнение первого порядка относительно переменных у и х.
Делим переменные, умножая обе части равенства на  , получаем:
, получаем:

Интегрируем:

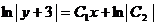 .
.
Потенцируем:

Получаем общее решение дифференциального уравнения:

II. Дифференциальные уравнения не содержащие искомой функции:
 (**)
(**)


Тогда уравнение (**) примет вид:
 .
.
Решением этого уравнения будет функция: 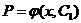


 - Общее решение
- Общее решение
Пример:

Вводим замену: 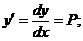 (1)
(1)
Тогда  (2)
(2)
Подставляем значения  и
и  из равенств (1) и (2) в исходное уравнение и получаем:
из равенств (1) и (2) в исходное уравнение и получаем:
 .
.
Делим переменные, умножая обе части на  получаем:
получаем:
 .
.
Интегрируем оба части равенства:


Потенцируем:
 (3)
(3)
Подставляем значение Р из равенства (3) в равенство (1) и получаем:
 .
.
Делим переменные, умножая обе части равенства на  , и интегрируем:
, и интегрируем:

 - Общее решение
- Общее решение
III. Дифференциальные уравнения не содержащее искомой функции и её производной:
 (***)
(***)
Подстановка: 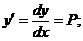
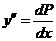 подставляем в (***)
подставляем в (***)



 - Общее решение
- Общее решение
Например: Найти общее решение дифференциального уравнения:

Вводим подстановку:  (1)
(1)
Тогда  (2)
(2)
Подставляем значения  из равенства (2) в исходное уравнение:
из равенства (2) в исходное уравнение:
 .
.
Делим переменные, умножая обе части равенства на  получаем:
получаем:
 .
.
Решаем полученное уравнение, интегрируя обе части:

и получаем;
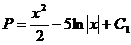 (3)
(3)
Подставляем значение Р из равенства (3) в равенство (1), получаем:
 .
.
Делим переменные, умножая обе части равенства на  , и интегрируем:
, и интегрируем:


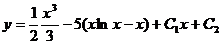 .
.
Таким образом,
 - Общее решение
- Общее решение
Примечание. Решаем интеграл  методом интегрирования по частям:
методом интегрирования по частям:

ПРАКТИЧЕСКАЯ ЧАСТЬ






