Явление, которое при неоднократном наблюдении или воспроизведении одного и того же опыта протекает каждый раз несколько по иному, называется случайным. Случайность объективно существует в окружающем нас мире вследствие принципиальной невозможности проследить все причинные связи изучаемого явления с бесчисленным множеством других явлений. Отдельное явление представляет собой следствие какого-то другого и само служит причиной последующего, но проследить связь между условиями и конечным результатом часто затруднительно или даже невозможно. Однако случайные явления, если их число достаточно велико, подчиняются определенным закономерностям, изучаемым в теории вероятностей.
Теория вероятностей –это раздел математики, в котором изучаются закономерности, присущие случайным событиям, величинам и процессам массового характера.
Теория вероятностей нашла применение в теории эпидемий, в разработке медицинских методов математической диагностики, в организации здравоохранения и т.д.
Цель занятия: Научиться применять при решении задач основные понятия и теоремы теории вероятностей.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Массовые явления и процессы характеризуются многократным повторением при постоянных условиях некоторых наблюдений, опытов, операций. Осуществление некоторого комплекса условий, который может быть воспроизведен сколько угодно большое число раз, называется испытанием. Результат, исход испытания называют событием. Случайным событием в теории вероятностей называют всякое событие, которое в результате испытания может произойти или не произойти. Случайные события обозначают большими буквами латинского алфавита: A, B, C …
1. Основные виды случайных событий
Если в результате испытания непременно должно появиться хотя бы одно из рассматриваемых событий, то их называют полной группой событий.
Примеры событий, образующих полную группу:
1. Выпадение герба и выпадение цифры при бросании монеты.
2. Появление 1,2,3,4,5,6 очков при бросании игральной кости - симметричного кубика, на гранях которого нанесенно различное число очков от 1 до 6.
3. При измерении давления крови человека оно может оказаться нормальным, пониженным, повышенным.
Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании. Например, при бросании игральной кости: событие А - появление трех очков, событие В – появление нечетного числа очков. В этом случае события А и В – совместные.
Несколько событий называют несовместными, если в результате испытания осуществление одного из них исключает осуществление остальных. Например, давление крови человека при одном измерении не может быть одновременно нормальным и повышенным или нормальным и пониженным.
Два несовместных события, составляющих полную группу, называются противоположными:А и 
. Напрмер, наличие и отсутствие заболевания; выпадение герба и выпадение цифры при бросании монеты.
Понятие совместности или несовместности событий связано с тем, какое испытание имеется в виду. Одни и теже события А и В могут оказаться несовместными в одном испытании и совместными в другом. Например, попадание и промах являются несовместными событиями, если испытание состоит в том, что производится один выстрел. Однако, попадание и промах совместны, если испытание состоит в том, что призводится несколько выстрелов.
2. Понятие вероятности события
Предположим, что производится массовое обследование населения. Например, определяется температура тела, измеряется давление крови, производится анализ мочи, крови. При этом происходят события:
А – наличие повышенной температуры;
В – наличие нормального давление крови;
С – наличие повышенного давления;
D – наличиесахара в моче;
Е – пониженное содержание лейкоцитов в крови и т.д.
Каждое из перечисленных событий обладает какой-то степенью возможности: одно – большей, другое – меньшей. Чтобы количественно сравнивать события по степени их возможности, с каждым событием связывают определенное число, которое тем больше, чем более возможно событие. Такое число называют вероятностью события. В качестве единицы измерения вероятности принимают вероятность достоверного события – такого события, которое в результате испытания непременно должно произойти. Например, достоверное событие – обнаружение лейкоцитов при проведении анализа крови. Противоположным по отношению к достовеному событию является невозможное событие – такое событие, которое в данном испытании не может произойти. Например, отсутствие лейкоцитов в крови человека – невозможное событие. Если приписать достоверному событию вероятность, равную единице, а невозможному событию, равную нулю, то все другие события – возможные, но не достоверные,будут характеризоваться вероятностями, составляющими какую-то долю единицы:
0 ≤ Р ≤ 1
3. Классическое определение вероятности
Исторически закономерности случайных явлений изучались на материале азартных игр. Азартные игры создавались таким образом, чтобы их исходы были независимы от поддающихся наблюдению условий, то есть были чисто случайными. Схемы азартных игр дают исключительно простые модели для изучения специфических законов случайных явлений, для которых вероятности возможных исходов испытаний можно оценить непосредственно из условий испытаний. Для этого испытания должны обладать симметрией возможных исходов.
Рассмотрим, например, испытание, состоящее в бросании игрального кубика. В силу симметрии кубика есть основания считать, что все шесть возможных исходов испытания одинаково возможны. Это позволяет предполагать, что при многократном бросании кубика все шесть граней будут выпадать примерно одинаково часто. Для правильно выполненного кубика это предположение действительно оправдывается:при многократном бросании кубика каждая его грань выпадает примерно в одной шестой доле случаев бросания. Отклонение этой доли от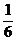 
тем меньше, чем больше число испытаний произведено. Для всякого испытания, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.
События, образующие полную группу попарно несовместных и равновозможных событий, называют элементарными. Элементарными событиями, например, являются: появление герба и цифры при бросании монеты; появление 1,2,3,4,5,6 очков при бросании игрального кубика.
Элементарные события такой группы называют благоприятствующими осуществлению события А, если осуществление любого из элементарных событий влечет за собой осуществление события А. Например, появление 2,4,6 очков при бросании игрального кубика благоприятствует осуществлению события А, заключающегося в появлении четного числа очков.
Классической вероятностью Р(А) события А называется отношение числа m элементарных событий, благоприятствующих событию А, к числу n всех элементарных событий, то есть
.
Задача:
В коробке находится 4 красных и 6 синих карандашей. Наугад извлекаем 1 карандаш. Определить вероятность, что он будет красным.
Решение:
Число элементарных событий, благоприятствующих извлечению красного карандаша событие А, m =4. Общее число элементарных событий n =10.
Вероятность извлечения красного карандаша 
.
4. Статистическое определение вероятности
Если в одних и тех же условиях произведена серия из n испытаний, в каждом из которых могло появиться или не появиться некоторое событие А, то отношение числа испытаний, в которых появилось событие А, к общему числу произведенных испытаний, называется относительной частотой события А, или частотой.
Частота события вычисляется на основании результатов испытаний по формуле:
,
где m – число появлений события А,
n – число испытаний.
Увеличение числа испытаний уменьшает колебание частоты события около некоторой постоянной величины.
Статистической вероятностью случайного события называют предел, к которому стремится частота события при неограниченном увеличении числа испытаний:
.
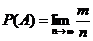Практически за вероятность случайного события можно принять относительную частоту события при большом числе испытаний.
Задача:
При обследовании 250 человек путем флюорографии были выявлены следующие заболевания: у 7 человек–опухоль в легких, у 3 человек–плеврит, у 5 человек–остаточные явления после пневмонии. Найти вероятность этих заболеваний, выявленных с помощью флюорографии.
Дано: Решение:
n =250 
;
m1=7 
;
m2=3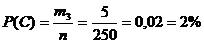 
.
m3=5
P(A)-?
P(В)-?
P(C)-?
5. Понятие условной вероятности
Рассмотрим сложное событие, являющееся результатом двух последовательных испытаний. В первом испытании осуществилось событие А, а во втором - событие В. Проведение первого испытания может влиять на вероятность осуществления второго, а может и не влиять. В первом случае события А и В называются независимыми, а во втором – зависимыми. В качестве примера рассмотрим модель урны с белыми и черными шарами. Тогда событие А –из урны извлечен белый шар, событие В – из урны извлечен черный шар. После того, как был извлечен белый шар, можно вернуть шар в урну, а можно и не возвращать. В первом случае перед вторым испытанием мы возвращаем систему в исходное состояние, и, следовательно, второе испытание (извлечение второго шара) будет независимо от первого. Во втором случае, когда мы не возвращаем шар, ситуация изменится: количество шаров в урне изменится, и изменится соотношение белых и черных шаров в урне, а следовательно, в этом случае изменятся вероятности, характеризующие события А и В.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В).
Задача:
К экзамену студент выучил только 20 билетов из 30. Какова вероятность, что ему достанется невыученный билет (событие А)? Изменится ли вероятность этого события, если раньше другой студент уже вытащил один билет из тех, что не выучен первым студентом (событие В)?
Дано: Решение
n=30 
,
m1=10 
.
P(B/A)-?
2. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. Теорема сложения вероятностей
Пусть дана полная группа событий А,В,С, D, которым соответствуют частоты (вероятности)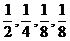 
. Какова вероятность, что в результате испытания произойдет событие А или В? В этом вопросе подразумевается, что благоприятный исход испытания состоит в осуществлении события А или в осуществлении события В. Символически это можно записать Р(А или В). Очевидно, что искомая вероятность должна быть больше вероятности осуществления события А и большее вероятности осуществления события В.
Допустим, что было проведено n испытаний, в которых в m1 случаях осуществилось событие А, а в m 2 случаях событие В. Всего благоприятных для осуществления события А или события В случаев было m 1 + m 2 , а частота (вероятность) осуществления события А или события В соответственно равна 
, то есть
Р (А или В) = 
;
Полученное выражение иллюстрирует теорему сложения вероятностей: Вероятность наступления в некотором испытании какого–либо одного события (безразлично какого именно) А1, А2,..., А n равна сумме вероятностей этих событий, если события несовместны:
Р(А1 или А2 или … А n)=Р(А1)+ P (A 2)+…+Р(А n);
Следствие 1: Сумма вероятностей противоположных событий равна 1:
Р(А)+Р()=1.
Задача:
Вероятность наступления хотя бы одного вызова врача в течение часа Р(А)=0,85. Найти вероятность того, что в течение часа не последует вызова (событие В).
Дано: Решение:
P (A)=0,85 Событие В является противоположным событию А.
Р(В)=? Сумма их вероятностей
Р(А) + Р(В) =1,
откуда Р(В)=1–Р(А)=1–0,85=0,15.
Следствие 2: Сумма вероятностей событий, образующих полную группу, равна 1:
Р(А1)+Р(А2)+…+Р(А n)=1, или
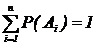- Данное выражение называют условием нормировки.
Задача:
Медсестра обслуживает три палаты. Вероятность поступления вызова из первой палаты–0,2, из второй–0,4. Какова вероятность того, что ближайший вызов будет из третьей палаты?
Дано: Решение:
Р(А)=0,2 Согласно условию нормировки, Р(А)+Р(В)+Р(С)=1,
Р(В)=0,4 тогда Р(С)=1–Р(А)–Р(В)
P (C)-? Р(С)=1–0,2–0,4=0,4.
2. Теорема умножения вероятностей
Предположим, что проводится испытание, заключающееся в бросании правильно выполненного игрального кубика два раза подряд. Возможные результаты такого испытания представим в виде таблицы:
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 |
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 |
| 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 |
| 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 |
| 6,1 | 6,2 | 6,3 | 6,4 | 6,5 | 6,6 |
В каждой ячейке таблицы первая цифра – результат первого бросания, вторая цифра – результат второго бросания.
Как видно из таблицы, возможны 36 вариантов исхода двукратного бросания кубика. Попробуем рассчитать вероятность выпадения два раза подряд числа 6. Для правильно выполненного кубика все приведенные в таблице исходы равновероятны и, следовательно, выпадение двух шестерок, как и выпадение любой другой пары одинаковых чисел, имеет вероятность, равную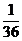 
. Но 
, то есть вероятность выпадения подряд двух шестерок равна произведению вероятности выпадения числа 6 на самое себя. Данный пример иллюстрирует теорему умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей.
Для случая двух независимых событий А и В:
Р(Аи В)=Р(А)·Р(В).
Так как события А и В независимы, то каждому из m 1 случаев, благоприятствующих событию А, соответствуют m 2 случаев, благоприятствующих событию В. Таким образом, общее число случаев, благоприятствующих появлению событий А и В, равно, m 1 · m 2 а общее число равновозможных событий равно n 1 · n 2, где n 1 и n 2 – числа равновозможных событий соответственно для А и В. Отсюда вероятность совместного появления событий равна: 
.
Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых событий.
Вероятность наступления в некотором испытании одновременно двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое события имело место:
Р(А и В)=Р(А)·Р(B / A)=Р(В)·Р(A / B) – формула Байеса
При решении задач необходимо:
1. Выяснить, являются ли эти события независимыми или зависимыми;
2. Определить вероятности каждого отдельного события;
3. Определить вероятность одновременного наступления этих событий.
Задача:
В урне находится 10 белых и 20 черных шаров. Определить вероятность вынимания двух белых шаров подряд.
Дано: Решение:
m 1 =10 Вероятность вынимания первого белого шара равна
m 2 =20 
n = m 1 + m 1 =30 Вероятность вынимания второго белого шара равна:
P (A и В)-? 
Тогда вероятность вынимания двух белых шаров подряд будет:
Р(А и В)=Р(А)·Р(B / A)=0,33·0,31≈0,1
Задача:
Считая, что рождение девочки или мальчика – это независимые и равновозможные события, определить вероятность появления в семье подряд трех девочек.
Дано: Решение:
P (D)=0,5 Согласно теореме умножения вероятностей для
P (D 1 и D 2 и D 3)-? независимых событий:
Р(D 1 и D 2 и D 3)=[Р(D)]3=0,53=0,125 (12,5%)
