Средняя величина, вычисленная на основании ряда чисел, каждое из которых встречается один раз, называется простой средней арифметической:
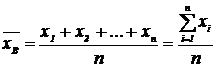
Если значение признака х1 появилось m 1 раз
х2 появилось m 2 раз
…………………………………
xk появилось mk раз
причем m 1 + m 2 +…+ mk = n, то вычисляется взвешенная средняя арифметическая:
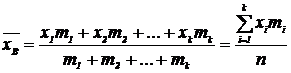
Если при обработке экспериментальных данных составляется интервальный вариационный ряд, то n наблюдавшихся значений величины (х1,х2… xn) группируются в N интервалов с одинаковой длиной интервала Δх. Среднее значение интервала обозначили 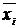 , где i =1,2,3,..., N. Число значений, попавших в интервал обозначается через mi, тогда:
, где i =1,2,3,..., N. Число значений, попавших в интервал обозначается через mi, тогда:
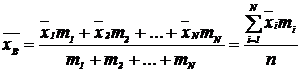
При увеличении объема выборки (n) выборочная средняя стремится к генеральной средней, а это означает, что выборочная средняя есть состоятельная оценка генеральной средней.
2. Модой (Мо) называется наиболее вероятное значение случайной величины или значение величины с наибольшей частотой появления.
3. Медианой(Ме) называется значение варианты, стоящей в центре вариационного ряда, т.е. эта варианта делит вариационный ряд на две равные по числу значений части при условии, что объем выборки есть нечетное число. Если объем выборки четной число то медиана определяется полусуммой двух вариант, стоящих в центре вариационного ряда.
Например:
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | n =7 |
Ме =4,9
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | 6,9 | n =8 |

- ВЫБОРОЧНАЯ ДИСПЕРСИЯ И ВЫБОРОЧНОЕ СРЕДНЕЕ
КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Выборочной дисперсией ДВ называют среднее арифметическое квадратов отклонения вариант от их среднего значения.
Если все варианты выборки объема n имеют различные значения х1,х2,.., xn, то
 (1)
(1)
Если значение варианты (признака)
х1 появляется m 1 раз
х2 появляется m 2 раз
…………………………………
xk появляется mk раз,
причем 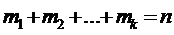 , то
, то
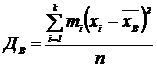 (2)
(2)
Выборочным средним квадратическим отклонением или стандартом отклонения называется квадратный корень из выборочной дисперсии:
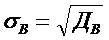
Дисперсию генеральной совокупности нельзя оценить по значениям выборочной дисперсии (это положение можно доказать) поэтому вводится понятие «исправленная дисперсия», которая определяется по формуле:
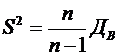
Для формулы (1): 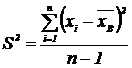
Для формулы (2): 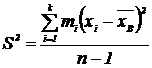
Тогда исправленное среднее квадратическое отклонение 
- ДОВЕРИТЕЛЬНЫЕ ВЕРОЯТНОСТИ И УРОВНИ ЗНАЧИМОСТИ.
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ И ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ
Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. Поэтому при небольшом объеме выборки пользуются интервальными оценками.
В этом случае указывается интервал (доверительный интервал или доверительные границы), в котором с определенной (доверительной) вероятностью Р находится истинное значение исследуемой величины (например, среднее значение генеральной совокупности).
Доверительная вероятность Р определяет вероятность, с которой осуществляется неравенство:
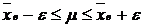 (*)
(*)
где ε – положительное число, характеризующее точность оценки.
Кроме доверительной вероятности используют «противоположенное» понятие – уровень значимости β:
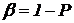
Он выражает вероятность непопадания истинного значения исследуемой величины в доверительный интервал.
Наиболее часто в медицине доверительная вероятность Р принимается равной: 0,95; 0,99 и 0,999.
Если генеральная совокупность распределена по нормальному закону, тогда в неравенстве (*):

Для нахождения τ используются специальные таблицы Ф- функции.
Тогда доверительный интервал для оценки математического ожидания нормального распределения определится неравенством:

- ИНТЕРВАЛЬНАЯ ОЦЕНКА ПРИ МАЛОЙ ВЫБОРКЕ
При достаточно большом объеме выборки можно сделать вполне надёжные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема (n <30). Кроме того, почти всегда оказывается неизвестной генеральная дисперсия.
Имея выборку, можно найти лишь исправленную выборочную дисперсию S 2 и выборочную среднюю 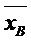 . Выразим отклонение выборочного среднего от генерального через S и некоторый параметр t.
. Выразим отклонение выборочного среднего от генерального через S и некоторый параметр t.
 или
или 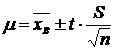
Или представим это в виде интервала:

где t- коэффициент Стьюдента, который находится по таблицам, согласно заданному объему выборки и доверительной вероятности(приложение 4).






