1. Производная от неопределённого интеграла равна подинтегральной функции:
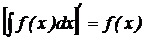 .
.
2. Дифференциал от неопределённого интеграла равен подинтегральному выражению:
 .
.
3. Интеграл от дифференциала первообразной функции равен самой первообразной, сложенной с произвольной постоянной:
 .
.
4. Постоянный множитель можно вынести за знак интеграла:
 ; где а- const
; где а- const
5. Интеграл алгебраической суммы функций равен алгебраической сумме интегралов этих функций:
.
3. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 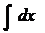 = х+С; 10.
= х+С; 10. 
2.  11.
11. 
3.  12.
12. 
4.  13.
13. 
5. 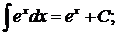 14.
14. 
6. 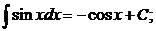 15.
15. 
7.  16.
16. 
8.  17.
17. 
9. 
ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
1. Метод непосредственного интегрирования
Метод непосредственного интегрирования основан на преобразовании подинтегральной функции, применении свойств неопределённого интеграла и приведении подинтегрального выражения к табличной форме.
Например:
1) 

Проверка (на основании свойства №2 неопределённого интеграла):

2) 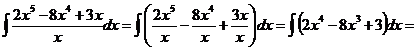

Проверка (на основании свойства №1 неопределённого интеграла): 

2. Метод подстановки (замены переменной)
Этот метод основан на введении новой переменной. В интеграле  сделаем подстановку:
сделаем подстановку:
 , тогда
, тогда
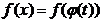 ;
;
 ;
;
Следовательно, получим:

Например:
1) 
Проверка: 
2) 
Проверка (на основании свойства №2 неопределённого интеграла):

3. Интегрироване по частям
Пусть u и v - дифференцируемые функции. Раскроем дифференциал произведения этих функций:
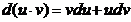 ,
,
откуда 
Проинтегрируем полученное выражение:

Тогда

или

Например:
Проверка (на основании свойства №1 неопределённого интеграла):


2) 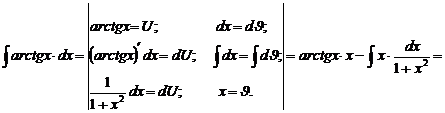

Решаем 
Проверка (на основании свойства №1 неопределённого интеграла):


ПРАКТИЧЕСКАЯ ЧАСТЬ
Задачи для домашнего решения
Найти интеграл:
I. Метод непосредственного интегрирования
а)  ; е)
; е)  ;
;
б) 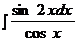 ; ж)
; ж) 
в) 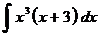 ; з)
; з) 
г)  ; и)
; и) 
д)  ; к)
; к) 
II. Метод подстановки (замены переменной)
а)  ; е)
; е)  ;
;
б)  ; ж)
; ж) 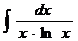 ;
;
в)  ; з)
; з)  ;
;
г) 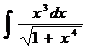 ; и)
; и)  ;
;
д)  ; к)
; к)  .
.
III. Метод интегрирования по частям
а) 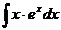 ; в)
; в)  ; д)
; д) 
б)  ; г)
; г)  ; е)
; е) 
Задачи для решения на практических занятиях:
I. Метод непосредственного интегрирования
а)  ; ж)
; ж)  ;
;
б)  ; з)
; з)  ;
;
в) 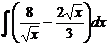 ; и)
; и) 
г)  ; к)
; к) 
д)  ; л)
; л) 
е)  ; м)
; м) 
II. Метод подстановки (замены переменной)
а) 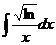 ; ж)
; ж) 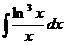 ;
;
б) 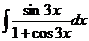 ; з)
; з) 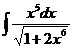 ;
;
в)  ; и)
; и)  ;
;
г)  ; к)
; к)  ;
;
д)  ; л)
; л)  ;
;
е)  ; м)
; м) 
III. Метод интегрирования по частям
а)  ; д)
; д)  ;
;
б)  ; е)
; е)  ;
;
в)  ; ж)
; ж) 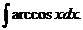
г)  ;
;
ТЕМА №4
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
При математических расчётах часто требуется найти приращение первообразной функции при изменении её аргумента в заданных пределах. Такую задачу приходится решать при вычислении площадей и объёмов различных фигур, при определении среднего значения функции, при вычислении работы переменной силы. Эти задачи могут быть решены вычислением соответствующих определённых интегралов.
Цель занятия:
1. Научиться вычислять определённый интеграл с помощью формулы Ньютона-Лейбница.
2. Уметь применять понятие определённого интеграла для решения прикладных задач.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Рассмотрим задачу о нахождении площади криволинейной трапеции.
Пусть дана некоторая функция y = f (x), график которой изображён на рисунке.

Рис 1. Геометрический смысл определенного интеграла.
На оси 0х выберем точки “ a ” и “в” и восстановим из них перпендикуляры до пересечения с кривой. Фигура ограниченная кривой, перпендикулярами и осью 0х называется криволинейной трапецией. Разобьём интервал  на ряд небольших отрезков. Выберем произвольный отрезок
на ряд небольших отрезков. Выберем произвольный отрезок  . Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:
. Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:
 .
.
Тогда площадь всех достроенных прямоугольников в интервале  будет равна:
будет равна:
 ;
;
Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:
 ;
;
Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.
Интегральная сумма есть сумма произведений приращения аргумента на значение функции f (x), взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.
Функция f (x ) в некотором интервале от х=а до х=в интегрируема, если существует такое число, к которому стремится интегральная сумма при D х ® 0. В этом случае число J называют определённым интегралом функции f (x) в интервале  :
:

 ;
;
где ] а, в [ – область интегрирования,
а –нижний предел интегрирования,
в –верхний предел интегрирования.
Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале ] а, в [ и осью абцисс.
2. СВЯЗЬ МЕЖДУ ОПРЕДЕЛЁННЫМ И НЕОПРЕДЕЛЁННЫМ ИНТЕГРАЛАМИ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
Неопределённый интеграл - это совокупность первообразных функций. Определённый интеграл - это число. Связь между ними задаётся формулой Ньютона-Лейбница.
Теорема. Значение определённого интеграла равно разности значений любой первообразной от подинтегральной функции, взятой при верхнем и нижнем пределами интегрирования:

Например:  .
.
3. СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Определённый интеграл не зависит от обозначения переменной интегрирования:
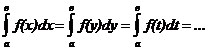 ;
;
2. Определённый интеграл от алгебраической суммы конечного числа непрерывных функций  , заданных на отрезке
, заданных на отрезке  равен алгебраической сумме определённых интегралов от слагаемых функций:
равен алгебраической сумме определённых интегралов от слагаемых функций:
 ;
;
3. Постоянный множитель можно вынести за знак интеграла:
 ;
; 
4. Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит свой знак на противоположный:
 ;
;
5. Если а=в, то  ;
;
6. Если отрезок интегрирования  разбить на две части
разбить на две части  и
и  , то:
, то:
 ;
;
7. Если подинтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, т.е. если  , то
, то
 ;
;
8. Значение определённого интеграла заключено между произведениями наибольшего и наименьшего значений подинтегральной функции на длину интервала интегрирования:
 , где M, m – наибольшее и наименьшее значения функции
, где M, m – наибольшее и наименьшее значения функции  на отрезке
на отрезке  : m £
: m £  £ M.
£ M.
9. Определённый интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=С отрезка интегрирования  на длину отрезка (в-а):
на длину отрезка (в-а):
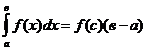 ,
,
где f (c) - среднее значение функции в интервале.







