Теорема: Если функция 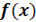 , дифференцируемая на интервале ]a, b[, имеет в точке
, дифференцируемая на интервале ]a, b[, имеет в точке 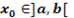 экстремум, то ее производная в этой точке равна нулю:
экстремум, то ее производная в этой точке равна нулю:
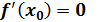 (необходимое условие)
(необходимое условие)
Теорема: Если производная  функции
функции  при некотором значении аргумента
при некотором значении аргумента 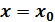 равна нулю и при переходе аргумента через это значение меняет знак с плюса на минус, то при
равна нулю и при переходе аргумента через это значение меняет знак с плюса на минус, то при 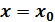 функция имеет максимум; если при переходе аргумента через это значение производная меняет знак с минуса на плюс, то при
функция имеет максимум; если при переходе аргумента через это значение производная меняет знак с минуса на плюс, то при
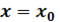 функция имеет минимум. Если при переходе через точку
функция имеет минимум. Если при переходе через точку 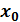 производная функции не меняет знака, то в этой точке функция
производная функции не меняет знака, то в этой точке функция  экстремума не имеет (достаточное условие).
экстремума не имеет (достаточное условие).
Правило исследования дифференцируемой функции на
Экстремумы с помощью первой производной
Рассмотрим данное правило на примере: 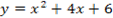
1. Находят производную функции:  .
.
2.Находят критическое значение аргумента, для чего 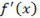 приравнивают к нулю и получают действительные корни уравнения (если корни уравнения мнимые, то экстремума нет).
приравнивают к нулю и получают действительные корни уравнения (если корни уравнения мнимые, то экстремума нет).
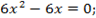
| |
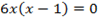
| |

|
Критические точки







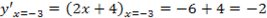
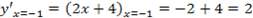
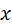 =-2 – это точка минимума.
=-2 – это точка минимума.
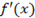 , при переходе через критическую точку х=х0
, при переходе через критическую точку х=х0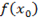
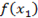 min
min
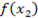 max
max
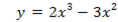
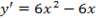


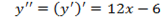 ;
;

 выпукла в интервале
выпукла в интервале 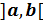 , если при всех значениях аргумента
, если при всех значениях аргумента  этого интервала вторая производная отрицательна.
этого интервала вторая производная отрицательна.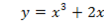 .
.
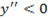
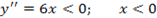
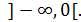
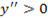

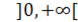 .
. 
