1. Найти производную функций:
а) 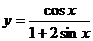 ; в)
; в) 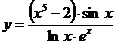 ;
;
б)  ; г)
; г) 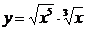 .
.
2. Найти производные следующих сложных функций:
а)  ; г)
; г) 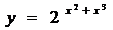 ;
;
б)  ; д)
; д) 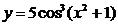 ;
;
в) 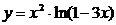 ; е)
; е) 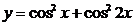 .
.
3. Найти производную второго порядка функций:
а) 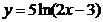 ; в)
; в) 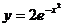 .
.
б) 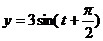 ;
;
4. Найдите скорость и ускорение точки, совершающей гармонические колебания по закону:  где S 0,ω,φ- const.
где S 0,ω,φ- const.
5. При ламинарном течении крови по крупным сосудам её слои имеют различную скорость в зависимости от расстояния x от оси сосуда:  , где DP-разность давления на участке сосуда длиной
, где DP-разность давления на участке сосуда длиной 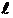 ; R-радиус сосуда; h - коэффициент вязкости крови. Найдите величину градиента скорости на расстоянии x от оси сосуда.
; R-радиус сосуда; h - коэффициент вязкости крови. Найдите величину градиента скорости на расстоянии x от оси сосуда.
6. Найти дифференциал следующих функций:
а) 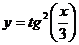 ; г)
; г) 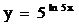 ;
;
б)  в)
в)  .
.
7. Найти полный дифференциал следующих функций:
а) 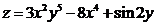 ; б)
; б)  .
.
8. Приближенно вычислить:
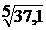 ;
;  ;
; 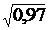 ;
;
31,8; 122,1;
ln15,1; ln8,4; ln0,79;
lg18,4; lg1032;
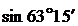 ;
;  ;
; 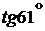 ;
; 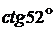 .
.
Задачи для решения на практическом занятии
1. Найти производные следующих функций:
а) 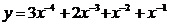 ; в)
; в) 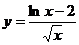 .
.
б)  ;
;
2. Найти производные следующих сложных функций:
а) 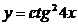 ; г)
; г)  ;
;
б)  ; д)
; д) 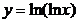 ;
;
в) 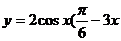 ); е)
); е) 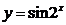 .
.
3. а) Найти производные второго порядка следующих функций:
а) 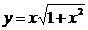 ; в)
; в) 
б) 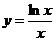 ; г)
; г) 
б) Уравнение движения точки имеет вид: 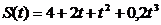 .
.
Определите мгновенную скорость и ускорение точки.
4. а) Зависимость между количеством x вещества, полученного в некоторой химической реакции, и временем t выражается уравнением: 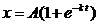 , где A, k - постоянные.
, где A, k - постоянные.
Определить скорость реакции.
б) Растворение лекарственных веществ из таблеток подчиняется уравнению: C=C0 e-kt, где C - количество лекарственного вещества в таблетке, оставшееся ко времени растворения t;
C0 - исходное количество лекарственного вещества в таблетке;
k -постоянная скорости растворения.
Определить скорость растворения лекарственных веществ из таблеток.
в) Рост числа бактерий подчиняется закону 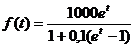 . Определить скорость роста числа бактерий.
. Определить скорость роста числа бактерий.
г) Смещение в ответ на одиночное мышечное сокращение (единичный импульс) описывается уравнением: 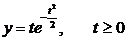 .
.
Определить скорость и ускорение в зависимости от времени.
5. Найти дифференциалы следующих функций:
а)  ;
;
б)  ;
;
6. Найти полный дифференциал следующих функций:
а) 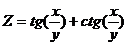 ;
;
б)  ;
;
в) 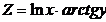 .
.
7. Вычислить приближенно:
а) 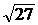 ;
; 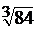 ;
; 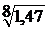 ;
;
б) 28,3; 51,9; 33,2;
в) ln1,18; ln 7,5; ln 38;
г) lg115; lg 1181.
ТЕМА №2
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Умение применять производные к исследованию функций позволяет исследовать весь ход изменения функции и строить её график. При математических расчетах часто требуется определить максимальное значение функции, что часто используется при решении медико-биологических задач.
Цель занятия
- Научиться исследовать функции и строить их графики.
- Использовать теорию экстремумов для решения прикладных задач.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ НА ИНТЕРВАЛЕ
Функция  называется возрастающей [убывающей] на некотором интервале ]a, b[, если для любых точек x1 и x2, принадлежащих данному интервалу из неравенства
называется возрастающей [убывающей] на некотором интервале ]a, b[, если для любых точек x1 и x2, принадлежащих данному интервалу из неравенства 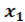 <
< 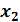 , следует неравенство
, следует неравенство 
 [
[  ]. Представим графики этих функций.
]. Представим графики этих функций.

| 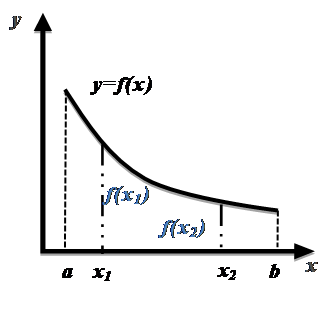
|

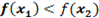
| 
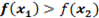
|
| Рис1. Возрастающая функция | Рис2. Убывающая функция |






