Обозначим через (Х,,А) игру двух лиц с нулевой суммой, в которой игрок 1 выбирает стратегию х Î Х, игрок 2 Î U, после чего игрок 1 получает выигрыш А = А (х, ) за счёт игрока 2.
Определение. Стратегия х1 игрока 1 доминирует (строго доминирует) над стратегией х2, если
А (х1, ) ³ А (х2, )(А (х1, ) А (х2, )), Î U.
Стратегия 1 игрока 2 доминирует (строго доминирует) над стратегией 2, если
А (х, 1) £ А (х, 2)(А (х, 1) А (х, 2)), х Î Х.
При этом стратегии х2 и 2 называются доминируемыми (строго доминируемыми).
Спектром смешанной стратегии игрока в конечной антагонистической игре называется множество всех его чистых стратегий, вероятность которых согласно этой стратегии положительна.
Свойство 1. Если чистая стратегия одного из игроков содержится в спектре некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной чистой стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.
Свойство 2. Ни одна строго доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.
Игра ¢ = (Х¢,¢,А¢) называется подыгрой игры (Х,,А), если Х¢Ì Х, U¢Ì U, а матрица А¢ является подматрицей матрицы А. Матрица А¢ при этом строится следующим образом. В матрице А остаются строки и столбцы, соответствующие стратегиям Х¢ и U¢, а остальные “вычеркиваются”. Всё то что “останется” после этого в матрице А и будет матрицей А¢.
Свойство 3. Пусть = (Х,,А) конечная антагонистическая игра, ¢ = (Х х¢,,А) подыгра игры , а х¢ чистая стратегия игрока 1 в игре , доминируемая некоторой стратегией 
, спектр которой не содержит х¢. Тогда всякое решение (хо, о, u) игры ¢ является решением игры .
Свойство 4. Пусть = (Х,,А) конечная антагонистическая игра, ¢ = (Х, ¢,А) подыгра игры , а ¢ чистая стратегия игрока 2 в игре , доминируемая некоторой стратегией 
, спектр которой не содержит ¢. Тогда всякое решение игры ¢ является решением .
Свойство 5. Если для чистой стратегии х¢ игрока 1 выполнены условия свойства 3, а для чистой стратегии ¢ игрока 2 выполнены условия свойства 4, то всякое решение игры ¢ = (Х х¢, ¢,А) является решением игры = (Х,,А).
Свойство 6. Тройка (хо, о, u) является решением игры = (Х,,А) тогда и только тогда, когда (хо, о, кu +а) является решением игры (Х,,кА+а), где а любое вещественное число, к 0.
Свойство 7. Для того, чтобы хо = (
) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры u, необходимо и достаточно выполнение следующих неравенств
(j = 
) 
Аналогично для игрока 2: чтобы о = (
,..., 
,..., 
) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:
(i = 
) 
Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, ) и u решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следующими уравнениями
, 
получим решение матричной игры.
Таким образом, решение матричной игры сводится к нахождению неотрицательных параметров решений линейных неравенств (*) (**) и линейных уравнений (***). Однако это требует большого объёма вычислений, которое растёт с увеличением числа чистых стратегий игроков. (Например для матрицы 3 
3 имеем систему из 6 неравенств и 2 уравнений). Поэтому в первую очередь следует, по возможности используя свойства 2 и 3, уменьшить число чистых стратегий игроков. Затем следует во всех случаях проверить выполнение неравенства
= .
Если оно выполняется, то игроки имеют чистые оптимальные стратегии (игрок 1 чистую максиминная, а игрок 2 чистую минимаксная). В противном случае хотя бы у одного игрока оптимальные стратегии будут смешанные. Для матричных игр небольшого размера эти решения можно найти, применяя свойства 1 5.
Замечание. Отметим, что исключение доминируемых (не строго) стратегий может привести к потере некоторых решений. Если же исключаются только строго доминируемые стратегии, то множество решений игры не изменится.
Пример 3. Пусть = (Х,,А), где Х = 1, 2, 3, 4; = 1, 2, 3, 4, а функция выигрыша А задана следующим образом:
где С 0.
Решение. Прежде всего заметим, что по свойству 6 достаточно решить игру 1 = (Х,,А), где А1 = 
А. В матричной форме игра 1 определяется матрицей выигрышей
Элементы четвёртой строки этой матрицы “ £ соответствующих элементов третьей строки и поэтому третья стратегия игрока 1 доминирует над четвёртой. Кроме того, элементы первого столбца матрицы А1 “ ³ соответствующих элементов второго столбца, Следовательно, вторая стратегия игрока 2 доминирует над его первой стратегией.
Далее, из свойства 5 следует, что всякое решение игры 2 = (Х 4, 1, А1) является решением игры 1. В матричной форме игру 2 можно представить матрицей
.
Очевидно, что элементы второй строки “ ³ полусуммы соответствующих элементов первой и третьей строк. Кроме того, элементы третьего столбца матрицы А2 “ ³“ соответствующих элементов второго столбца. Применяя свойство 5 получим, что всякое решение игры 3 = (Х 4,2, 1,4, А2) является решением игры 2, а следовательно и игры 1. Игра 3 определяется матрицей
.
Матрица А3 не имеет седловой точки, т.к. не выполнено равенство
= ,
а игра 3 не имеет решения в чистых стратегиях, т.е. оптимальные стратегии игроков являются смешанными. Эти стратегии (в данном случае) легко найти из анализа структуры матрицы А3. Поскольку матрица А3 симметрична, можно предположить, что игроки в оптимальной стратегии используют свои чистые стратегии с равными вероятностями.
Действительно, если игрок 1 выбирает с равными вероятностями стратегии 1 и 3, то при применении любой из двух чистых стратегий игроком 2 математическое ожидание выигрыша игрока 1 будет равным либо
,
либо
.
Аналогично, если игрок 2 использует свои чистые стратегии 2 и 3 с равными вероятностями, то математическое ожидание его проигрыша будет равно 
. Следовательно, указанные стратегии являются оптимальными в игре 3, а величины значением игры 3. Из предыдущего следует, что эти стратегии оптимальны и в 1.
Таким образом, стратегия Х = (
, 0, , 0) является оптимальной стратегией игрока 1, стратегия = (0, , , 0) оптимальной стратегией игрока 2 в игре 1, а значение игры 1 равно . В силу свойства 4 решением игры будет тройка (Х,, 
).
ИГРЫ ПОРЯДКА 2 х2.
В общем случае игра 2 2 определяется матрицей
Прежде всего необходимо проверить, есть ли у данной игры седловая точка. Если да, то игра имеет решение в чистых стратегиях, причём оптимальными стратегиями игроков 1 и 2 соответственно будут чистая максиминная и чистая минимаксная стратегии. Если же игра с матрицей выигрышей А не имеет чистых стратегий, то оба игрока имеют только такие оптимальные стратегии, которые используют все свои чистые стратегии с положительными вероятностями. В противном случае один из игроков (например 1) имеет чистую оптимальную стратегию, а другой только смешанные. Не ограничивая общности, можно считать, что оптимальной стратегией игрока 1 является выбор с вероятностью 1 первой строки. Далее, по свойству 1 следует, что а11 = а12 = u и матрица имеет вид
.
Легко видеть, что для матриц такого вида одна из стратегий игрока 2 является доминируемой. Следовательно, по свойству 4 этот игрок имеет чистую стратегию, что противоречит предположению.
Пусть Х = (x, 1 - x) оптимальная стратегия игрока 1. Так как игрок 2 имеет смешанную оптимальную стратегию, из свойства 1 получим, что (см. также свойство 7)
Отсюда следует, что при u ¹ 0 столбцы матрицы А не могут быть пропорциональны с коэффициентом пропорциональности, отличным от единицы. Если же коэффициент пропорциональности равен единице, то матрица А принимает вид
и игрок 1 имеет чистую оптимальную стратегию (он выбирает с вероятностью 1 ту из строк, элементы которой не меньше соответствующих элементов другой), что противоречит предположению. Следовательно, если u ¹ 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы А отличен от нуля. Из этого следует, что последняя система уравнений имеет единственное решение. Решая её, находим
;
.
Аналогичные рассуждения приводят нас к тому, что оптимальная стратегия игрока 2 = (h, 1 - h) удовлетворяет системе уравнений
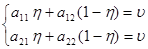
откуда
.
