Игры с выпуклыми непрерывными функциями выигрышей, называемые часто ядром, называются выпуклыми.
Напомним, что выпуклой функцией f действительной переменной х на интервале (а,b) называется такая функция, для которой выполняется неравенство
f (a1 х1 + a2 х2) £ a1 f (х1) + a2 f (х2),
где х1 и х2 любые две точки из интервала (а,b); a1, a2 ³ 0, причём a1 + a2 = 1.
Если для a1 ¹ 0, a2 ¹ 0 всегда имеет место строгое неравенство
f (a1 х1 + a2 х2) < a1 f (х1) + a2 f (х2),
то функция f называется строго выпуклой на (а;b). Геометрически выпуклая функция изображает дугу, график которой расположен ниже стягивающей её хорды (см. рис.)
Напомним, также, что непрерывная и строго выпуклая функция f на замкнутом интервале принимает минимальное значение только в одной точке интервала.
Для нахождения решения выпуклой игры можно воспользоваться следующей теоремой.
Теорема 4. Пусть М (х, y) непрерывная функция выигрышей игрока 1, на единичном квадрате и строго выпуклая по y для любого х. Тогда имеется единственная оптимальная чистая стратегия y = yo Î[0;1] для игрока 2, цена игры определяется по формуле
V = 
M (x, y), 
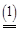
значение yo определяется как решение следующего уравнения
M (x, yo) = V. 
Замечание. Если в теореме 4 не предполагать строгую выпуклость функции М (х, y) по y, а просто выпуклость, то теорема остаётся в силе с тем отличием, что у игрока 2 оптимальная чистая стратегия не будет единственной.
Замечание. Выпуклые игры называют часто выпукло-вогнутыми, т.к. игра в них имеет седлообразное ядро, а так как ядро седлообразное, то игра имеет седловую точку в чистых стратегиях.
Таким образом, если М (х, y) непрерывна и выпукла по y, то цена игры определяется по формуле (1), и игрок 2 имеет оптимальную чистую стратегию, определяемую из уравнения (2).
Аналогично и для игрока 1: если функция выигрышей М (х, y) непрерывна по обоим аргументам и строго вогнута по х при любом y, то в этом случае игрок 1 имеет единственную оптимальную стратегию.
Цена игры определяется по формуле
V = M(x,y), 
а чистая оптимальная стратегия хo игрока 1 определяется из уравнения
M (xo, y) = V. 
Пример. Пусть на квадрате [0;1] задана функция
М (х, y) = 
. 
Так как
для x Î[0; 1], y Î(0;1),
то М (х, y) строго вогнута по х для любого y Î(0;1). Следовательно, цена игры находится по формуле (3)
V = .
Отметим, что при 0 £ х £ 
справедливо равенство
= 
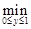
а при 0,5 < х £ 1
= 
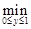
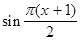
Поэтому
V = max [ 
; 
] =
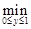
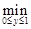
= max [ ; ] =
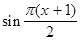= max [ 
; ] = .
При этом значение х получается равным хo = . Это же значение получается из решения уравнения
= ,
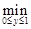
т.к. минимум достигается при y = 0, и это уравнение превращается в следующее
= ,
откуда следует, что х = .
Заметим, что если в функции выигрышей (5) поменять местами х и y, то она не изменится, а следовательно, эта функция выпукла и по y при всех х Î[0;1]. Поэтому к ней применима та же теория, т.е. у игрока 2 существует оптимальная чистая стратегия yo, определяемая из уравнения (4)
=
Очевидно, максимум по х достигается при х = , и последнее уравнение примет вид
= .
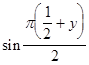Решением последнего уравнения будет yo = 0. Следовательно, игрок 2 имеет оптимальную чистую стратегию yo = 0.
Замечание. В приведённом выше примере мы могли определить оптимальную стратегию игрока 1, а игрока 2 - только случайно, в силу удачного вида М (х, y).
Рассмотрим теперь метод определения оптимальных стратегий того игрока, для которого функция выигрышей не обязательно выпукла. Пусть непрерывная функция М (х, y), заданная на единичном квадрате, выпукла по y. Нас будет интересовать вопрос нахождения оптимальных стратегий 1 игрока. Предположим также, что для х Î[0; 1], y Î[0; 1] существует частная производная функции М (х, y) по y, причём в точках y = 0 и y = 1 
(х, y) = 
понимается как правая и левая производная соответственно. Обозначим через yo одну из оптимальных чистых стратегий игрока 2 (эта стратегия существует в соответствии с теоремой 4).
Согласно теореме 2 чистые стратегии х игрока 1 могут входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство
М (х, yo) = V.
Такие чистые стратегии х называются существенными.
Теорема 5. Пусть дана бесконечная антагонистическая игра с непрерывной и дифференцируемой по y на единичном квадрате при любом х функцией выигрышей М (х, y), с оптимальной чистой стратегией yo игрока 2 и ценой игры V, тогда:
1) если yo = 1, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х1, для которой
(х1, 1) £ 1;
2) если yo = 0, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х2, для которой
(х2, 0) ³ 0;
3) если 0 £ yo £ 1, то среди оптимальных стратегий игрока 1 найдётся такая, которая является смесью двух существенных стратегий х1 и х2. Для этих стратегий
(х1, yo) £ 0, (х2, yo) ³ 0,
стратегия х1 употребляется с вероятностью a, стратегия х2 с вероятностью (1 - a), где a находится из уравнения
a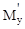 
(х1, yo) + (1 - a) 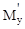(х2, yo) = 0. 
Пример. Пусть функция выигрышей в бесконечной антагонистической игре задана на единичном квадрате и равна
М (х, y) = (х - y)2 = х2 - 2хy + y2.
Эта функция непрерывна по х и y, и поэтому эта игра имеет решение. Кроме того
= 2 > 0.
Следовательно, М (х, y) выпукла по y, и поэтому согласно теореме 4 цена игры определяется по формуле (1), игрок 2 имеет чистую оптимальную стратегию yo, определяемую из уравнения (2). Таким образом, имеем
V = (x - y)2;
Для определения (x2 - 2xy + y2) последовательно найдём
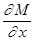= 2x - 2 y:= 0 Þ x = y
= 2 > 0 Þ при x = y функция M имеет минимум для любого y.
Þ максимум достигается в одной из крайних точек x = 0 и (или) x = 1
M (0; y) = y2
M (1; y) = 1 - 2 y + y2 = (y - 1)2
Þ V= 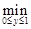max { y2; (1 - y)2}
Данный 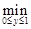max {...} достигается в том случае, если y2 = (1 - y)2, т.е. y = .
Следовательно V = 
при yo = .
Определим теперь оптимальные стратегии для игрока 1. Поскольку yo = , то 0 < yo < 1. Согласно теореме 5 рассмотрим третий случай.
Определим х из уравнения
М (х, yo) = V,
то есть
(х - )2 = .
Решая последнее уравнение, получим х1 = 0, х2 = 1. Теперь необходимо определить величину a вероятность применения чистой стратегии х1 = 0. С этой целью используем уравнение (*).
a (0, ) + (1 - a) (1, ) = 0.
Нетрудно найти
Тогда уравнение для a примет вид:
a - (1 - a) = 0,
откуда a = . Следовательно, стратегия игрока 1
F (х) = Jo (х) + J1 (х),
а игрока 2
Q (y) = 
(y).
Здесь через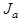 
(x) обозначена ступенчатая функция
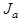(x) =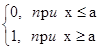 
.
