Определение бесконечной антагонистической игры

 

Естественным обобщением матричных игр являются бесконечные антагонистические игры (БАИ), в которых хотя бы один из игроков имеет бесконечное количество возможных стратегий. Мы будем рассматривать игры двух игроков, делающих по одному ходу, и после этого происходит распределение выигрышей. При формализации реальной ситуации с бесконечным числом выборов можно каждую стратегию сопоставить определённому числу из единичного интервала, т.к. всегда можно простым преобразованием любой интервал перевести в единичный и наоборот.

Напоминание. Пусть Е  некоторое множество вещественных чисел. Если существует число y, такое, что x £ y при всех хÎЕ (при этом y не обязательно принадлежит Е), то множество Е называется ограниченным сверху, а число y называется верхней границей множества Е. Аналогично определяется ограниченность снизу и нижняя граница множества Е. Обозначаются верхняя и нижняя границы соответственно через sup Е и inf Е соответственно.

 

Пример. Пусть множество Е состоит из всех чисел вида , n = 1,2,... Тогда множество Е ограничено, его верхняя грань равна 1, а нижняя 0, причём 0Ï Е, а 1Î Е.

Для дальнейшего изложения теории игр этого класса введём определения и обозначения: [0; 1]  единичный промежуток, из которого игрок может сделать выбор; х  число (стратегия), выбираемое игроком 1; y  число (стратегия), выбираемое игроком 2; М_i(x,y)  выигрыш i -го игрока; G (X,Y,M₁,M₂)  игра двух игроков, с ненулевой суммой, в которой игрок 1 выбирает число х из множества Х, игрок 2 выбирает число y из множества Y, и после этого игроки 1 и 2 получают соответственно выигрыши M₁ (x, y) и M₂ (x, y). Пусть, далее, G (X,Y,M)  игра двух игроков с нулевой суммой, в которой игрок 1 выбирает число х, игрок 2  число y, после чего игрок 1 получает выигрыш М (x, y) за счёт второго игрока.

Большое значение в теории БАИ имеет вид функции выигрышей M (x, y). Так, в отличии от матричных игр, не для всякой функции M (x, y) существует решение. Будем считать, что выбор определённого числа игроком означает применение его чистой стратегии, соответствующей этому числу. По аналогии с матричными играми назовём чистой нижней ценой игры величину

V₁ = M (x, y) или V₁ = M (x, y),

а чистой верхней ценой игры величину

V₂ = M (x, y) или V₂ = M (x, y),

Для матричных игр величины V₁ и V₂ всегда существуют, а в бесконечных играх они могут не существовать.

Естественно считать, что, если для какой-либо бесконечной игры величины V₁ и V₂ существуют и равны между собой (V₁ = V₂ = V), то такая игра имеет решение в чистых стратегиях, т.е. оптимальной стратегией игрока 1 есть выбор числа x_oÎX и игрока 2  числа y_oÎY, при которых M(x_o, y_o) = V, в этом случае V называется ценой игры, а (x_o, y_o)  седловой точкой в чистых стратегиях.

 

Пример 1. Игрок 1 выбирает число х из множества Х = [0; 1], игрок 2 выбирает число y из множества Y = [0; 1]. После этого игрок 2 платит игроку 1 сумму

M (x, y) = 2х² - y².

Поскольку игрок 2 хочет минимизировать выигрыш игрока 1, то он определяет

(2x² - y²) = 2х² - 1,

т.е. при этом y = 1. Игрок 1 желает максимизировать свой выигрыш, и поэтому определяет

( M (x, y)) = (2х² - 1) = 2-1 = 1,

который достигается при х = 1.

Итак, нижняя цена игры равна V₁ = 1. Верхняя цена игры

V₂ = ( (2х² - y²)) = (2 - y²) = 2-1 = 1,

т.е. в этой игре V₁ = V₂ = 1. Поэтому цена игры V = 1, а седловая точка (1;1).

 

Пример 2. Игрок 1 выбирает хÎX = (0; 1), игрок 2 выбирает yÎY = (0; 1). После этого игрок 1 получает сумму

M (x, y) = x + y

за счёт игрока 2. Поскольку Х и Y - открытые интервалы, то на них V₁ и V₂ не существуют. Если бы Х и Y были замкнутые интервалы, то, очевидно, было бы следующее:

V₁ = V₂ = 1 при x_o = 1, y_o = 0.

С другой стороны, ясно, что, выбирая х достаточно близкое к 1, игрок 1 будет уверен, что он получит выигрыш не меньше, чем число, близкое к цене игры V = 1; выбирая y близкое к нулю, игрок 2 не допустит, чтобы выигрыш игрока 1 значительно отличался от цены игры V = 1.

 

 

Степень близости к цене игры может характеризоваться числом e > 0. Поэтому в описываемой игре можно говорить об оптимальности чистых стратегий х_o = 1, y_o = 0 соответственно игроков 1 и 2 с точностью до произвольного числа e > 0. В связи с этим введём следующие определения.

Точка (, ), где ÎX, ÎY, в антагонистической непрерывной игре G называется точкой e-равновесия, если для любых стратегий xÎX игрока 1, yÎY игрока 2 имеет место неравенство

М (х, ) - e £ M (, ) £ М(, y) + e.

Точка e-равновесия (, ) называется также e-седловой точкой функции М (x, y), а стратегии и называются e- оптимальными стратегиями. Эти стратегии являются оптимальными с точностью до e в том смысле, что, если отклонение от оптимальной стратегии никакой пользы игроку принести не может, то его отклонение от e-оптимальной стратегии может увеличить его выигрыш не более, чем на e.

Можно доказать, что для того, чтобы функция М имела e-седловые точки для любого e > 0 необходимо и достаточно чтобы

M (x, y) = M (x, y).

Если игра G не имеет седловой точки (e-седловой точки) в чистых стратегиях, то оптимальные стратегии можно искать среди смешанных стратегий. Однако, в качестве вероятностной меры здесь вводятся функции распределения вероятностей применения игроками чистых стратегий.

Пусть F (х)  функция распределения вероятностей применения чистых стратегий игроком 1. Если число x - чистая стратегия игрока 1, то

F (х) = P (x £ х),

где P (x £ х) означает вероятность того, что случайно выбранная чистая стратегия x не будет превосходить числа х. Аналогично рассматривается функция распределения вероятностей применения чистых стратегий h игроком 2

Q (y) = P (h £ y).

Функции F (х) и Q (y) называются смешанными стратегиями соответственно игроков 1 и 2. Если F (х) и Q (y) дифференцируемы, то существуют их производные, обозначаемые соответственно через f (x) и q (y) (функции плотности распределения).

В общем случае дифференциал функции распределения dF (х) выражает вероятность того, что стратегия x находится в промежутке

х £ x £ х + dх.

Аналогично для игрока 2: dQ (y) означает вероятность того, что его стратегия h находится в интервале

y £ h £ y + dy.

Тогда выигрыш игрока 1 составит

М (х, y) dF (х),

а выигрыш игрока 2 равен

М (х, y) dQ (y).

Средний выигрыш игрока 1 при условии, что игрок 2 применяет свою чистую стратегию y, получим, если проинтегрируем выигрыш по всем возможным значениям х, т.е.

E (F, y) =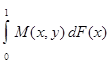

Напомним, что множество Y для y является замкнутым промежутком [0; 1].

Если игрок 1 применяет свою чистую стратегию х, а игрок 2 - y, то выигрыш игрока 1 составит

М (х, y) dP (х) dQ (y).

Средний выигрыш игрока 1 при условии, что оба игрока применяют свои смешанные стратегии F (х) и Q (y), будет равен

E (F,Q) = .

По аналогии с матричными играми определяются оптимальные смешанные стратегии игроков и цена игры: в антагонистической непрерывной игре G (Х,Y,М) пара смешанных стратегий F* (х) и Q* (y) соответственно для игроков 1 и 2 образует седловую точку в смешанных стратегиях, если для любых смешанных стратегий F (х) и Q (y) справедливы соотношения

Е (F,Q*) £ Е (F*,Q*) £ Е (F*,Q).

Из левой части последнего неравенства следует, что если игрок 1 отступает от своей стратегии F* (х), то его средний выигрыш не может увеличиться, но может уменьшиться за счёт лучших действий игрока 2, поэтому F* (х) называется оптимальной смешанной стратегией игрока 1.

Из правой части последнего неравенства следует, что если игрок 2 отступит от своей смешанной стратегии Q* (y), то средний выигрыш игрока 1 может увеличиться, а не уменьшиться, за счёт более разумных действий игрока 1, поэтому Q* (y) называется оптимальной смешанной стратегией игрока 2. Средний выигрыш Е (F*,Q*), получаемый игроком 1 при применении игроками оптимальных смешанных стратегий, называется ценой игры.

По аналогии с матричными играми рассматривается нижняя цена непрерывной игры в смешанных стратегиях

V₁ = 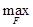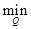E (F,Q)

и верхняя цена игры

V₂ = E (F,Q).

Если существуют такие смешанные стратегии F* (х) и Q* (y) соответственно для игроков 1 и 2, при которых нижняя и верхняя цены непрерывной игры совпадают, то F* (х) и Q* (y) естественно назвать оптимальными смешанными стратегиями соответствующих игроков, а V₁ = V₂ = V  ценой игры.

Можно доказать, что существование седловой точки в смешанных стратегиях игры G (Х,Y,М) равносильно существованию верхней V₂ и нижней V₁ цен игры в смешанных стратегиях и их равенству V₁ = V₂ = V.

Таким образом, решить игру G (Х,Y,М)  означает найти седловую точку или такие смешанные стратегии, при которых нижняя и верхняя цены игры совпадают.

 

Теорема 1 (существования). Всякая антагонистическая бесконечная игра двух игроков G с непрерывной функцией выигрышей М (х,y) на единичном квадрате имеет решение (игроки имеют оптимальные смешанные стратегии).

 

Теорема 2. Пусть  бесконечная антагонистическая игра с непрерывной функцией выигрышей М (х, y) на единичном квадрате и ценой игры V. Тогда, если Q (y)  оптимальная стратегия игрока 2 и для некоторого x_o

,

то x_o не может входить в точки спектра оптимальной стратегии игрока 1; если F (х)  оптимальная стратегия игрока 1и для некоторого y_o

,

то y_o не может быть точкой спектра оптимальной стратегии игрока 2.

Из теоремы 2 следует, что если один из игроков применяет оптимальную стратегию, а другой  чистую, притом что средний выигрыш игрока 1 отличается от цены игры, то эта чистая стратегия не может войти в его оптимальную стратегию (или она входит в неё с вероятностью нуль).

 

Теорема 3. Пусть в бесконечной антагонистической игре функция выигрышей М (х,y) непрерывная для х Î[0; 1], y Î[0; 1] и

М (х, y) = -М (y, х),

тогда цена игры равна нулю и любая оптимальная стратегия одного игрока будет также оптимальной стратегией другого игрока.

Сформулированные свойства оптимальных смешанных стратегий и цены игры помогают находить или проверять решения, но они ещё не дают в общем виде приемлемых методов решения игры. Более того, не существует общих методов для точного нахождения решения БАИ, и в том числе непрерывных игр на единичном квадрате. Поэтому рассматриваются частные виды антагонистических бесконечных игр.