План
1.НСД і НСК елементів кільця P[x]. Лінійне представлення НСД елементів кільця P[x].
2.Незвідні многочлени.
3.Канонічний розклад многочлена.
1. НСД і НСК елементів кільця P[x].
Означення 1:Якщо многочлен d(x) є дільником многочлена f(x) і многочлена g(x),то він називається спільним дільником многочленів f(x) і g(x).
Означення2:Спільний дільник многочленів f(x) і g(x),який ділиться на кожний інший спільний дільник цих многочленів,називається НСД многочленів f(x) і g(x) і позначається – (f,g).
! Якщо d(x) – найбільший спільний дільник (f(x) і g(x),то й кожний многочлен сd(x),де с – елемент поля Р,відмінний від нуля,також є НСД цих многочленів.
! З точністю до сталого множника НСД визначається одночасно.
О3:Многочлени f(x),g(x) є P[x] називається взаємно-простими,якщо кожний їхній спільний дільник є многочленом нульового елемента (відмінною від нуля константою)
Теорема 1:Для будь-яких двох многочленів f(x) і g(x) є P[x] існує найбільший спільний дільник d(x),причому d(x) можна подати у вигляді
d(x)=f(x)u(x)+g(x)v(x),
де u(x) і v(x) – деякі многочлени з P[x].
Спосіб знаходження НСД двох многочленів – алгоритм Євкліда.
Нехай дано два многочлена g(x) i f(x),причому степінь f(x) не менший g(x). Виконаємо послідовне ділення з остачею,яке можна записати за допомогою такої системи рівностей:
f(x)=g(x)  (x)+
(x)+  (x),
(x),
g(x)=  (x)
(x)  (x)+
(x)+ 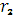 (x),
(x),
 (x)=
(x)= 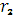 (x)
(x)  (x)+
(x)+  (x), (1)
(x), (1)
………………………
 (x)=
(x)=  (x)
(x)  (x)+
(x)+  (x),
(x),
 (x)=
(x)= 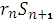 (x).
(x).
Після скінченного числа ділень остача  (x)=0.
(x)=0.
deg  (x)<deg g(x), deg
(x)<deg g(x), deg 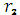 (x)< deg
(x)< deg  (x) і.т. степінь deg
(x) і.т. степінь deg 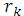 (x)<deg
(x)<deg 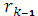 (x). Це означає,що або якась з остач
(x). Це означає,що або якась з остач 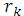 (x) дорівнюватиме нулю,або степінь остачі,зменшуючись при кожному ділення принаймні на 1 дорівнюватиме 0.
(x) дорівнюватиме нулю,або степінь остачі,зменшуючись при кожному ділення принаймні на 1 дорівнюватиме 0.
Якщо deg  (x)=0,то
(x)=0,то  =0,бо будь-який многочлен ділиться на многочлен нульового степеня.
=0,бо будь-який многочлен ділиться на многочлен нульового степеня.
Оскільки степінь  (x)
(x) 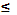 m-1,де m – степінь g(x),то число кроків у схемі (1) не може перевищувати m.
m-1,де m – степінь g(x),то число кроків у схемі (1) не може перевищувати m.
Приклад 1. Нехай f(x)= 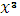 -3
-3 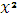 +3x-1, g(x)=-1.Застосуємо алгоритм Євкліда.
+3x-1, g(x)=-1.Застосуємо алгоритм Євкліда.






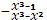
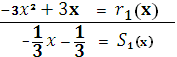

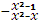



0 (f,g)=x-1
Лінійне представлення НСД
Оскільки d(x)= 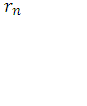 (x),то з рівностей (1) дістаємо
(x),то з рівностей (1) дістаємо
d=  -
- 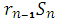 . (2)
. (2)
У свою чергу
 -
- 
 -
- 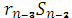 (3)
(3)
………………………...
 -
-  . (4)
. (4)
Підставляючи у (2) вираз (3) дістанемо:
d=  - (
- ( - (
- ( -
- 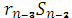 )
) 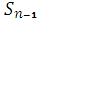 )
) 
d= 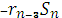 +
+  (1+
(1+ 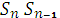 )
) 
Виключаючи далі  ,…,ми щоразу діставатимемо вираз d через
,…,ми щоразу діставатимемо вираз d через  i
i  ,в якому множники утворені з часток
,в якому множники утворені з часток  за допомогою додавання і множення. Процес поступового виключення
за допомогою додавання і множення. Процес поступового виключення  припиниться тоді,коли в правій частині рівності з’явиться
припиниться тоді,коли в правій частині рівності з’явиться  i
i 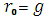 .
.
Отже дістанемо
d=fu+gv (5)
Приклад 2: З прикладу 1
d=  =x-1
=x-1
 (x)=
(x)= 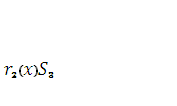 (x)+f(x)=
(x)+f(x)=  (x)
(x)
g(x)=  (x)
(x)
Означення 4. Спільним кратним многочленів f(x), g(x) є P[x] називається будь-який многочлен S(x) є P[x] такий, що S(x): f(x) і S(x): g(x). Найменшим спільним кратним (НСК) многочленів f(x) і g(x) називається спільне кратне f(x) і g(x),яке ділить будь-яке інше спільне кратне цих многочленів. НСК многочленів f(x) і g(x) позначають [f,g].
Теорема 3. Для будь-яких відмінних від нуля многочленів f(x) і g(x) найменше спільне кратне існує і визначається однозначно з точністю до сталого множника

r2(x) = g(x) – r1(x) S2(x)
r2(x) = g(x) – (f(x) – g(x) S1(x)) S2(x)
r2(x) = g(x) – f(x) S2(x) + g (S1(x) S2(x)) = g(x) (1 + S1(x) S2(x)) – f(x) S2(x)
r2(x) = (x3 – 1) (1 + (-  x -
x -  ) – (x3 – 3x2 + 3x + 1) (-
) – (x3 – 3x2 + 3x + 1) (-  x -
x -  )
)
V(x) = ( -
-  x), U(x) = (
x), U(x) = ( x -
x -  )
)
НСК = -4(а)
2. Незвідні многочлени.
Означення 1. Многочлен f(x) є P[x] називається незвідним у полі Р, якщо він не є константа і не має дільників, відмінних від константи і від многочленів виду c f(x), де с – константа.
Означення 2. Многочлен f(x) є P[x] називається звідним у полі Р, коли
deg f ≥1 і коли існують такі многочлени g(x), S(x) є P[x], що f(x) = g(x) S(x) є P[x], причому deg g ≥1, deg S ≥1.
Звідність чи незвідність многочлена є поняття відносне і залежить від поля Р, над яким многочлен розглядається.
Приклад 3. Многочлен (х2 + 1) незвідний у полі раціональних чисел і в полі дійсних чисел. Він звідний в полі комплексних чисел.
Приклад 4. Многочлен (х2 - 2) незвідний у полі раціональних чисел. Він звідний у полі чисел виду а + b  (a, b є Q): (х2 - 2) = (х -
(a, b є Q): (х2 - 2) = (х -  ) (х +
) (х +  )
)
Теорема 2. Многочлен першого степеня над довільним полем Р незвідний у цьому полі.
3. Канонічний розклад многочлена
Теорема 3. Кожний многочлен f(x) ненульового степеня над полем Р можна подати у вигляді:
f(x) = p1(x) p2(x) … pl(x), (6)
де всі pk(x) є незвідними многочленами у полі Р. Зображення (6) єдине з точністю до сталих множників і до порядку нумерації многочленів pk(x).
Наслідок. Довільний многочлен ненульового степеня над полем Р можна подати у вигляді:
f(x) = [p1(x)]k1 [p2(x)]k2 … [pm(x)]km (7)
Зображення (7) – канонічний розклад многочлена f(x) у полі Р.
Означення 3. Якщо многочлен pi(x) входить у канонічний розклад (7) у степені з показником kj, кажуть, що pj(x) є множником кратності kj многочлена f(x). Множники кратності яких більша за одиницю називаються кратними множниками многочлена.
Приклад 5. Розкладемо f(x) = х3 + х2 – 5х + 3 на незвідні множники в полі раціональних чисел:
f(x) = х3 + х2 – 5х + 3 = (х – 1) (х – 1) (х +3) = (х – 1)2(х + 3)
p1(x) = x – 1 – кратності 2.
P2(x) = x + 3 – кратності 1.
Такий розклад у будь-якому полі, бо це многочлени 1-го степеня.
Приклад 6. f(x) = х4 – х2 + 4 = (х2 – 2) – у полі раціональних чисел.
f(x) = (х -  ) (х +
) (х +  ) – у полі дійсних чисел. Обидва множники кратності 2.
) – у полі дійсних чисел. Обидва множники кратності 2.
Теорема 4. Якщо многочлени f(x) і g(x) розкладені на незвідні множники у довільному полі Р, то НСД (f,g) дорівнює добутку всіх незвідних множників, які входять у розклад як f(x) так і g(x). Якщо таких спільних незвідних множників немає, то (f,g) = 1.
Приклад 7. Нехай f(x) = (х – 1)2(х + 3), g(x) = (х – 1)3. НСД (f,g) = (х – 1)2, тобто (f,g) = х2 – 2х +1
****************************************************************************
Лекція 3
Корені многочлена
План
1. Означення і ознака кореня многочлена. Кратні корені.
2. Теорема про найбільшу можливу кількість коренів многочлена.
3. Існування кореня многочлена над довільним полем. Формули Вієта.
4. Про алгебраїчну і функціональну рівність многочленів. Приклади.






