План
1. Кільце многочленів К[x].
2. Подільність в К[x].Теорема про ділення з остачею в К[x], де К – поле.
3. Ділення многочлена на лінійний двочлен. Схема Горнера. Теорема Безу. Розклад многочлена за степенями лінійного двочлена.
1. Кільце многочленів К[x].
З курсу математичного аналізу відомо,що многочленом від однієї змінної є ціла раціональна функція виду:
 (1)
(1)
задана на множині дійсних чисел,де коефіцієнти  – довільні задані дійсні числа.
– довільні задані дійсні числа.
Найпростіші типи многочленів лінійна функція  та квадратний тричлен
та квадратний тричлен  відомі зі школи.
відомі зі школи.
В алгебрі многочлени зустрічались у зв’язку з розв’язуванням алгебраїчних рівнянь вищих степенів з одним невідомим,тобто рівнянь виду:
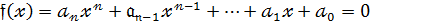 (2)
(2)
ліва частина яких є многочлен від однієї змінної. На відміну від аналізу в алгебрі многочлени вважалися цілими раціональними функціями комплексної змінної,тобто виразами виду (1),в яких коефіцієнти  є комплексні числа,а змінна
є комплексні числа,а змінна  може набувати довільних комплексних значень. Це важливо для розв’язування рівнянь 3-го,4-го і вищих степенів.
може набувати довільних комплексних значень. Це важливо для розв’язування рівнянь 3-го,4-го і вищих степенів.
Означення многочлена
Вираз виду:

Повністю визначається коефіцієнтами  .
.
Їх вибирають так щоб над ними можна було виконувати операції додавання та множення за тими правилами,що і в елементарній математиці, і ці дії мали властивості:
· Асоціативність;
· Дистрибутивність;
· Комутативність.
Коефіцієнти многочленів повинні належати деякому комутативному кільцю К,без дільників нуля ( ) – області цілісності К.
) – області цілісності К.
Означення 1.
Многочленом(поліномом)від однієї змінної над областю цілісності К називається вираз виду (3), де  довільне ціле невід’ємне число
довільне ціле невід’ємне число  - елементи К, а
- елементи К, а  деякі символи;
деякі символи;  називається
називається  степенем змінної
степенем змінної  (або невідомого
(або невідомого  ), а
), а  м коефіцієнтом многочлена (3) або коефіцієнтом при
м коефіцієнтом многочлена (3) або коефіцієнтом при  (
( .
.
Многочлени від однієї змінної  позначатимемо:
позначатимемо:  . Сукупність всіх многочленів від
. Сукупність всіх многочленів від  над областю цілісності К-символом К[
над областю цілісності К-символом К[  ].
].
Означення 2.
Вираз  називається
називається  членом або членом
членом або членом  го степеня многочлена.
го степеня многочлена.
 (4)
(4)
 нульовим або вільним членом причому записи
нульовим або вільним членом причому записи  рівнозначні. Якщо
рівнозначні. Якщо  (тобто є нульовим елементом області цілісності К),то кажуть,що
(тобто є нульовим елементом області цілісності К),то кажуть,що  член многочлена
член многочлена  дорівнює нулю або його немає.
дорівнює нулю або його немає.
У виразі для многочлена (4) члени, які дорівнюють нулю можна не писати. Так многочлен:
 (5)
(5)
Можна записати коротше:

Означення 3.
Відмінний від нуля член многочлена  ,степінь якого більший за степінь усіх інших відмінних від нуля членів цього многочлена,називається старшим членом, його коефіцієнт старшим коефіцієнтом, а його степінь – степенем многочлена
,степінь якого більший за степінь усіх інших відмінних від нуля членів цього многочлена,називається старшим членом, його коефіцієнт старшим коефіцієнтом, а його степінь – степенем многочлена  .
.
Степінь многочлена  позначають deg f.
позначають deg f.
Будь-який многочлен  записуватимемо так,щоб запис починався зі старшого члена,тобто не включати у запис рівних нулю членів,степінь яких більший за deg f. Так многочлен (6) подаватимемо у будь-якому з виглядів:
записуватимемо так,щоб запис починався зі старшого члена,тобто не включати у запис рівних нулю членів,степінь яких більший за deg f. Так многочлен (6) подаватимемо у будь-якому з виглядів:


Будь - який многочлен  степеня подаватимемо у вигляді:
степеня подаватимемо у вигляді:
 (7)
(7)
де  ,а з решти коефіцієнтів частина або всі можуть дорівнювати нулю.
,а з решти коефіцієнтів частина або всі можуть дорівнювати нулю.
Таку форму запису називають канонічною. Вживають також назву «многочлен стандартного виду».
 - лінійний двочлен.
- лінійний двочлен.
Многочлени нульового степеня вважають константами,цей многочлен називатимемо нуль многочленом:  .
.
Нуль – многочлен немає ніякого степеня.
Дії над многочленами.
Нехай дано два многочлени над областю цілісності R.

( К,
К,  (8)
(8)

( ) (9)
) (9)
Означення 1.
Многочлени  називають рівними між собою і записують
називають рівними між собою і записують 
 , якщо канонічні формицих многочленів збігається,тобто
, якщо канонічні формицих многочленів збігається,тобто

 (10)
(10)
Рівність многочленів має властивості рефлексивності,симетричності та транзитивності,тобто є відношенням еквівалентності на множині К[x].
Означення 2.
Сумою многочленів  називається многочлен:
називається многочлен:
 (11).
(11).
Те,що  є сумою многочленів
є сумою многочленів 
 записують так:
записують так:

Н1.
Якщо  є К[
є К[  ],
], 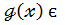 К[
К[  ], то й
], то й 
Н2.
Степінь суми двох многочленів не перевищує більшого зі степенів даних многочленів:
deg 
Н3.
Для довільного многочлена  К[
К[  ] і
] і 
 К[
К[  ]
]
 (12)
(12)
Означення 3.
Добутком многочленів  (8 і 9) називається многочлен:
(8 і 9) називається многочлен:
 (13)
(13)
де
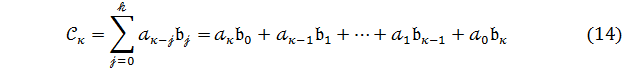
( ),
), 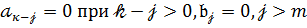
Те що  є добутком многочленів
є добутком многочленів  , записують так:
, записують так:
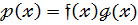 .
.
Наведене означення є безпосереднім узагальненням «шкільного» правила множення многочленів.
Вираз (14) можна переписати:


 .
.
Н4:
Якщо  є К[
є К[  ],
],  є К[
є К[  ],то й
],то й  є К[
є К[  ]
]
Н5:
Якщо  не є нуль-многочлени,то deg (
не є нуль-многочлени,то deg ( )=deg
)=deg  deg
deg  . (16)
. (16)
Н6:
При множені двох многочленів,з яких хоч один нуль-многочлен дістаємо нуль-многочлен.
 (17)
(17)
Теорема 1:
Сукупність К[  ] усіх многочленів над областю цілісності К є область цілісності відносно операції додавання та множення многочленів.
] усіх многочленів над областю цілісності К є область цілісності відносно операції додавання та множення многочленів.
Доведення:
З наслідків 1 та 4 випливає що сукупність К[  ] є комутативне кільце відносно заданих операцій:
] є комутативне кільце відносно заданих операцій:
1. 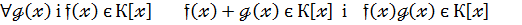
2.  тому, що
тому, що  є комутативне кільце і
є комутативне кільце і

3.Асоціативність додавання многочленів.
Розглянемо три многочлени:

[  ]+
]+  (18)
(18)
випливає безпосередньо з асоціативності додавання елементів у кільці К.
За означенням рівності многочленів співвідношення (18) рівносильне степені рівностей:
(
4.Нульовим елементом в  К[
К[  ] є очевидно нуль многочлен
] є очевидно нуль многочлен 

Існує в К[  ] протилежний
] протилежний
6.Для перевірки асоціативності множення многочленів:


Якщо  коефіцієнт многочлена
коефіцієнт многочлена  то відповідно до (15)
то відповідно до (15)

Але тоді  й коефіцієнт многочлена:
й коефіцієнт многочлена:
 є
є

З другого боку позначаючи через  й коефіцієнт многочлена
й коефіцієнт многочлена 
Дістаємо для 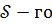 коефіцієнта многочлена
коефіцієнта многочлена  такий вираз:
такий вираз:

Зіставляючи (19) і (20) переконуємось що асоціативність виконується.
7.Дистрибутивний закон
[  ]
]  випливає з рівності
випливає з рівності

Отже К[  ] – комутативне кільце.
] – комутативне кільце.
Покажемо, що К[  ] – область цілісності, тобто не існує в ньому дільників нуля.
] – область цілісності, тобто не існує в ньому дільників нуля.
Нехай  є К[
є К[  ].
].
 старші коефіцієнти
старші коефіцієнти  .
.
 має старший коефіцієнт
має старший коефіцієнт  ,тому
,тому  не є нуль многочленом.
не є нуль многочленом.
Подільність в К[ ].
Слід показати,що для довільних многочленів 
 можна подати у вигляді:
можна подати у вигляді:
 (1)
(1)
Де  ,або deg
,або deg  Тут
Тут  ділене,
ділене,  дільник,
дільник,  частка,
частка, 
Степінь остачі повинен бути менший за степінь дільника.
Приклад 1: Нехай f(х)= х2-3х+1, g(х)=х2+1. Рівність х3-3х+1=(х2+1)х+(-4х+1) свідчить, що f(х) ÷ на g(х) з остачею. Частина S(х)=х, остача r(х) =-4х+1. Так само g(х ) ділитьсяна f(х) з остачею: х2+1=0 *( х3-3х+1)+х2+1. S1(х)=0 – частка, r1(х)=х2+1 – остача.
Теорема (про ділення з остачею в К[х]), де К -поле. Будемо вимагати, щоб К була полем, тобто, щоб в К існувала одиниця і для довільного елемента а≠0 існував обернений елемент а-1.
Сукупність всіх многочленів над полем Р є область цілісності з одиницею Р [х] відносно додавання і множення многочленів.
Теорема 1: Довільний многочлен f(х) з кільця Р[х] ділиться з остачею на будь-який многочлен g(х) з цього кільця, відмінний від 0 многочлена, при цьому частина й остача також належать до Р[х] і визначаються однозначно.
Доведення: Встановимо можливість знайти серед многочленів з кільця Р[х] частку S(х) і остачу r(х) для будь-яких многочленів f(х)= g(х) є Р[х] при g(х)≠0. Нехай f(х)= аnхn+an-1 xn-1+…+a1x+a0, g(х) = bmxm + bm-1xm-1+…+b1x+b0.
Якщо f(х)=0, то S(х)=0, r(х)=0. Нехай n=deg f(х)<deg g(x)=m тоді S(x)=0, r(x)=f(x). Розглянемо n≥m.
Виконаємо доведення методом індукції по n, починаючи з n=0. При n=0, m=0, f(x)=a0, g(x)=b0≠0 тому S(x)= a0/ b0, r(x)=0. S(x) є P(x), бо a0/b0 є Р.
Припустимо, що теорема справедлива для всіх многочленів таких, що deg f <n і доведемо її для многочленів степеня n.
Розглянемо многочлен
Р(х)=f(x)=an/bm xn-m g(x) an≠0, bm≠0.
Старший член многочлена аn/bm xn-m g(x)=anxn тобто старшому члену многочлена f(x). Тому deg P<n і за припущенням індукції Р(х) можна поділити з остачею на g(x);
P(x)= g(x)S1(x) + r1(x), S1(x), r1(x) є P[x], r1(x)=0 або deg r1<deg g.
Отже f(x)- an/bm xn-m g(x)= g(x)S1(x) + r1(x),
Звідси f(x)=g(x) S(x)+r(x), де r(x)=r1(x), S(x)=S1(x)+ an/bm xn-m, де S(x) і r(x) є P[x] і що r(x)=0, або deg r= deg r1<deg g.
Цим показано можливість ділення f(x) на g(x) з остачею. Встановимо єдиність частки S(x) і остачі r(x). Припустимо, що можливі два записи:
f(x)= g(x)S(x)+ r(x), deg r<deg g;
f(x)= g(x)S^(x)+r^(x), deg r^< deg g;
Віднімаючи другу рівність від першої, дістанемо:
g(x) [S(x)- S^(x)]=r(x)- r^(x). (2)
g(x)≠0 за умовою
Якщо припустити, що r(x) ≠ r^(x), то й S(x) ≠ S^(x) (адже Р[x] не має дільників нуля). Але приходимо до суперечливості. Справді права частина (2) є многочлен степінь якого менший від deg g і меншого від степеня лівої частини рівності (1). Отже (2) можлива коли коли r(x)= r^ (x) S(x)= S^(x), частка єдина, остача єдина. Теорема доведена.
4. Ділення многочлена на лінійний двочлен. Схема Горнера. Теорема Безу. Розклад многочлена за степенями лінійного двочлена. Практичне здійснення ділення з остачею, для двох заданихмногочленів ґрунтується на методі, використаному при доведенні теореми 1.
Приклад 1: Нехай f(x)=x4-2x3+x-1, a g(x)=x2-2
Знайдемо: g1(x)=f(x)- an/bm xn-m g(x):
g1(x)=x4-2x3+x-1-x2 (x2-2)=-2x3+2x2+x+1 далі з g1(x) так як з f(x);
g2(x)=-2x3+2x2+x-1+2x(x2-2)=2x2-3x-1;
g3(x)=2x2-3x-1-2(x2-2)=-3x+3
deg g3(x)<deg g(x) і тому S(x)=x2-2x+2, r(x)= -3x+3.
X4-2x3+x-1=(x2-2)(x2-2x+2)+ (-3x+3)
Це можна записати:
X4-2x3+x-1 x2-2
Метод невизначених коефіцієнтів
X4-2x3+x-1=(x2-2)S(x)+r(x) (3)
cтепінь S(x)≤n-m=2 r(x)<m, deg r(x)=1.
S(x)=A2x2+A1x+A0 r(x)=B1x+B0
Підставляючи вирази в рівність (3) маємо:
X4-2x3+x-1=(x2-2)(A2x2+A1x+A0)+(B1x+B0) на підставі означення рівності многочленів коефіцієнти при однакових степенях Х рівні між собою. Звідси дістанемо:
A2=1, A1=-2, -2A2+A0=0, -2A1+B1= 1, -2A0+B0=-1,
A2=1, A1=-2, A0=2, B1=-3, B0=3
S(x)=x2-2x+2, r(x)=-3x+3
У загальному випадку S(x) шукають у вигляді многочлена з невизначеними коефіцієнтами степеня n-m, a r(x)- m-1
Нехай g(x)= х-2 – лінійний двочлен. Використаємо метод невизначених коефіцієнтів
anxn+an-1xn-1+…+a1x+a0=(x- 2)(An-1xn-1+An-2xn-2+…+A1x+A0)+r. r-const. (4)
Прирівнюючи коефіцієнти у (4) дістанемо:
аn=An-1,
an-1=An-2- α An-1
……………………..
a1=A0- α A1,
a0= r- α A0,
звідси
An-1= an
An-2= an-1+ α An-1
An-3=an-2+ α A
……………………..
A0= a1+ α A1
r= a0+ α A0
Формули (5) показують, що поділити многочлен на х- α можна за такою схемою- схемою Горнера:
| аn | an-1 | an-2 | an-3 | … | a1 | a0 | |
| α | an An-1 | αAn-1+an-1 An-2 | αAn-2+an-2 An-3 | αAn-3+an-3 An-4 | … | αA1+a1 A0 | αA0+a0 r |
Виконуючи ділення з остачею за цією схемою, кожний наступний коефіцієнт Ак-1 частки й остачу r дістають множенням щойно обчисленого коефіцієнта Ак на α і додаванням до знайденого добутку відповідного коефіцієнта ак даного многочлена.
Приклад 2: Поділимо за схемою Горнера многочлен х4-3х2+2х-1 на х-2 а4=1, а3=0, а2=-3, а1=2, а0= -1, α=2.
| -3 | -1 | ||||
| 2*2-3=1 | 2*1+2=4 | 2*4-1=7 |
S(x)= x3+2x2+x+4, r=7
За схемою можна кілька раз ділити на один і той же лінійний двочлен
| -3 | -1 | ||||
Легко перевірити: остача при діленні f(x) на х- α дорівнює значенню многочлена при х= α тобто f(x). Це теорема Безу.
Т.Б для будь-якого елемента α з поля Р остача при діленні многочлена f(x) є P[x] на х- α= f(x).
Доведення: за формулою (1) ділення з остачею маємо:
f(x)=(х- α)S(x)+r, (6)
де многочлен r є константа, бо має степінь, нижчий від степеня х- α. Оскільки многочлени, що стоять у лівій і правій частинах (6) рівні між собою, то рівні між собою і їх значення при будь-якому х є Р. Тому взявши х= α, дістанемо f(α)=r, що й треба було довести.
За схемою Горнера зручно багато ділити многочлен на лінійний двочлен. За допомогою такого ділення легко дістати розклад довільного многочлена f(x) за степенями х- α.
Нехай f(x)- многочлен n-го степеня над полем Р, α-елемент цього поля. Ділення на х- α дає: f(x)=(х- α) f1(х)+С0, де (7)
f1(х)-многочлен (n-1)-го степеня з Р[x], a C0-елемент поля Р. Якщо n˃1 маємо:
f1(x)=(x- α) f2(x) + C1 (8)
f2(x)=(x- α)f3(x)+C2
……………………………
fn-1(x)= (x- α)fn(x)+Cn-1
fn(x) є многочлен нульового степеня fn(x)=Cn
Виключаючи з (7) і (8) fn-1(x),fn-2(x),…,f2(x), f1(x) дістанемо:
f(x)=Cn(x- α)n+Cn-1(x-α)n-1+…+C1(x-α)+C0 (9)
Отже, многочлен f(x) над полем Р ми подали як многочлен такого самого степеня над тим самим полем, але вже від заміненого у=х- α. При цьому коефіцієнти С0, С1, …Сn однозначно визначаються через α коефіцієнти а0, а1, …,аn многочлена f(х). А саме, С0 є остача від ділення f(х) першої частки f1(x) на х- α і т.д. Що ж до Cn то ще є остання частка в процесі послідовного ділення.
Приклад 4: Знайдемо розклад многочлена f(x)=х5-3х3+х2-2х+1 за степенями двочлена х-1.
| -3 | -2 | |||||
| -2 | -1 | -3 | -2 | |||
| -1 | -4 | |||||
С5=1, С4=5, С3=7, С2=2, С1=-4, С0=-2
f(х)= (х-1)5+5(х-1)4+7(х-1)3+2(х-1)2-4(х-1)-2.
****************************************************************
Лекція 2






