Кривая у=ƒ (х) называется выпуклой на интервале, если все точки кривой лежат ниже любой ее касательной на этом интервале. Тогда на этом интервале
ƒ¢¢(х)< 0.
Кривая у=ƒ (х) называется вогнутой на интервале, если все точки кривой лежат выше любой ее касательной на этом интервале. Тогда на этом интервале
ƒ¢¢(х) > 0
Определение. Точкой перегиба кривой называется точка, по одну сторону от которой кривая выпукла, по другую вогнута.
В точке перегиба ƒ ¢¢(х)=0.
Итак, знак второй производной (как и знак самой функции и ее первой производной) свидетельствует об особенностях графика функции. Еще раз остановимся на них.
Если для всех х на интервале (а, b) ƒ (х) > 0 (ƒ (х) <0), то график лежит выше (ниже) оси абсцисс.
Если для всех х на интервале (а, b) ƒ ¢(х) > 0 (ƒ ¢(х) < 0), то функция на (а, b) возрастает (убывает).
Если для всех х на интервале (а, b) ƒ ¢¢(х) > 0 (ƒ ¢¢(х) < 0), то график на (а, b) вогнут (выпукл).
Уравнение ƒ(х)=0 определяет «нули» функции, т. е. точки пересечения графика с осью Ох.
Уравнение ƒ ¢(х)=0 определяет критические точки.
Уравнение ƒ ¢¢(х)=0 определяет возможные точки перегиба.
Схема исследования функции
Для исследования функции ƒ (х) и построения графика у=ƒ (х) следует найти:
1) область определения функции и точки пересечения графика с осями координат;
2) интервалы монотонности;
3) точки экстремумов и значения функции в этих точках;
4) интервалы выпуклости и вогнутости графика;
5) точки перегиба графика;
6) построить в декартовой системе координат все полученные точки (иногда, для уточнения графика, получают дополнительные точки) и сам график.
Наименьшее и наибольшее значения функции на отрезке
При решении некоторых задач метода оптимизации важно уметь находить наименьшее или наибольшее значения функции на некотором отрезке. Эти значения функция достигает либо в критических точках, либо на концах отрезка.
Схема отыскания наименьшего и наибольшего значений функции ƒ (х) на отрезке [ а, b ].
1. Найти производную функции ƒ ¢(х).
2. Найти критические точки из уравнения ƒ ¢(х)=0.
3. Выбрать те критические точки, которые принадлежат данному отрезку [ а, b ] и найти значение функции ƒ (х) в каждой такой точке.
4. Вычислить значения функции ƒ (х) на концах отрезка: ƒ(а) и ƒ(b).
5. Из полученных значений функции выбрать самое большое (наибольшее) и самое малое (наименьшее).
Пример 2.
Найти наибольшее и наименьшее значения функции ƒ(х) = х3–9х2+24х–10 на отрезке [0 3].
1. ƒ ¢(х) = 3 х 2 – 9·2 х 2 + 24.
2. ƒ¢(х)=0, 3(х 2–6 х +8)=0, х 1=2, х 2=4.
3. Точка х2=4 не принадлежит отрезку [0, 3]. Поэтому вычислим значение функции только в точке х 1=2
ƒ(2)=23–9·22+24·2–10=10.
4. Значения функции на концах отрезка: ƒ(0)= –10, ƒ(3)=33–9·32+24·3–10, ƒ(3)=8.
5. Получены значения:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Наибольшее значение равно 10 и достигается в точке х =2. Наименьшее – равно –10 и достигается в точке х =0.
Пример 3.
Найти интервалы выпуклости и вогнутости и точки перегиба кривой у=х +36 х 2–2 х 3– х 4.
Областью определения данной функции является множество всех действительных чисел, т. е. х Є(–∞, +∞).
Найдем вторую производную. у ¢=1+72 х –6 х 2–4 х 3.
у ¢¢=72–12 х –12 х 2= –12(х 2+ х –6).
Из уравнения у ¢¢=0 получим абсциссу точки перегиба: –12(х 2+ х –6)=0 х 1= –3; х 2=2.
Определим знак у ¢¢ на интервалах
(–∞; –3), (–3; 2), (2, +∞).
| х | (–∞, –3) | -3 | (–3; 2) | (2; +∞) | |
| у ¢¢ | – | + | – | ||
| форма кривой | выпукла 
| перегиб | вогнута

| перегиб | выпукла 
|
Найдем ординаты точек перегиба:
у (–3)=726; М 1(–3; 726) – точка перегиба
у (2)=114; М 2(2; 114) – точка перегиба.
На интервале (–3; 2) кривая вогнута. На интервалах (–∞; –3) и (2; +∞) – выпукла.
Пример 4.
Исследовать функцию  и построить ее график.
и построить ее график.
1. Данная функция является многочленом (можно раскрыть скобки, получим многочлен третьей степени), поэтому она определена, непрерывна и дифференцируема при любых х.
2. Найдем производную.
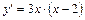 .
.
Из уравнения у¢ =0 найдем критические точки: 3 х ·(х –2)=0, х 1=0, х 2=2. Исследуем их.
| х | (–∞, 0) | (0; 2) | (2; +∞) | ||
| у¢ | + | – | + | ||
   у у
| |||||
| возрастает | max | убывает | min | возрастает |
3. Итак, функция возрастает на интервалах (–∞, 0) и (2, +∞), убывает на интервале (0; 2), имеет максимум при х=0 и минимум при х=2:
у max= у (0)=4; у min= у (2)=0.
4. Найдем вторую производную.
у¢¢= 6·(х -1).
Кривая выпукла там, где у¢¢ < 0, т. е. 6·(х –1) < 0, х < 1.
Кривая вогнута там, где у¢¢ > 0, т. е. х > 1.
Итак, на интервале (–∞, 1) кривая выпукла; а на интервале (1, +∞) – вогнута.
5. Точку перегиба найдем из уравнения у¢¢ =0. Таким образом, х =1 – абсцисса точки перегиба, т.к. эта точка разделяет интервалы выпуклости и вогнутости кривой. Ордината точки перегиба: у (1)=2.
График функции у =(х +1)·(х –2)2 пересекает ось Ох при у =0, т. е. при х = –1 и х =2;
пересекает ось Оу при х =0, т. е. при у =4. Мы получили три точки: (–1; 0), (2; 0), (0; 4).
Все полученные точки внесем в таблицу, добавив соседние с ними.
| х | –2 | –1 | 
| 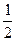
| 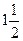
| 
| ||||
| у | –16 | 3 
| 
| 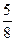
| 
| |||||
| max | перегиб | min |
 |
Рис. 28 Кривая у=(х+1)(х–2)2.






