Кратко остановимся на основных классах элементарных функций, т. к. все они изучаются в курсе средней школы.
Постоянная функция:
ƒ(х)= с.
График ее – прямая у=с.
Степенная функция:
ƒ(х)= х n,
где n – любое число.
При n четном степенная функция является четной, при n – нечетном – функция нечетная.
Приведем графики функций
 |
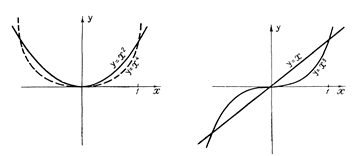ƒ(х)= х, ƒ(х)= х 2, ƒ(х)= х 3, ƒ(х)= х 4.
Рис. 2. Графики степенных функций
Многочлен (целая рациональная функция):
ƒ(х)= а 0+ а 1 х + а 2 х 2+ а 3 х 3+ … + а n х n.
Частные случаи этой функции – хорошо известные линейная функция ƒ(х)= ах + b (график ее – прямая) и квадратный трехчлен ƒ(х)= ах 2+ bх + с (график ее – парабола).
 |
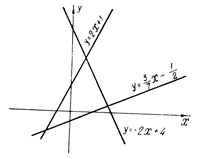Рис. 3. Графики линейных функций
 |
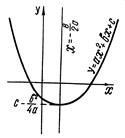Рис. 4. График квадратного трехчлена у=ах2+bх+с, а > 0.
Дробно-линейная функция:
ƒ(х)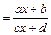 
. Частным случаем этой функции является обратная пропорциональная зависимость, графиком которой является гипербола 
.
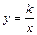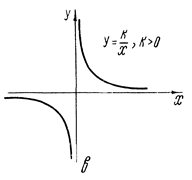
Рис. 5. График дробно-линейной функции.
Показательная функция:
ƒ(х)= а х, а >0, а ¹1.
Эта функция возрастает при а > 1, убывает при 0 < а <1.
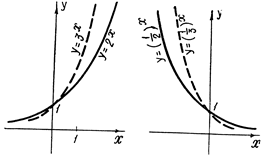
Рис. 6. Графики показательных функций.
Логарифмическая функция:
ƒ(х)=loga x, a > 0, а ¹1
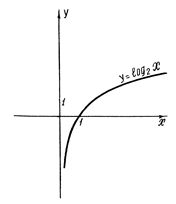
Рис. 7 График логарифмической функции.
Тригонометрические функции
хорошо известны. Приведем их графики
у=sin x, y=cos x, y=tg x, y=ctg x.
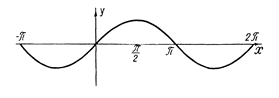
Рис. 8. График y=sin x..
Рис. 9. График у=cos x.
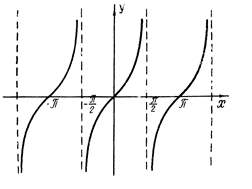
Рис. 10. График у=tg x.
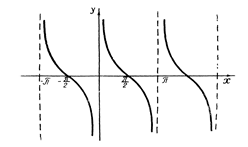
Рис. 11. График у=ctg x.
Обратные тригонометрические функции.
Графики этих функций
y=arcsin x, y=arсcos x, y=arсtg x и y=arcctg x
приведены ниже.
 |
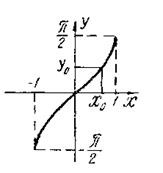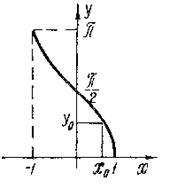
Рис. 12. График функции у=arcsin x
 |
 |
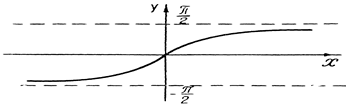Рис. 13. График функции у=arccos x
Рис. 14. График функции у= arctg x
 |
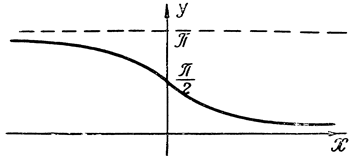Рис. 15. График функции у=arcctg x
Все рассмотренные функции называют основными (или простейшими) элементарными функциями.
Рассмотрим сложные функции. Пусть функция у =ƒ(х) определена на множестве Х со значениями на множестве У. Пусть на множестве У задана функция z=φ (у), которая всякому значению х из Х сопоставляет значение переменной z, полученное через промежуточное значение переменной у. Поэтому z -функция переменной х:
z=φ (ƒ(х)),
с областью определения Х, но зависимость z от х осуществляется через посредство переменной у, которая называется промежуточным аргументом. Итак, переменная z здесь – функция от функции. Функцию такого рода называют сложной функцией (или суперпозицией функций).
Функции, записываемые с помощью конечного числа суперпозиций основных элементарных функций, называют элементарными функциями.
Примеры элементарных функций:
у =lg tg x,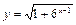 
, y =(1+ cos 23 x)3.
Понятно, что чаще приходится иметь дело именно с элементарными функциями.
