Понятие функции и функциональной зависимости является основополагающим в математике. Это понятие тесно связано с понятием числового множества.
Числовым множеством будем называть всякую совокупность вещественных чисел. Каждое вещественное число изображается точкой числовой оси, поэтому всякому числовому множеству можно сопоставить на оси множество точек.
Отрезком [ а, b ] называется множество чисел х, для которых а £ х £ b. Длина отрезка [ а, b ] равна b – а.
Интервалом (а, b) называется множество чисел х, для которых а < x < b.
Интервал называют открытым промежутком, отрезок – замкнутым.
Дадим важное в дальнейшем понятие δ-окрестности (δ – дэльта) точки. Пусть х 0 – некоторое число и δ > 0 (положительное число).
Определение. δ-окрестностью числа х 0 называется множество чисел х, удовлетворяющих неравенству х 0– δ < х < х 0+ δ.
 |
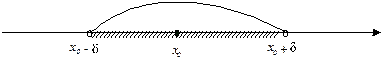Иначе говоря, δ -окрестность точки х 0 – это интервал с центром в точке х 0, длина которого равна 2 δ.
Рис. 1.
Используя определение модуля (абсолютной величины) числа, δ -окрестностью числа х 0 можно назвать все те числа х, которые удовлетворяют неравенству | х – х 0|< δ.
Изучая тот или иной процесс, мы сталкиваемся с различными величинами, которые можно разбить на два типа.
Одни величины в данном процессе остаются неизменными. Их называют постоянными величинами. Другие в данном процессе изменяются и называются переменными. Например, при движении автомобиля его длина, ширина постоянны, а длина пути, количество бензина в баке являются величинами переменными.
Определение. Множество всех значений переменной величины, которое она принимает в процессе своего изменения, называется множеством ее значений или областью изменения переменной.
Рассматривая некоторый процесс, мы имеем дело со взаимным изменением нескольких величин, когда изменение одной величины влечет изменение другой.
Понятие функциональной зависимости возникло в результате отвлечения от физической сущности взаимно изменяющихся величин и выделения самого факта зависимости.
Определение. Если каждому значению переменной величины х из множества Х ее значений по некоторому правилу сопоставлено определенное значение другой переменной у, то у называется зависимой переменной или функцией от х.
х называется независимой переменной (аргументом); множество Х называется областью определения данной функции. Множество У значений переменной у называется множеством значений функции.
Задать функцию – значит задать и область определения ее и закон соответствия между переменными х и у.
Функция обозначается следующим образом: у=ƒ(x), y=φ( х), у = F (х) и т.п.
Способы задания функции
Аналитический способ задания является одним из самых распространенных и наилучшим образом приспособлен к операциям математического анализа. Функциональная зависимость задается с помощью формулы, аналитического выражения.
Например,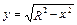 
. Здесь функция у принимает только неотрицательные значения и определена на множестве, где R 2– х 2 ³ 0, т.е. х 2£ R 2. Если R >0, то – R £ x £ R.
Другой пример: 
.
Здесь у – функция, определенная всюду (х – любое число), и принимает любые действительные значения.
Заметим, что к недостаткам аналитического способа следует отнести следующее: не всякую функциональную зависимость можно задать аналитически, найденная формула может быть очень громоздкой и неудобной для исследования, наконец, формула не дает наглядности.
Табличный способ задания знаком из школьного курса (таблицы значений для sinx, cosx, lgx, …). При табличном способе задания выбирается лишь ограниченное число значений аргумента х, и соответствующие им значения функции у заносятся в таблицу.
Недостатком этого способа задания прежде всего является то, что некоторых нужных нам значений функции в таблице может не быть.
Рассмотрим наиболее наглядный способ задания функции.
График и графическое задание функции
В прямоугольной системе координат на плоскости построим множество точек М (х, у), где у =ƒ(х). Полученное множество называется графиком функции ƒ(х). В этом случае уравнение у =ƒ(х) называют уравнением множества точек М.
Как правило, будем рассматривать функции, график которых состоит из одной линии или из совокупности нескольких линий.
График является наглядным и легко обозримым изображением функции и поэтому оказывает большую помощь при изучении ее.
Рассмотрим некоторые общие свойства функций.
Ограниченность функции
Назовем функцию ƒ(х) ограниченной, если для всех х из области ее определения существует такое число D, что |ƒ (х)| < D (D >0).
Например, функции sin x и cos x являются ограниченными.
Монотонные функции
Функция ƒ (х) называется возрастающей в области ее определения Х, если бóльшим значениям аргумента соответствуют и бóльшие значения функции, т. е. для х 1 < х 2 ƒ(х 1) < ƒ(х 2).
Функция ƒ(х) называется убывающей, если для х 1 < х 2 ƒ(х 1) > ƒ (х 2).
Например, функция ƒ(х)=2х является возрастающей.
Возрастающие и убывающие функции называются монотонными.
Периодические функции
Функция ƒ(х) называется периодической с периодом Т, если равенство
ƒ(х +Т)=ƒ(х)
выполняется для всех х из области определения функции.
Например, sin (х +2π)= sin x, tg (x +π)= tg x. Это значит, что функция sin x – периодическая с периодом 2π, tg х – периодическая с периодом π.
Четные и нечетные функции
Функция ƒ(х) должна быть определена в симметричной относительно начала координат области.
Функция ƒ(х) называется четной, если значение не изменится при замене х на – х, т. е.
ƒ(– х)=ƒ(х).
Если же ƒ(– х)= –ƒ(х), то ƒ(х) – нечетная. Например, х 2, х 4, cos x, 1+5· x 2 – функции четные,
х, х 3, sin x, tg x – функции нечетные.
Заметим, что график четной функции симметричен относительно оси ординат Оу, а график нечетной функции симметричен относительно начала координат.
