Пустьфункция у =ƒ(х) определена в некоторой области Х и х 0 – точка внутри Х. Перейдем из точки х 0 в другую точку области Х, изменив значение х 0 на величину Δ х (говорят: дадим х 0 приращение Δх). Эта другая точка х=х0 +Δ х. Функция ƒ(х) при этом тоже получит некоторое приращение
Δу =Δƒ(х 0)=ƒ(х 0+ Δх)–ƒ(х 0).
Приращение функции Δƒ(х 0) (или Δу) – величина, на которую изменяется значение функции, когда аргумент получает приращение Δх.
Основным вопросом, который нас будет интересовать, является вопрос о характере изменения функции в точке х 0. Точнее, нас будет интересовать скорость изменения значений функции при переходе от значения х 0 независимой переменной к другому.
Рассмотрим для этого отношение приращения функции к приращению независимой переменной
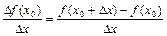
Это отношение называют средней скоростью изменения функции на промежутке между точками х0 и х0+Δх.
Средняя скорость зависит от Δх, поэтому средняя скорость не будет достаточно хорошей характеристикой изменения функции в точке х 0. За скорость изменения функции ƒ(х) в точке х 0 принимается предел средней скорости при Δ х ®0.
Определение. Если существует конечный предел отношения приращения
функции у =ƒ(х) к приращению независимой
переменной, когда это приращение стремится к нулю, то
этот предел называется производной функции у =ƒ(х) в
точке х 0и обозначается одним из следующих символов:
, 
.
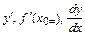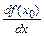По определению: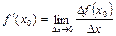 
или 
.
Таким образом, производная ƒ¢(х0) есть скорость изменения функции ƒ(х) в точке х0. Таков физический смысл производной.
Рассмотрим геометрический смысл производной.
Пусть дан график функции у =ƒ(х), представляющий собой некоторую кривую. Отметим на ней некоторую точку М0. Если М – другая точка этой кривой, то прямая М0М называется секущей.
Определение. Касательной к кривой в точке М0 называется предельное
положение секущей М0М при условии, что точка М, двигаясь по кривой, приближается к точке М0.
 |
Рис. 22.
Пусть х 0 и х0+Δх – абсциссы точек М0 и М графика функции у =ƒ(х). Ординатами этих точек будут числа ƒ(х 0) и ƒ(х0+Δх) или у 0=ƒ(х 0) и у0+Δу =ƒ(х0+Δх).
Запишем уравнение касательной к графику у =ƒ(х) в точке М0 (х0, у0):
у–у0=k·(х–х0),
где k – угловой коэффициент касательной, т. е. k=tg α.
Поскольку касательная – предельное положение секущей, то и угол α наклона касательной есть предел угла β наклона секущей, т. е. k=tg α=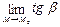 
, при условии, что точка М по графику приближается к точке М0, но тогда Δ х ®0.
Из треугольника М0FМ 
и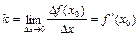 
.
Таким образом, касательная к графику функции у=ƒ(х) существует, если в точке х 0 функция ƒ(х) имеет производную, а угловой коэффициент касательной в точке М0 (х0, у0) равен значению производной в точке х0, т. е. k =ƒ¢(x 0).
Уравнение касательной: у–у0=ƒ¢(х0)·(х–х0).
Выяснив физический и геометрический смысл производной, рассмотрим основные свойства и формулы дифференцирования (дифференцированием функции называется процесс отыскания ее производной).
Теорема 1. Если функция ƒ(х) дифференцируема в точке х 0, то ƒ(х)
непрерывна в точке х 0.
Заметим сразу, что обратное утверждение не всегда верно.
Теорема 2. Если функция ƒ(х) во всех точках отрезка [ а, b ] имеет
положительную производную, то ƒ(х) возрастает на [ а, b ],
т. е. еслиƒ¢(х) > 0 на [ а, b ], то ƒ(х) возрастает на [ а, b ].
Теорема 3. Если функция ƒ(х) во всех точках отрезка [ а, b ] имеет
отрицательную производную, то ƒ(х) убывает на [ а, b ], т. е.
 |  | ||
е сли ƒ¢(х) < 0, то ƒ(х) убывает на [ а, b ].
Рис. 23. Рис. 24.
В случае ƒ¢(х) > 0 и tg α > 0, т. е. в любой точке графика угол наклона α < 900. Функция возрастает на [ а, b ].
В случае ƒ¢(х) < 0 tg α < 0 и угол наклона касательной α > 900. Функция убывает на [ а, b ].
Теоремы 2 и 3 используются при решении задачи на отыскание интервалов монотонности функции.
